Қазақстан Білім және Ғылым министрлігі

Л.Н. Гумилев атындағы Еуразия Ұлттық Университеті

РЕФЕРАТ

Тақырыбы: Үш еселі интеграл

Орындаған: Маркленов А. Е. РЭТ – 15 топ

Тексерген: Баймадиева Ғ. Ә.

Астана 2013 ж.

Үш еселі интегралдың анықтамасы және қасиеттері

 

XYZ кеңістігінде V кубталатын тұйық облысында кез келген функция берілсін. V облысын ортақ ішкі нүктелері болмайтын n облыстарға бөлейік. облыстарынының әрбірінен нүктелерін аламыз. функциясының нүктелеріндегі мәндерін көлемдеріне көбейтіп, осындай көбейткіштерді қосамыз. Алынған қосынды функциясы үшін V облысы бойынша интегралдық қосынды деп аталады. функциясы үшін V облысы бойынша шексіз интегралдық қосынды құруға болады.

Егер V облысында бөлу қадамы нөлге ұмтылғанда интегралдық қосындының шегі бар болса, онда бұл шек функциясының V облысы бойынша үш еселі интеграл деп аталады және оны

немесе

символымен белгілейді.

Мұндағы - интеграл астындағы функция, V – интегралдау облысы, x, y және z – интегралдау айнымалылары, - көлем элементі.

Үш еселі интегралдар екі еселі интегралдардың үш өлшемді кеңістіктегі жалпы жағдайы.

Теорема 1. Егер функциясы V тұйық облысында үзіліссіз болса, онда үш еселі интеграл бар болады.

Үш еселі интегралдың геометриялық мағынасы: V дененің көлемін үш еселі интеграл арқылы есептеуге болады

Үш еселі интегралдың механикалық мағынасы: V дененің массасы

формуласымен анықталады, мұндағы - масса тығыздығы.

Үш еселі интегралдың негізгі қасиеттері:

1. Үш еселі интеграл интегралдау айнымалыларын белгілеуден тәуелді емес, яғни

2. Тұрақты көбейткішті үш еселі интеграл таңбасының алдына шығаруға болады:

мұндағы k – сан.

3. Екі функция қосындысының үш еселі интегралы осы функциялардың үш еселі интегралдарының қосындысына тең:

4. Егер V облысы екі V1 және V2 облыстарына бөлінсе, онда

5. Егер V облысында

6. Егер V облысында

онда

7.

Үш еселі интегралды есептеу жолдары

 

Теорема 1. V облысы төменнен және жоғарыдан және беттерімен шектелген болсын, мұндағы және - XOY жазықтығындағы тұйық облысында үзіліссіз функциялар. Онда V тұйық облысындағы кез келген үзіліссіз функциясы үшін келесі формула орындалады

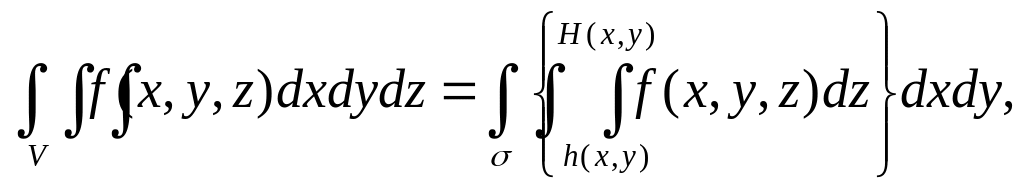(1)

Бұл формула үш еселі интегралды анықталған интегралдың екі еселі интегралына әкеледі.

Теңдіктің оң жағындағы интеграл келесі түрде жазылады:

Үш еселі интегралды (1) формуласы бойынша есептегенде алдымен z айнымалысы бойынша (x және y- тұрақтылар) ішкі интеграл есептеледі, одан кейін x және y бойынша облысында екі еселі интеграл есептеледі.

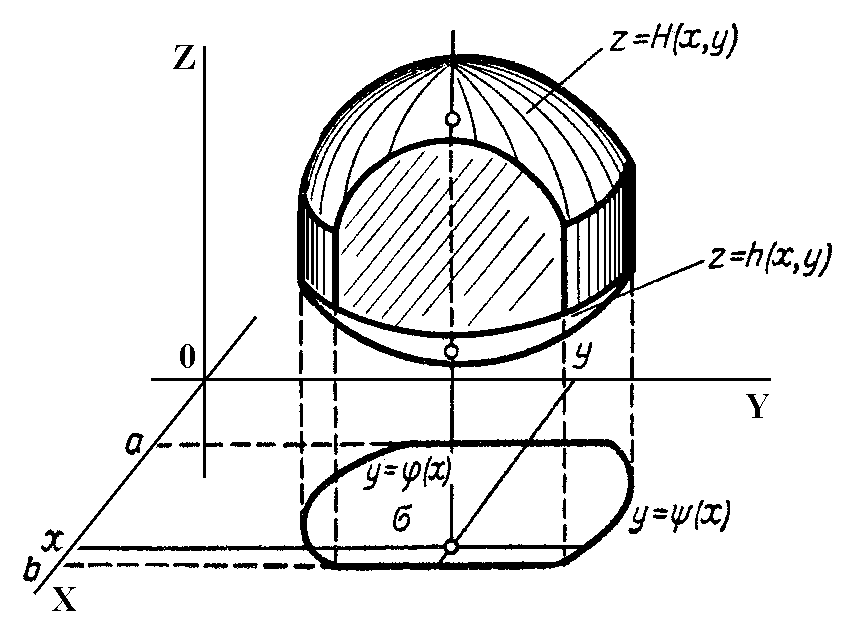
сурет 4.13.1

Егер облысы XOY жазықтығында x=a, y=b (a<b), сызықтарымен шектелсе, [ және [а, b] кесіндісінде үзіліссіз функциялар , сонымен қатар (сурет 4.13.1.)], онда екі еселі интгералдан облысы бойынша қайталанбалы интегралға көшіп

(2)

формуласын аламыз.

Егер V облысы - x=a, x=b (a<b), y=c, y=d (c<d), z=l, z=k (l<k) жазықтықтарымен шектелген параллелепипед болса, онда (2) формуласы:

Егер функциясы әрқайсысы бір ғана айнымалыдан тәуелді үш функцияның көбейтіндісі болса,

онда V параллелепипеді бойынша үш еселі интеграл осы функциялардың анықталған интегралдарының көбейтіндісіне тең.

сурет 4.13.2 сурет 4.13.3

Мысал 1. x = -1, x = +1, y = 0, y = 1, z = 0, z = 2 жазықтықтарымен шектелген параллелепипед бойынша үш еселі интегралын есептеңіз. (2) формуласы бойынша:

Мысал 2. жазықтықтармен шектелген V облысы бойынша үш еселі интегралды есептеңіз(сурет 4.13.3.).

V облысы XOY жазықтығына түзулерімен шектелген үшбұрышы болып проекцияланады. 1 және 2 формулаларын қолданамыз:

Үш еселі интегралдың кейбір механикалық қолданулары

 Егер XYZ кеңістігінде V облысының масса тығыздығы белгілі болса, онда V облысына байланысты статикалық моменттер келесі формулалармен есептеледі:

Координат өстеріне қатысты инерция моменттері:

Ауырлық центрінің координаттары:

 2.4 Үш еселі интегралда айнымалыны ауыстыру

 Егер функциясы V тұйық облысында үзіліссіз болса, ал

(1)

функцияларының UVW кеңістігіндегі Т тұйық облысында үзіліссіз дербес туындылары бар болып және осы облысты XYZ кеңістігіндегі V облысына бірмәнді бейнелесе, онда келесі теңдік орындалады:

(2)

мұндағы - якобиан бейнелеуі

сурет 4.16.1

Үш еселі интегралда цилиндрлік координаталарға көшу

 XYZ кеңістігіндегі нүктесінің орны үш санды белгілеуден бірмәнді анықталады, мұндағы - М нүктесінің XOY жазықтығындағы проекциясы радиус-вектордың ұзындығы, - OX өсімен радиус-вектор арасындағы бұрыш, z – М нүктесінің аппликатасы. Олар М нүктесінің декарттық координаталарымен келесі қатынастар арқылы байланысады:

(1)

Анықтама бойынша , .

Якобиан бейнелеуі:

берілген жолақта теріс емес ( жолақтың шекарасында ғана).

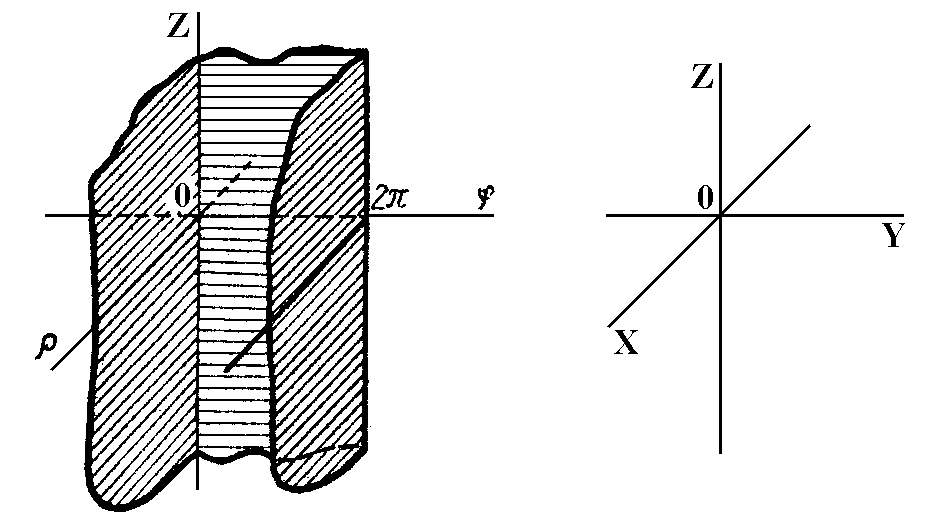
сурет 4.16.2

(1) формуласын үш еселі интегралға қолдану үш еселі интегралда декарттық координатадан цилиндрлік координатаға көшу формуласы деп аталады:

Мұнда Т – (1) формуласы арқылы V облысынының кеңістігіндегі бейнеленген облысы.

Мысалы. беттерімен шектелген дененің V көлемін цилиндрлік координата арқылы есептеңіз.

Т арқылы беттерімен шектелген кеңістігінің облысын белгілейміз (сурет 4.16.4.).

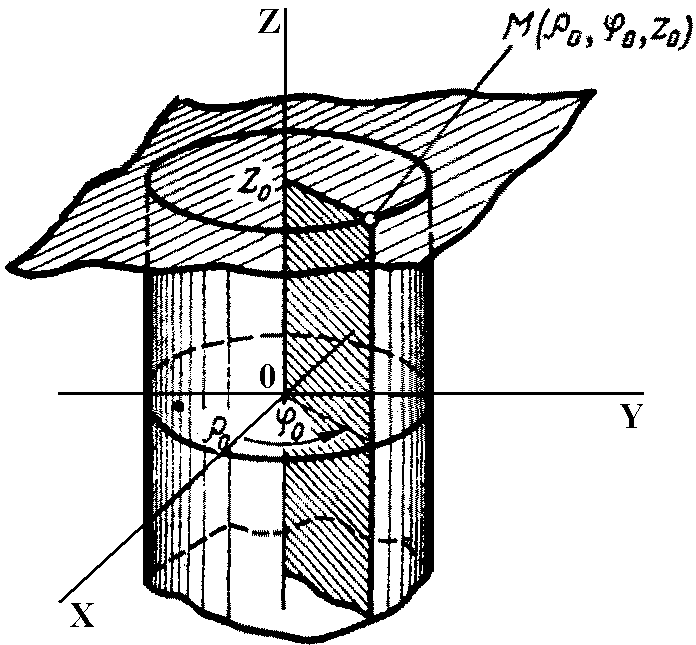
сурет 4.16.3

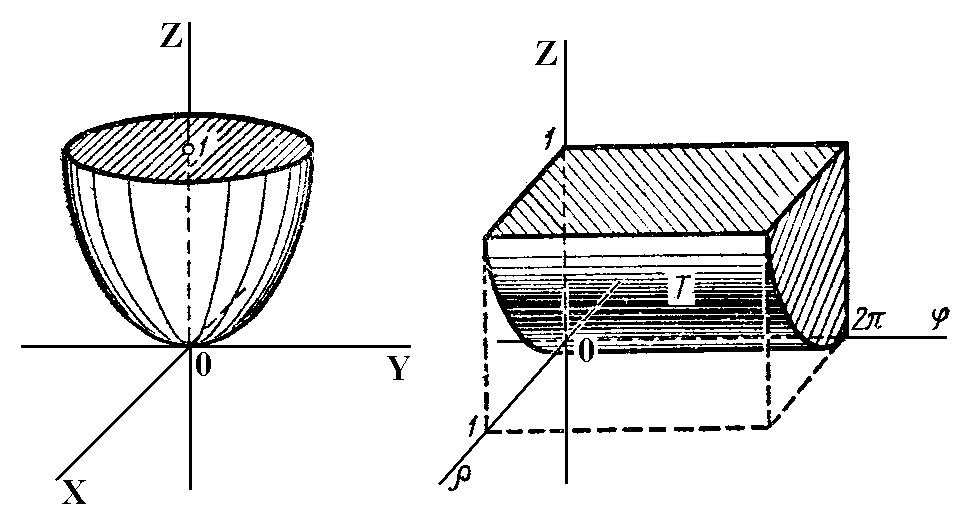
сурет 4.16.4