Метод минимального риска

Найдём граничное значение x0 из условия минимума среднего риска.

Дифференцируя уравнение среднего риска (*) по х0 и приравнивая производную к 0 получим условие экстремума

dR/dx0=C11P1 f(x0/D1)-C21P1f(x0/D1)+ C12P2f(x0/D2)-C22P2f(x0/D2)=0

или

f(x0/D1)/f(x0/D2)=(C12-C22)P2/((C21-C1)P1)

Для существования минимума R в точке x=x0 вторая производная должна быть .

Это даёт нам следующее:

f'(x0/D1)/f'(x0/D2)<(С12-С22)P2/((C21-C11)P1

Лекция 16.11.2012

Величина

представляет собой пороговое значение для отношения правдоподобия. В большинстве практических задач условные выигрыши для правильных решений не вводятся. Тогда 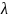будет равно

=P2 C12 / (P1 C21)

Старое правило решения

При x<x0 K D1

При x>x0 K D2

в данном случае выражается в форме отношения правдоподобия и для принятия решения даже не требуется определение критического параметра x0. Это справедливо при достаточно плавных одногорбых распределениях.

Перепишем по-другому функцию риска R

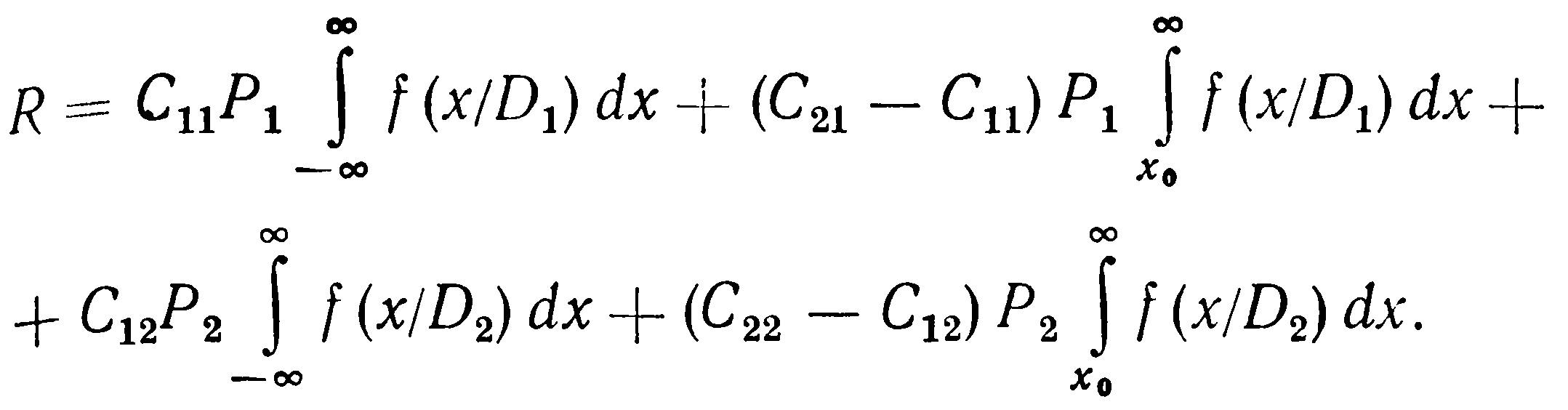
Учитывая

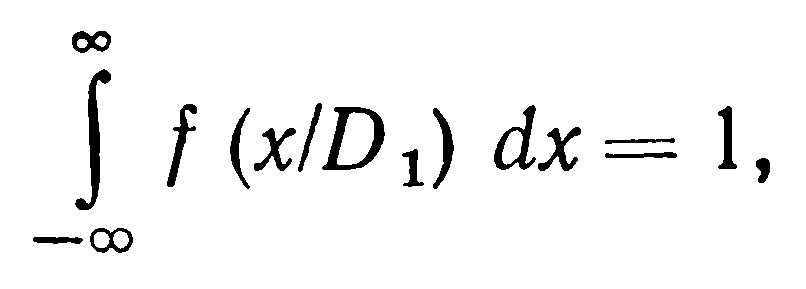
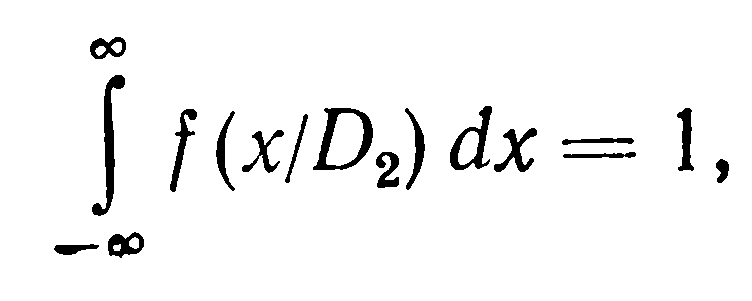
получим

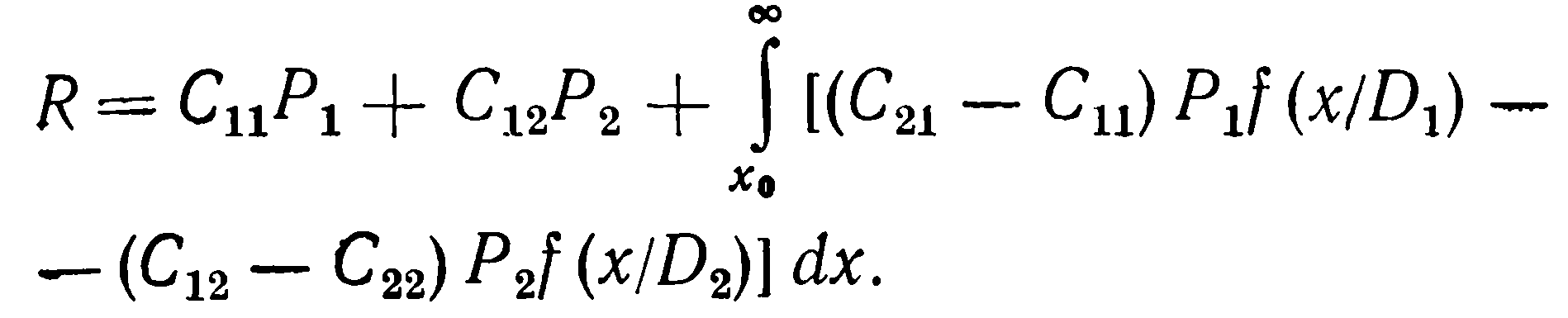
Найдём минимум

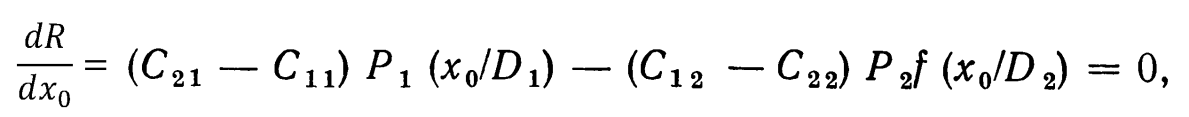
или

Правило решения остаётся прежним и остаются в силе услвия 1 и 2.

Надёжность и отказоустойчивость

Под надёжностью и безопасностью систем управления понимается её защищённость от случайных или преднамеренных вмешательств в нормальный процесс её функционирования. К таким вмешательствам можно отнести:

1. Отказы и сбои в электрических схемах

2. Ошибки в программировании

3. Аварийные ситуации

НТС определяется свойствами:

1. Безотказность

2. Работоспособность

3. Долговечность

4. Сохраняемость

5. Ремонтопригодность

Работоспособность – состояние системы, при котором оно нормально выполняет заданные функции в соответствии с технической документацией.

Ремонтопригодность – приспособленность системы к предупреждению, обнаружению и ликвидации отказов.

Отказ – событие, заключающееся в полной или частичной потере работоспособности.

Классификация отказов:

1. По характеру изменения параметра до момента возникновения отказа

2. По связи с другими отказами

   1. Независимый отказ

   2. Зависимый отказ

3. По возможности последующего использования

   1. Полный отказ

   2. Частичный отказ

4. По характеру устранения отказа

   1. Устойчивый отказ

   2. Самоустраняющийся отказ

5. По наличию внешнего проявления

   1. Очевидный (явный) отказ

   2. Неочевидный (неявный) отказ

Лекция 19.11.2012

6. По причине возникновения

   1. Конструктивный отказ

   2. Технологический

   3. эксплуатационный

7. по причине происхождения

   1. естественный

   2. искусственный

8. по времени возникновения отказа

   1. отказ при испытании

   2. отказ в период нормальной эксплуатации

   3. отказ после эксплуатации

Показатели надёжности систем управления

Функционирование АСУ – чередование интервалов работоспособности и отказов. Продолжительность этих интервалов – величина случайная. Поэтому для описания показателей надёжности АС используют математический аппарат теории вероятностей, теории случайных процессов и математической статистики.

1. Показатель безотказности

Вероятность того, что наработка 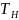между отказами превзойдёт заданное время T.

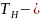время наработки

Один из показателей безотказности – вероятность безотказной работы системы P(t), т.е. вероятность того, что в течении времени (наработки) t не будет ни одного отказа. Часто представляется в виде

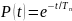
2. Показатель ремонтопригодности

   1. Вероятность 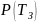восстановления системы за заданное время

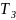
   2. Среднее время восстановления системы

   3. Коэффициент технического использования – отношение времени наработки на отказ к средней продолжительности цикла «работа-восстановление-профилактика»

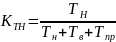
3. Показатели сохраняемости

Даёт количественную характеристику способности системы сохранят своё качество при транспортировке и хранении.

1. Средний срок сохраняемости – среднее время хранения, в течении которого изменение параметров системы или её элементов не превышают допустимых

Вероятность безотказной работы системы зависит от безотказной работы элементов системы 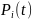и определяется по формуле

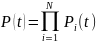
где N – количество элементов.