Структура технической диагностики

Техническая диагностика:

1. Теория распознавания

• Алгоритмы распознавания

• Правила решения

• Диагностика модели

2. Теория контролеспособности

• Контроль состояния

• Поиск неисправности

• Средства и методы получения диагностической информации

Лекция 19.10.2012 Классификация систем диагностики

1. По степени общности даваемой информации

   1. Локальные, т.е. оценка состояния узлов и деталей

   2. Общие, т.е. диагностика в целом

2. По характеру взаимодействия с объектом

   1. Тестовые – формирование воздействия и исследование отклика на это воздействие

   2. Функциональные – регистрируют информацию об объекте в процессе функционирования

В случае создания автоматизированной системы диагностирования необходимо решить следующие задачи:

1. Разработка мат. модели функционирования объекта

2. Разработка мат. модели повреждений и отказов

3. Разработка алгоритмов для диагностирования в соответствии с поставленной задачей – обнаружение неисправностей и отказов, отличие неисправного оборудования от работоспособного, поиск места дефекта

Цели технической диагностики

Основная цель – повышение ресурса и надёжности технических систем для обеспечения отсутствия отказов во время функционирования.

Дальше пропущено 4 листа по диагностике (вопросы 21-24)

Лекция 22.10.2012

Отсутствие признака K1

Отсутствие приз.

Теперь вычислим вероятность для случая, когда оба признака отсутствуют.

Формула для события

Для отсутствия и наличия :

0,05*0,8*0,3/…

Метод последовательного анализа

Предложен учёным Вальдом. Применяется для дифференциальной диагностики (распознавания двух состояний). В отличии от метода Баеса, число обследований заранее не устанавливается, их проводится столько, сколько необходимо для принятия решения с определённой степенью риска.

При использовании метода Баеса для распознаваний состояний D1 и D2 следует составить соотношение

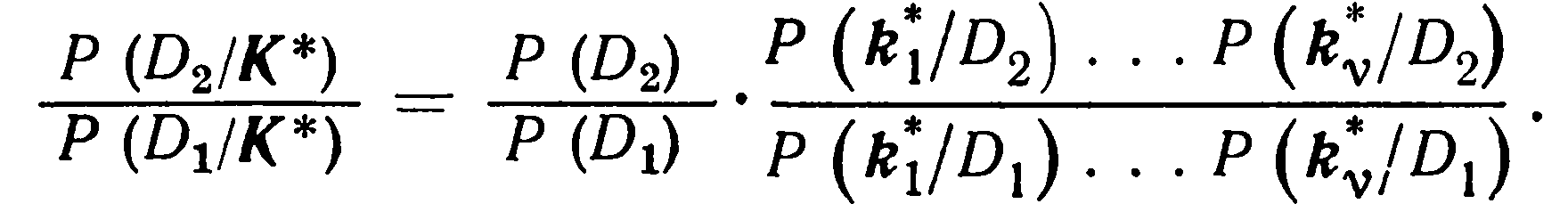
Если

Или

то принимается решение .

В методе последовательного анализа рассматриваемые отношения вероятностей признаков (отношения правдоподобия) составляются не сразу, а в последовательном порядке, поэтому обычно требуется меньшее число обследований.

Пример: Пусть при диагнозе D1 Признак k1 встречается с вероятностью . Соответственно отсутствует с вероятностью .

Если у объекта состояние K* наблюдается признак K1 значительно чаще, при диагнозе D2, чем при диагнозе D1, то можно сделать вывод в пользу диагноза D2.

где A – верхняя граница принятия решения.

В противоположном случае, когда признак K1 значительно чаще встречается при диагнозе D1, принимается решение в пользу диагноза D1.

P(K1/D2)/P(K1/D1) <B

Если B< P(K1/D2)/P(K1/D1) <A, то для решения требуется поступление доказательной информации, проводится обследование по признаку K2 и составляется произведение двух отношений правдоподобия

Методы статистических решений для одного диагностического параметра

Пусть производится диагностика состояния какого-либо объекта по параметру x. Задача состоит в выборе x0 таким образом, что при x>x0 следует принимать решение о снятии двигателя с эксплуатации, а при x<x0 допускать дальнейшую работу. D1 – исправен; D2 – дефект.

При x<x0 K D1

При x>x0 K D2

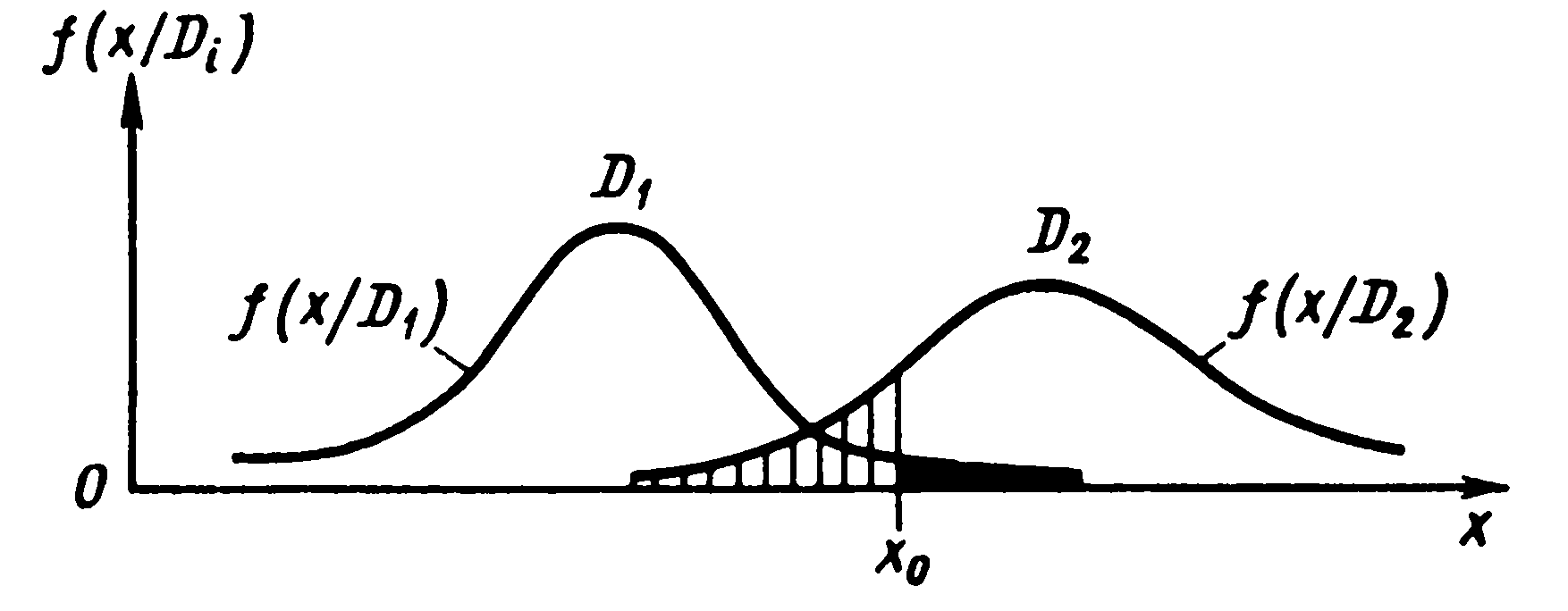
Области исправного и дефектного состояния D1 и D2 пересекаются, поэтому невозможно выбрать значения x0 при котором решающее правило не давало бы ошибочных решений. Задача состоит в том, чтобы x0 был в каком то роде оптимальным, например давал бы минимальное число ошибочных решений.

Введём понятия:

1) «ложная тревога»: случай, когда применяется решение о наличии дефекта, но в действительности система находится в исправном состоянии (вместо D1 принимается D2).

2) «пропуск цели» (дефекта) – принятие решения об исправном состоянии, тогда как система содержит дефект (вместо D2 принимается D1)

Введём обозначение , где первый индекс – номер принятого значения, второй индекс – действительное состояние.

Тогда H12 – пропуск дефекта, H21 – ложная тревога.

H11 и H22 – это правильные решения.

Рассмотрим вероятность P(H21).

Вероятность ложной тревоги равна вероятности произведения двух событий: «наличие исправного состояния» и «x>x0»

Вероятность того, что событие D1 умножить на то, что мы приняли, что сейчас событие D2:

P(H21)=P(D1)*P(x>x0/D1)

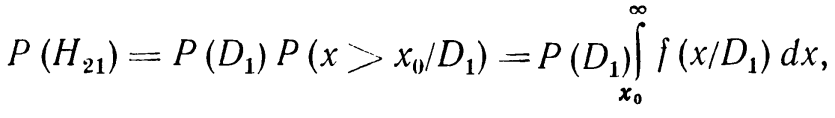
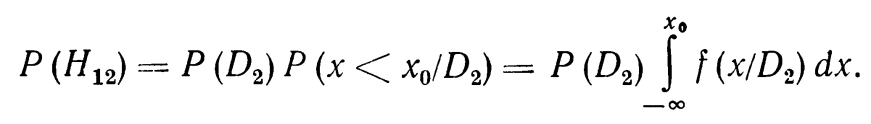
Т.е. вер того что x>x0 при D1 это правая половинка заштрихованной площади.

Средний риск – вероятность принятия ошибочного решения слагается из вероятностей ложной тревоги и пропуска дефекта. Если приписать «цены» этим ошибкам, то получим выражение для среднего риска

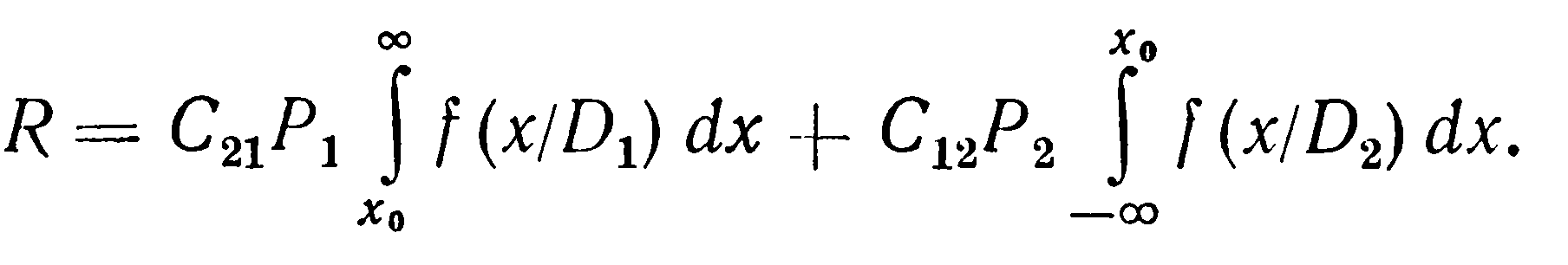
Обычно принимается С12>>С21, т.к. стоимость пропуска дефекта существенно больше стоимости ложной тревоги.

Ингода вводится цена правильных решений H11 и H22, тогда

(*)

С11 и С22 принимаются отрицательными.