Метод Симою

Позволяет определить ПФ по кривой разгона в общем виде, а именно:

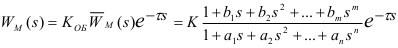
нормированная ПФ, с

Основной задачей является определение коэффициентов c помощью метода М.П. Симою.

Для определения коэффициентов кривая разгона преобразуется к растчётной

Имеет место 2 случая:

• Объект с самовыравниванием

• Объект без самовыравнивания

Лекция 17.09.2012 Объект с самовыравниванием

Кривая разгона при подаче ступенчатого воздействия

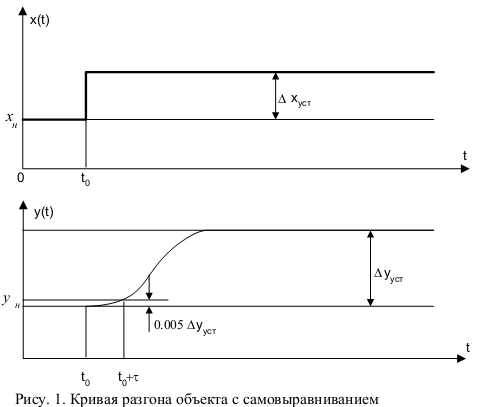
Для получения кривой разгона устанавливается номинальный статический режим, при котором и далее входная величина изменяется на некоторое значение . Запаздывание определяют по графику как время, за которое выходная величина сохраняет номинальное значение.

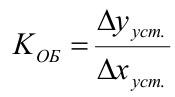
Для расчёта параметров модели методом площадей целесообразно ввести нормированную кривую разгона, которая определяется из соотношения

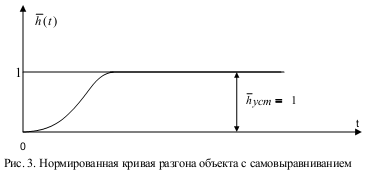
Объект без самовыравнивания

Модель объекта представляется как параллельное соединение некоторого интегрирующего звена и некоторого звена (самовыравнивание).

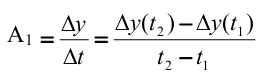
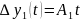(1)

Коэффициент наклона касательной определяется из уравнения прямой (1), где .

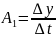Введём функцию

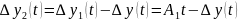
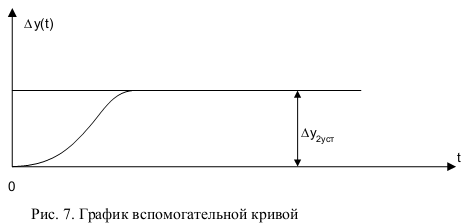
График представляет собой реакцию некоторого объекта с самовыравниванием на скачкообразное изменение входного сигнала .

Тогда передаточную функцию такого объекта можно записать как

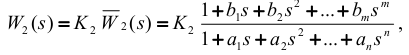
где

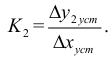
Передаточная функция объекта без самовыравнивания имеет следующий вид

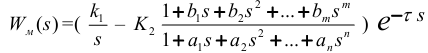
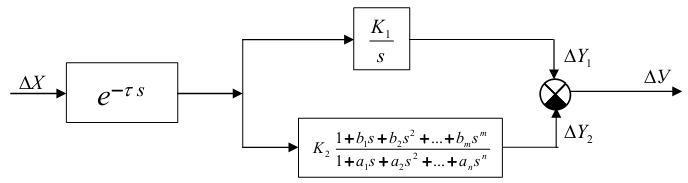
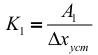
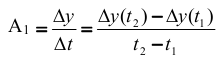
Определение параметров модели по площадям

Рассмотрим инверсную ПФ:

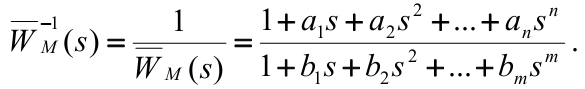
Разложим в ряд Тейлора:

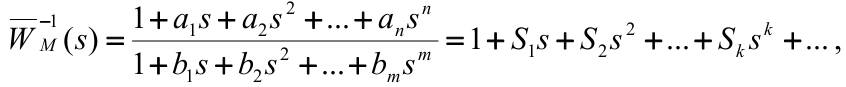
где

Коэффициенты 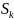названы М.П. Симою площадями.

При известных площадях S легко определить коэффициенты .

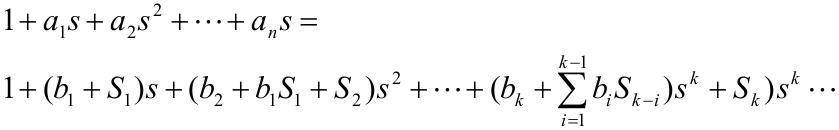
Приравнивая в последнем равенстве коэффициенты при одинаковых степенях s получим линейную систему уравнений для определения параметров a и b.

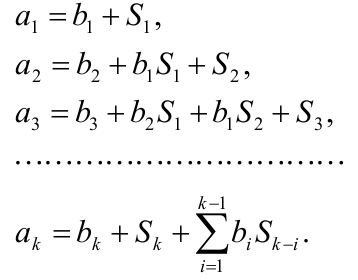
Для определения коэффициентов a и b необходимо число уравнений , где порядок числителя и знаменателя ПФ.

Частный случай:

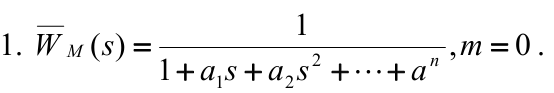
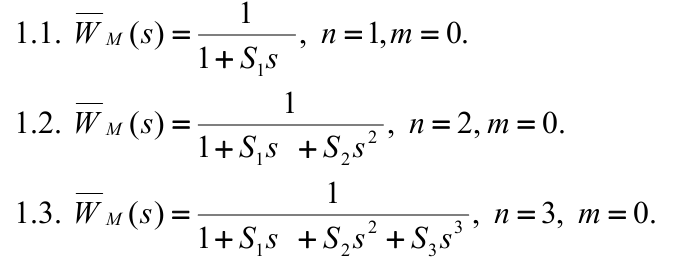
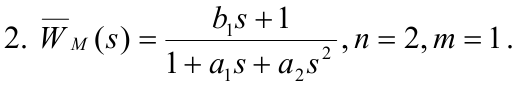
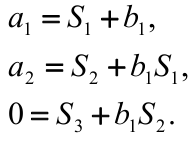
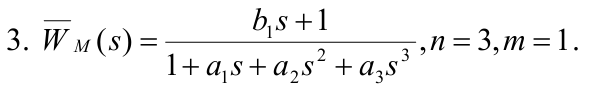
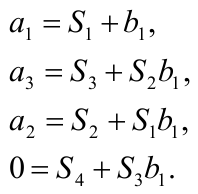
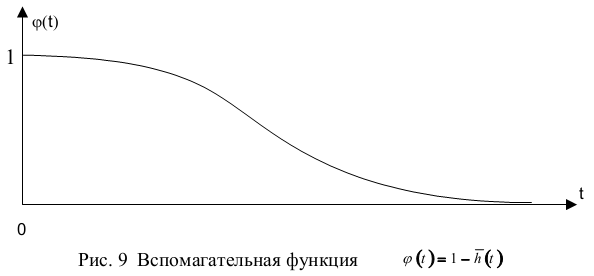
Определение площадей по переходной кривой

Введем в рассмотрение вспомогательную функцию ϕ(t) ( рис.9) определяемую формулой

Определим изображение по Лапласу ϕ(t). Принимая во внимание формулу (6) получим

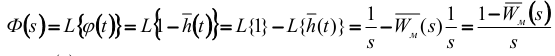
Разложим 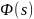в ряд по степеням s в точке s =0:

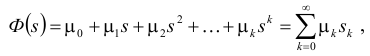
где

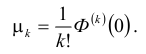
Коэффициенты разложения называются моментами вспомогательной функции ϕ(t) и могут быть вычислены непосредственно по графику ϕ(t).

Установим связь моментов с функцией ϕ(t). Запишем формул у прямого преобразования Лапласа для ϕ(t)

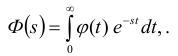
Дифференцируя, получим:

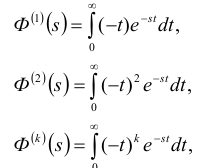
Затем получим:

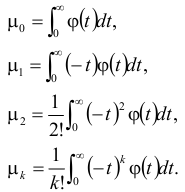
Как видно из формул моменты могу т быть вычислены по известной функции ϕ(t) . Установим связь между моментами и площадями

Преобразуем выражение для Ф(s) в следующем виде

или

Отсюда следует

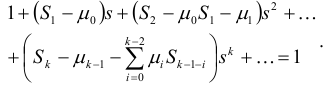
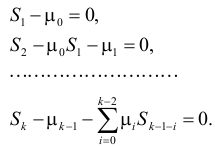
Из системы уравнений получим рекуррентные соотношения

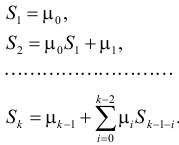
Алгоритм оценки параметров модели

1. По кривой разгона определим коэффициент усиления и запаздывание

2. Строим вспомогательную кривую

3. По кривой вычисляем моменты по соотношениям:

4. Определяем площади

5. Определяем коэффициенты и .

Статистическая идентификация линейных стационарных объектов

К данному классу относятся методы идентификации, оперирующие свойствами объектов в форме корреляционной функции, спектральной плотности и т.д.

Одной и основных форм является уравнение Винера-Хопфа.

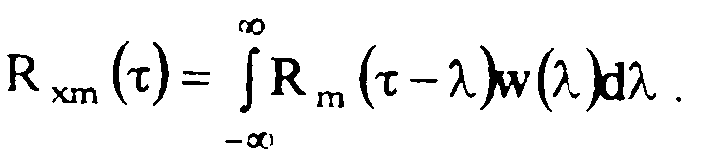
откуда определяется .

При этом можно вывести значение интервала наблюдения t в зависимости от различного вида корреляционной функции.

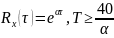
Лекция 24.09.2012

Можно показать, что ПФ W(s) равна

Пример. Пусть в ходе наблюдения получено, что

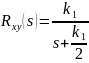
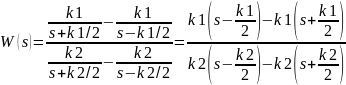
Определение ПФ по кривой разгона логарифмическим методом

В данном методе используются известные уравнения связи между входом и выходом, или уравнения свёртки

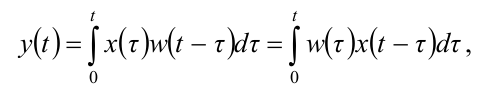
Метод заключается в аппроксимации переходной характеристики выражением типа

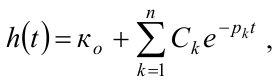(1)

где

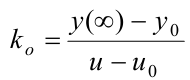
установившееся значение выходной величины объекта, соответствующее частному решению дифференциального уравнения и определяемое вынужденным движением под действием входного сигнала.

Слагаемые в сумме формулы (1) определяют свободное движение и представляют общее решение ДУ объекта, где постоянная интегрирования.

корни характеристического уравнения.

Для определенности пометим, что ПФ имеет один действительный корень, 2 комплексно-сопряженных и 2 кратных корня.

Прологарифмируем выражение

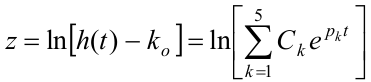
Для устойчивого объекта свободные движения с течением времени стремятся к нулю, причем время переходного процесса будет определяться корнем, имеющим минимальную действительную часть. В нашем случае, например, действительным корнем. Тогда, начиная с некоторого момента времени, слагаемыми в данном соотношении, имеющими большие действительные части, можно пренебречь и приближенно записать:

Данное уравнение является асимптотой при

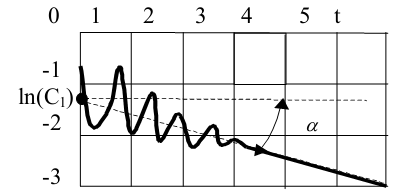
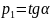
Ордината асимптоты при t = 0 равна

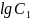
И исходя из этого

Далее можем исключить одно слагаемое, соответствующее действительному корню

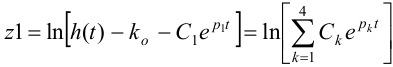
Т.е. метод заключается в том, что мы последовательно отсекаем корни и находим их графически по графику.

Начиная с некоторого момента, слагаемыми, имеющими большие действительные части, можно пренебречь и записать:

Логарифмируя, получим выражение:

Уравнение кривой, проходящей через точки, где 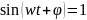имеет вид

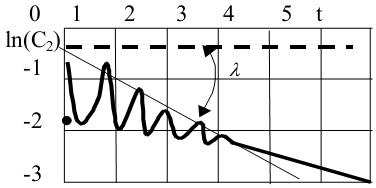
В этом случае касательную мы провели иначе. Её мы провели через точки, где синус равен 1 (этот кривой график – это sin вместе с ещё какой-то экспонентой)

Неизвестные 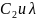находятся как и предыдущем случае, а круговую частоту w и определяем из условия

Тогда можем записать соотношение:

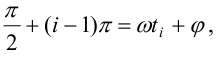
где значения времени, при которых значение переходной характеристики принимает экстремальное значение.