18 Методы начисления процентов.

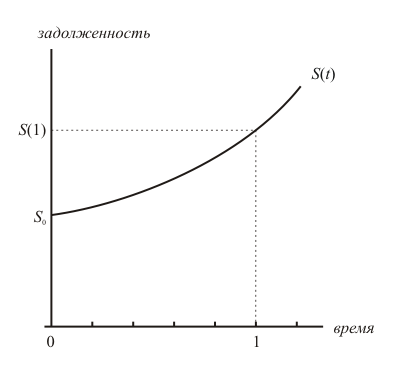
Начисляемые проценты являются платой заёмщика за пользование ссудой — никто просто так не даст пользоваться своими деньгами, точно так же, как никто не даст бесплатно автомобиль на прокат. Размер этой платы определяется с помощью так называемой процентной ставки, которая равна относительному приращению задолженности за единицу времени, то есть за год. Иными словами, если обозначить через S₀ первоначальный размер задолженности, а через S(1) — размер задолженности по истечении года, то процентная ставка определяется по формуле

i=(S(1)−S 0):  S 0      (5.1)   

Процентная ставка используется для сравнения между собой однотипных ссудных операций: чем выше процентная ставка, тем выгоднее сделка для кредитора. Это становится понятно, если переписать предыдущую формулу следующим образом:

S(1)=(1+i)S 0    (5.2)   

— отсюда видно, что S(1) тем больше, чем больше i.

существует два базовых принципа начисления процентов — метод простых процентов и метод сложных процентов.

Метод простых процентов заключается в том, что задолженность заёмщика перед кредитором возрастает с постоянной скоростью. Это значит, что график задолженности является прямой линией, проходящей через точки S₀ и S(1) = (1+ i ) S₀:

Увеличение задолженности заёмщика по методу простых процентов

Формула, с помощью которой можно найти размер задолженности в произвольный момент времени t, для метода простых процентов имеет следующий вид:

S(t)=(1+it)S 0    (5.3)   

(в этом нетрудно убедиться, если подставить в неё значения t = 0 и t = 1).

Смысл метода простых процентов заключается в том, что проценты начисляются всё время на одну и ту же сумму — начальный долг (поэтому скорость начисления процентов постоянна). В отличие от этого, метод сложных процентов характеризуется фразой «начисление процентов на проценты». Это значит, что задолженность заёмщика возрастает в геометической прогрессии: задолженность в предыдущий момент времени служит основой для начисления процентов в следующий момент:

Увеличение задолженности заёмщика по методу сложных процентов

Наглядно представить этот механизм можно следующим образом. Предположим, что вкладчик положил в банк сумму S 0   под процентную ставку i. Тогда через год на его счету будет сумма S(1)=(1+i)S 0   . Если вкладчик решит не снимать деньги со счёта, а снова их вложить с теми же условиями (реинвестировать), то уже через два года от даты совершения первого вклада на его счету будет сумма

S(2)=(1+i)S 1 =(1+i) 2 S 0  

19 Финансовая эквивалентность обязятельсв

Эквивалентные процентные ставки – такие ставки, значения, которых в конкрет­ных условиях приводят к одинаковым финансовым результа­там, т.е. замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансо­вых отношений сторон в рамках одной операции.

При необходимости замены одного де­нежного обязательства другим, например с более отдаленным сроком платежа, объединении нескольких платежей в один (кон­солидировать платежи) возникает вопрос о прин­ципе, на котором должны базироваться изменения условий контрактов. Таким общепринятым принципом является финан­совая эквивалентность обязательств.

Эквивалентными считают­ся такие платежи, которые, будучи «приведенными» к одному моменту времени, оказываются равными.

Приведе­ние осуществляется путем дисконтирования (приведение к бо­лее ранней дате) или, наоборот, наращения суммы платежа (ес­ли эта дата относится к будущему).

Если при изменении усло­вий контракта принцип финансовой эквивалентности не со­блюдается, то одна из участвующих сторон терпит ущерб, раз­мер которого можно заранее определить.

По существу, принцип эквивалентности в наиболее простом проявлении следует из формул наращения и дисконтирования, связывающих величины Р и S. Сумма Р эквивалентна S при принятой процентной ставке и методе ее начисления. Две сум­мы денег S₁ и S₂, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или нара­щенные) величины, рассчитанные по одной и той же процент­ной ставке и на один момент времени, одинаковы. Замена S₁ на S₂ в этих условиях формально не изменяет отношения сто­рон.

Сравнение платежей предполагает использование некоторой процентной ставки и, следовательно, его результат зависит от выбора ее размера.

Однако, что практически весьма важно, та­кая зависимость не столь жестка, как это может показаться на первый взгляд. Допустим, сравниваются два платежа и со сроками п₁ и п₂, причем S₁ < S₂ и n₁< п₂. Соотношение их со­временных стоимостей зависит от размера процентной ставки. С ростом i размеры современных стоимостей уменьшаются, причем при i = i₀ наблюдается равенство Р₁ = Р₂ Для любой ставки i < i₀ имеем Р₁ < Р₂. Таким образом, результат сравне­ния зависит от размера ставки, равного i₀. Назовем эту ставку критической или барьерной.

На основе равенства P1 и P2 получаем процентную ставку:

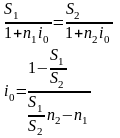
Если дисконтирование производится по сложной ставке, то критическую ставку найдем из равенства дисконтированных P1 и P2 для сложной процентной ставки.