1.4. Побудова діагностичної моделі об’єкта, заданого схемою з’єднань блоків

Побудова діагностичної моделі ґрунтується на визначенні причинно-наслідкового відношення x_i→x_j на множині {x}, що еквівалентна введенню суворого часткового впорядкування на множині змінних. Діагностична модель об’єкта являє собою замкнуту систему з l алгебраїчних рівнянь, де l невідомими є коефіцієнти причинного впливу _ij.

Імовірність P(x_i, x_j) події, що заключається у виконанні задачі спільно двома послідовно з'єднаними блоками i і j, розраховується за допомогою наступного виразу:

P(x_i, x_j) = P(x_j) = P(x_i)P(x_j/x_i).

Умовна імовірність P(x_j/x_i) визначає ступінь причинного впливу попереднього (і-го) блока на наступний (j-ий).

За припущення, що чим важливіший блок, тим менше на його працездатність повинно впливати зниження працездатності попереднього блоку, умовну імовірність P(x_j/x_i) можна представити як функцію важливості блоку, тобто:

P(x_j/x_i) = f(a_j), (1.13)

де a_j – показник, що характеризує важливість блоку, причому окремі значення функцій

(1.14)

де P₀ – задана ймовірність, що відповідає найбільшому впливу одного блоку на інший.

В якості функції f(а_j) рекомендується використати наступну:

(1.15)

Як бачимо, функція (1.15) відповідає поставленим вимогам (1.13) і (1.14).

Використовуючи вираз (1.15), можна отримати значення імовірностей виконання задачі будь-яким наступним блоком Р_j у вигляді:

(1.16)

Для побудови моделі слід побудувати граф G, вершинами якого є фактори x_i, що характеризуються імовірностями виконання P_i і невиконання q_i блоками своїх задач (число вершин рівно числу блоків).

Направлені вітки вказують напрям впливу, що визначається за схемою сполучення блоків, та оцінюється оператором _ij гілки. Індекси i та j у операторів гілки відповідають номерам факторів, що зв'язуються (перший індекс – номер фактору, до якого направлена гілка, другий індекс – номер фактору, з якого виходить гілка).

Кожній вершині x_i графа відповідають два локальні степені: М₁ – число змінних, по відношенню до яких x_i є безпосередньою причиною (число вихідних гілок), М₂ – число факторів, для яких x_i є безпосереднім наслідком (число гілок, вхідних в x_i).

1.5. Визначення функціоналів ентропії та інформації

Якщо фактор x_і включає події x_1i, ..., x_si, ..., x_ki, що визначаються імовірностями P_1i, ..., P_si, ..., P_ki, причому , то ентропія характеризує середню кількість інформації, яка несе кожна з подій x_si. Функціонал ентропії має вигляд

(1.17)

і повністю обумовлений невизначеністю фактору x_i як джерела інформації. Вибір основи логарифму визначає тільки вибір одиниці вимірювання інформації.

Перехід до бінарного причинно-наслідкового зв'язку між факторами X_i→X_j, де кожна подія x_si може бути причиною декількох наслідків, дозволяє розглянути аналогічний зв'язок між джерелом інформації і приймачем по каналу з завадами, де повідомлення x_si, що передається, у випадку правильного прийому, приймається як x_si, a при спотворенні як x_rj. Тоді кількість інформації при такій передачі

.

Середня кількість інформації, що передається по каналу з завадами

. (1.18)

Наявність декількох факторів, що є причинами для j-го наслідку, аналогічно наявності декількох паралельних каналів у одного приймача:

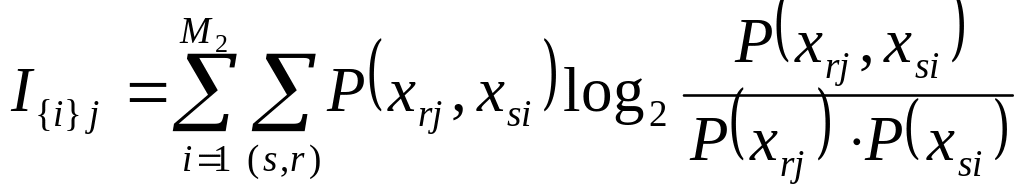. (1.19)

Коли кожний фактор визначається двома подіями, такими як виконання задачі (x_i) і невиконання задачі ( ) i-тим блоком, з відповідними ймовірностями P_i i q_i (R= r =2), то виконання задачі i-тим блоком (x_i) і виконання задачі j-тим блоком (наступним) блоком (x_j) аналогічно передачі без спотворень. Виконання задачі і-тим блоком (x_i) і невиконання j-тим ( ) рівносильне спотворенню інформації, де роль завади грає ненадійність j-го блоку. В цьому випадку вираз для ентропії у відповідності з (1.17) має наступний вигляд:

H_i = –(P_ilog₂P_i + q_ilog₂q_i).

Для одержання функціонала інформації необхідно розглянути всі поєднання подій, що входять в X_i, X_j, тобто

(x_i, x_j); (x_i, ); ( , ); ( , x_j),

і визначити їхню імовірність:

1. P(x_i, x_j) = P_j; 3. P( , ) = q_i;

2. P(x_i, ) = q_j; 4. P( , x_j) = 0,

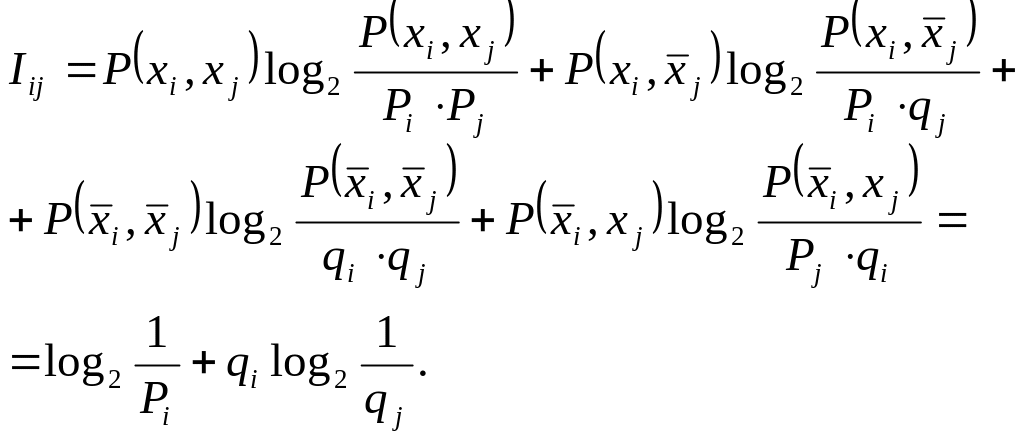(1.20)

Вираз для функціонала інформації за наявності декількох взаємодоповнюючих факторів, що є причинами для одного наслідку в відповідності до (1.19) і (1.20) набуває вигляду

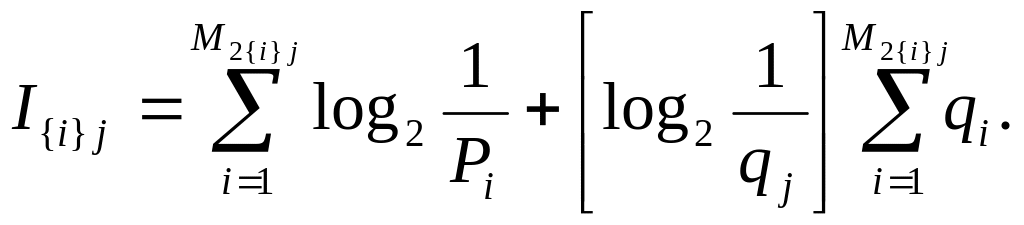
Вираз для I_{i}j відображає не лише причинні зв’язки j-го блоку і вплив невизначеності причин, але і надійність j-го блоку.

Стан складного об’єкта оцінюється вектором = (x_1, ..., x_n); i=1, 2, ..., n; x_i – відхилення і-го показника від номінального значення. Для оцінки вектора можна використати функцію f(x_1, ..., x_i, ..., x_n), що володіє наступними властивостями:

– приймає лише позитивні значення:

f(x_1, ..., x_i, ..., x_n) ≥ 0;

– якщо об'єкт в номінальному стані:

(x_1, ..., x_i, ..., x_n) = 0 → f(x_1, ..., x_n) = 0;

– чим більше f(x₁,..., x_n), тим більше відхилення стану об’єкта від номінального.

В якості f(X) для достатньо загального випадку можна використати функцію вигляду:

f(x_1, ..., x_i, ..., x_n) = ,

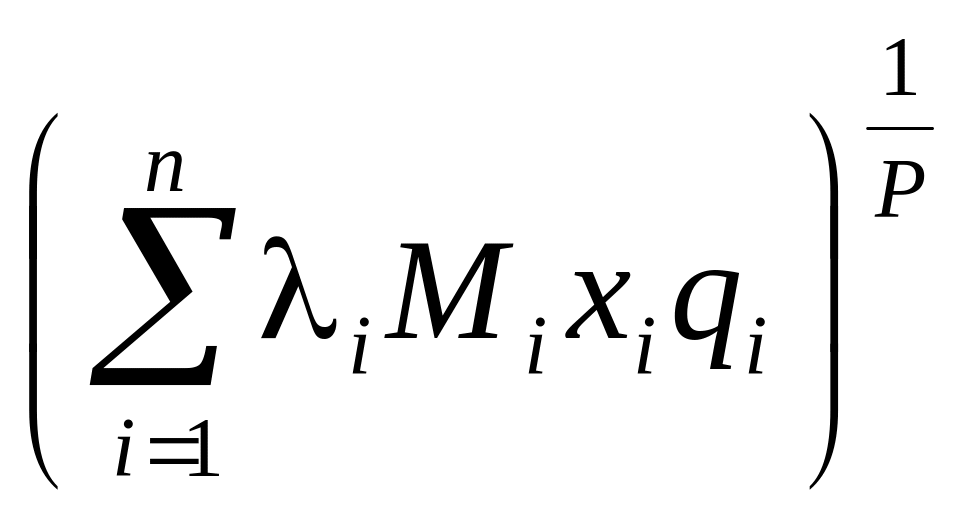де Р, q – натуральні числа; λ_i >0 – коефіцієнт, що враховує важливість показника; M_i ≥0 – коефіцієнт, що враховує вплив на і-тий показник інших показників, якщо M_i =1, то вплив відсутній.

Для функції f характерна властивість, що якщо деякий i-тий показник є найбільш важливим (має найбільший коефіцієнт λ_i), то відповідний коефіцієнт впливу повинен бути близький до одиниці (M_i ≈1).