- •Камский государственный политехнический институт
- •Методические указания для самостоятельной работы и выполнения курсовой работы для студентов экономических специальностей
- •Содержание
- •Введение
- •Общая постановка задачи динамического программирования
- •Принцип оптимальности и уравнения Беллмана
- •Общая схема применения метода дп
- •Задача распределения средств между предприятиями
- •Задача стратегического планирования
- •Задача замены оборудования
- •Указания к выполнению курсовой работы
- •Задания для самостоятельной работы
- •Задача распределения средств между предприятиями
- •Задача замены оборудования
- •Литература
Задача стратегического планирования
Предложенная схема применения методов динамического программирования также применима при решении задачи стратегического планирования предприятия.
Рассматривается задача планирования производства предприятия в течение T периодов (лет). Предприятию на планируемый период выделяют дополнительные средства. Предполагается, что технология производства в планируемом периоде не меняется. Необходимо определить план производства на каждый год, объёмы закупаемых ресурсов, оптимальный план распределения финансовых средств P по годам деятельности для получения максимального дополнительного дохода.
Введем обозначения:
![]() -
объем закупаемых ресурсов;
-
объем закупаемых ресурсов;
![]() -
складские запасы ресурсов в первый год
деятельности;
-
складские запасы ресурсов в первый год
деятельности;
- план производства продукции каждого вида;
-
нормы затрат ресурсов для производства
единицы продукции каждого вида (![]() );
);
- цены на ресурсы;
- объем выделенных ресурсов;
и - соответственно минимальный (обязательства предприятия) и максимальный объем (ёмкость рынка) производства продукции;
k – номер периода (года) деятельности предприятия.
Задача стратегического планирования состоит из 2 этапов:
Находят показатели эффективности каждого периода в зависимости от объема выделенных ресурсов Q (в результате решения задачи линейного программирования – задачи использования ресурсов).
Математическая модель:
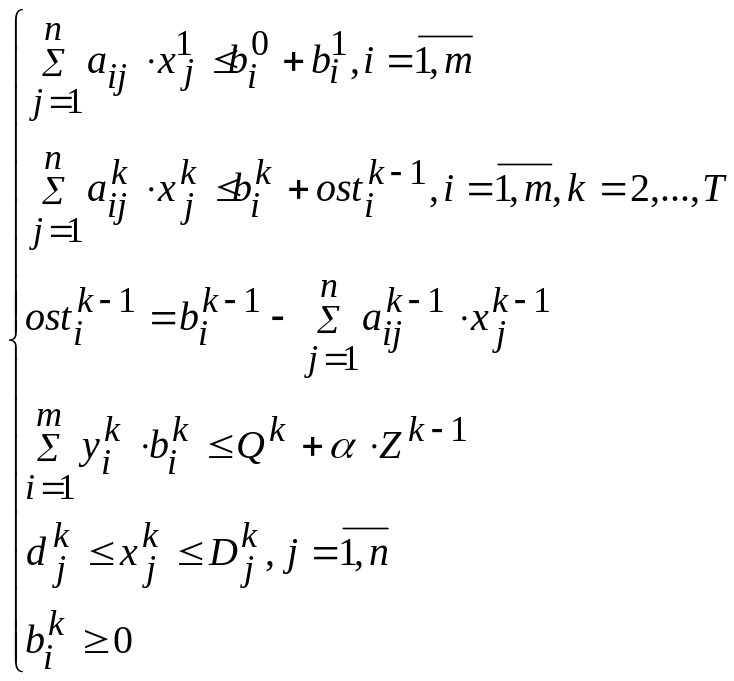
Определяют оптимальное распределение всех финансов P по периодам (годам) деятельности (методом динамического программирования).
Таким образом, можно вычислить показатели эффективности каждого периода деятельности предприятия в зависимости от выделенных финансовых средств, определить оптимальный план производства и объем закупаемых ресурсов.
Если
P
распределяется с точностью
![]() ,
то
,
то
![]() ,
можно сформировать следующую таблицу
(таблица 3):
,
можно сформировать следующую таблицу
(таблица 3):
Таблица 3
Объем выделенных ресурсов, Q |
Показатели эффективности периода деятельности в зависимости от объема выделенных средств, fi(Q) |
|||
f1(Q) |
f2(Q) |
… |
fl(Q) |
|
Q0 |
|
|
|
|
Q1 |
|
|
|
|
Q2 |
|
|
|
|
… |
|
|
|
|
Qn |
|
|
|
|
Эта таблица используется для нахождения оптимального распределения финансовых ресурсов по периодам деятельности методом динамического программирования.
Замечание:
Финансовые результаты первого года
деятельности должны повлиять на
финансовые результаты в последующие
годы. Для этого в соотношение
![]() добавляется величина
добавляется величина
![]() ,
где
,
где
![]() - норма
затрат финансовых результатов на
производство,
т.е.
- норма
затрат финансовых результатов на
производство,
т.е.
![]() .
.
Задача замены оборудования
Задача замены оборудования состоит в определении оптимальных сроков замены старого оборудования (станков, производственных зданий и т. п.) в процессе его эксплуатации. С течением времени растут производственные затраты на текущий и капитальный ремонт и обслуживание, снижаются производительность труда, ликвидная стоимость.
Поэтому в определенный момент времени возникает необходимость (экономическая целесообразность) замены старого оборудования на новое. Критерием оптимальности являются, как правило, либо прибыль от эксплуатации оборудования (задача максимизации), либо суммарные затраты на эксплуатацию в течение планируемого периода (задача минимизации).
Таким образом, задача состоит в нахождении плана-графика замены старого оборудования на новое в течение планируемого периода эксплуатации.
При построении модели задачи принято считать, что решение о замене выносится в начале каждого промежутка эксплуатации (например, в начале года) и что в принципе оборудование можно использовать неограниченно долго.
Основная характеристика оборудования - параметр состояния - его возраст t.
При
составлении динамической модели замены
процесс замены рассматривают как n
- шаговый, разбивая весь период эксплуатации
на n
шагов. Возможное управление на каждом
шаге характеризуется качественными
признаками, например,
![]() (сохранить оборудование),
(сохранить оборудование),
![]() (заменить оборудование).
(заменить оборудование).
При решении задачи замены оборудования используются следующие исходные данные:
![]() -
период планирования;
-
период планирования;
![]() -
ликвидная стоимость оборудования (
-
ликвидная стоимость оборудования (![]() );
);
![]() -
стоимость содержания оборудования (
-
стоимость содержания оборудования (![]() );
);
![]() -
первоначальная стоимость оборудования
(
-
первоначальная стоимость оборудования
(![]() ).
).
Уравнения состояний системы зависят от управления:
![]()
В
самом деле, если к k
– ому шагу
![]() ,
то при сохранении оборудования
,
то при сохранении оборудования
![]() через год возраст оборудования увеличится
на 1. Если оборудование заменяется новым
через год возраст оборудования увеличится
на 1. Если оборудование заменяется новым
![]() ,
то это означает, что к началу k
– ого шага её возраст t=0
, а после
года эксплуатации t=1,
т.е.
,
то это означает, что к началу k
– ого шага её возраст t=0
, а после
года эксплуатации t=1,
т.е.
![]() .
.
Показатель эффективности k - ого шага:
![]() .
.
Пусть
![]() - условные оптимальные
затраты на эксплуатацию оборудования,
начиная с k
- ого шага до конца, при условии, что к
началу k
- ого шага оборудование имеет возраст
t
лет.
- условные оптимальные
затраты на эксплуатацию оборудования,
начиная с k
- ого шага до конца, при условии, что к
началу k
- ого шага оборудование имеет возраст
t
лет.
Тогда уравнения Беллмана будут иметь вид:
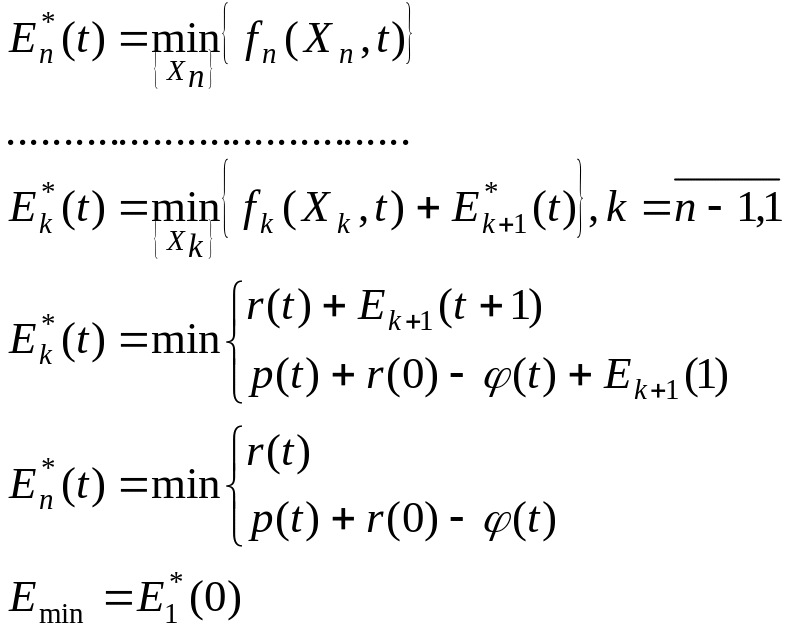
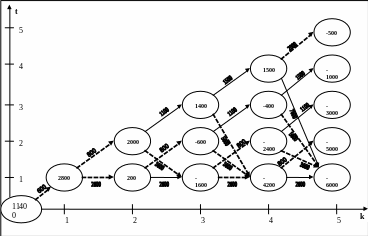
Геометрическое решение задачи замены оборудования. Схема расчетов при решении задачи замены оборудования может быть представлена в виде двухкоординатной диаграммы (графа). На оси абсцисс будем откладывать номер шага k, на оси ординат — возраст оборудования t. Точка (k-1, t) на плоскости соответствует началу k-го года эксплуатации оборудования возраста t лет. Перемещение на графике в зависимости от принятого управления на k-м шаге показано на рисунке.
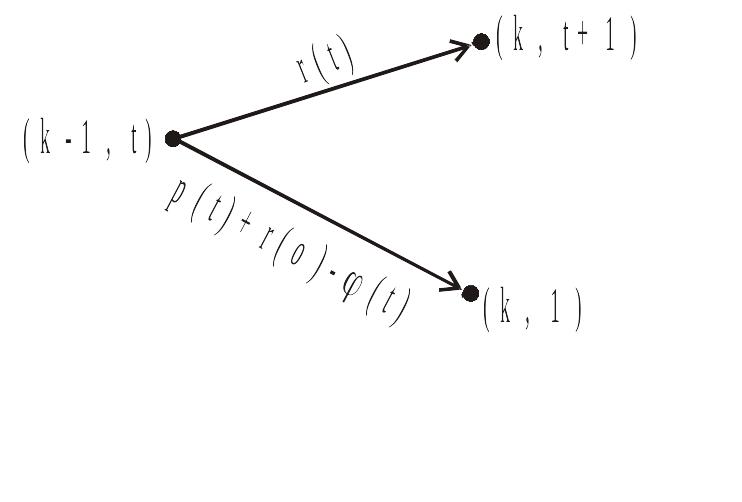
![]() затраты на сохранение оборудования, а
над отрезком, соединяющим точки (k-1;t)
и (k; 1),
запишем затраты, соответствующие замене
оборудования - управлению
.
Таким образом, будут размечены все
отрезки, соединяющие точки на графике,
соответствующие переходам из любого
состояния
в состояние
.
затраты на сохранение оборудования, а
над отрезком, соединяющим точки (k-1;t)
и (k; 1),
запишем затраты, соответствующие замене
оборудования - управлению
.
Таким образом, будут размечены все
отрезки, соединяющие точки на графике,
соответствующие переходам из любого
состояния
в состояние
.
Пример.
Оборудование
эксплуатируется в течение 5 лет, после
истечения срока продается. В начале
каждого года можно принять решение
сохранить оборудование или заменить
его новым. Стоимость нового оборудования
![]() рублей.
рублей.
Данные о затратах на содержание оборудования и ликвидной стоимости приведены в таблице 4.
Таблица 4.
-
t
0
1
2
3
4
5
φ(t)
-
6000
5000
3000
1000
500
r(t)
600
800
1100
1500
2000
-
Необходимо определить оптимальную стратегию эксплуатации оборудования, чтобы суммарные затраты с учетом начальной покупки и заключительной продажи были минимальны.
Проведем на размеченном графе условную оптимизацию.
5 шаг. В состояниях (5,t) оборудование продается, условный оптимальный доход от продажи равен ликвидной стоимости (t), но поскольку целевая функция связана с затратами, то в кружках точек (5,t) ставим величину дохода со знаком «-».
4 шаг.
Состояние (4,1).

![]()
Таким образом, если система к последнему шагу находилась в точке (4,1), то следует идти в точку (5,1) (укажем это направление пунктирной линией), т.к. затраты в этом случае будут минимальными (8000+600-6000=2600<800).
Состояние (4,2).

![]()
Состояние (4,3).

![]()
Состояние (4,4).

![]()
3 шаг.
Состояние (3,1).

![]()
В данном случае, находясь в точке (3,1), оптимально идти как в точку (4,2), так и в точку (4,1) (в обоих случаях затраты будут одинаковыми (-1600), возникает альтернативность решения).
Состояние (3,2).

![]()
Состояние (3,3).

![]()
2 шаг.
Состояние (2,1).

![]()
Состояние (2,2).

![]()
1 шаг.
Состояние (1,1).

![]()
В данном случае, находясь в точке (1,1), оптимально идти как в точку (2,1), так и в точку (2,2) (в обоих случаях затраты будут одинаковыми (2800), возникает альтернативность решения).
После
проведения условной оптимизации в точке
(0,0) получим минимальные затраты на
эксплуатацию оборудования в течение 5
лет с последующей продажей:
![]() руб.
руб.
Строим оптимальные траектории, перемещаясь из точки (0,0) по пунктирным линиям в конечное состояние .
Получаем следующие наборы точек, соответствующие управлениям:
(0,0); (1,1); (2,2); (3,1); (4,2); (5,1) -
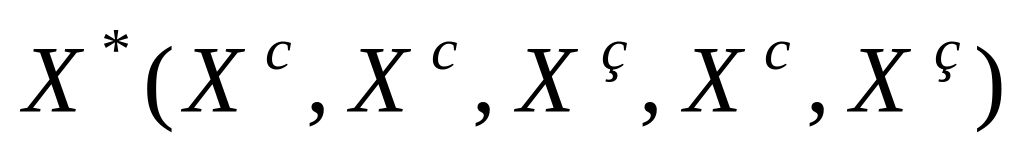 ;
;(0,0); (1,1); (2,1); (3,2); (4,1); (5,2) -
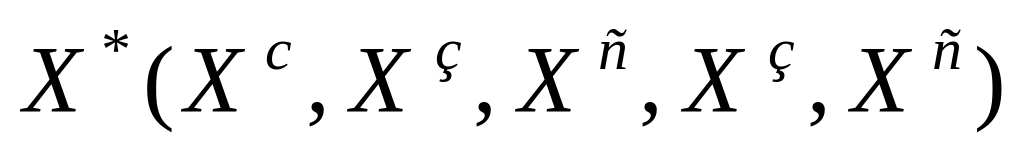
(0,0); (1,1); (2,2); (3,1); (4,1); (5,2) -
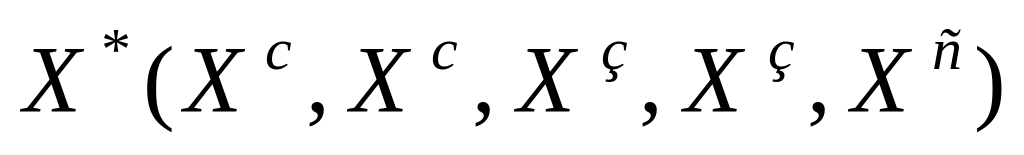 .
.
Согласно первой стратегии эксплуатации оборудования следует заменить в начале 3-его и 5-ого годов, согласно второй – в начале 2-ого и 4-ого годов, согласно третьей - в начале 3-его и 4-ого годов.
Замечания:
Стоимость приобретения оборудование зависит от года в силу изменения рыночных цен;
Затраты на содержание оборудования зависят не только от возраста оборудования, но и от года обслуживания;
Ликвидная стоимость оборудования зависит от стоимости нового оборудования в момент продажи;
Приобретаемое оборудование может иметь иные технологические характеристики, чем заменяемое оборудование, поэтому после замены оборудования изменяются экономические показатели производства (прибыль, рентабельность и др.).
В качестве критерия оптимизации в задаче замены оборудования может выступать максимизация прибыли.
В ней аналогично задаче замены оборудования с критерием минимизации затрат имеются данные о ликвидной стоимости, первоначальной стоимости и затратах на эксплуатацию оборудования в зависимости от года t.
При
этом показатель эффективности определяется
в результате решения задачи использования
ресурсов в двух вариантах - при различных
управлениях
![]() ,
,
![]() .
То есть решаются задачи планирования
производства в каждый год планируемого
периода:
.
То есть решаются задачи планирования
производства в каждый год планируемого
периода:
при сохранении оборудования (значения норм затрат ресурсов
 )
и
)
и
при замене оборудования (нормы затрат равны
 ).
При этом выполняется условие
).
При этом выполняется условие
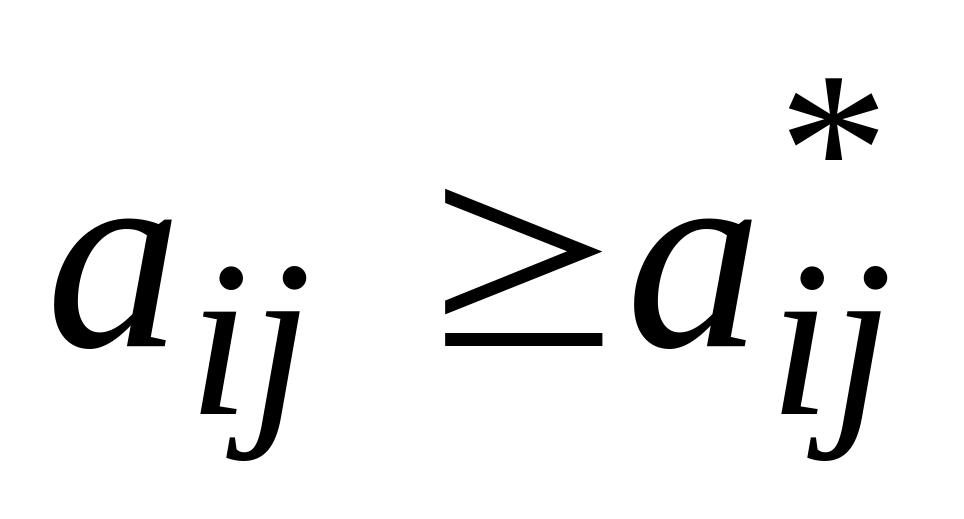 .
.
Математическая модель планирования производства в случае сохранения оборудования будет иметь следующий вид:
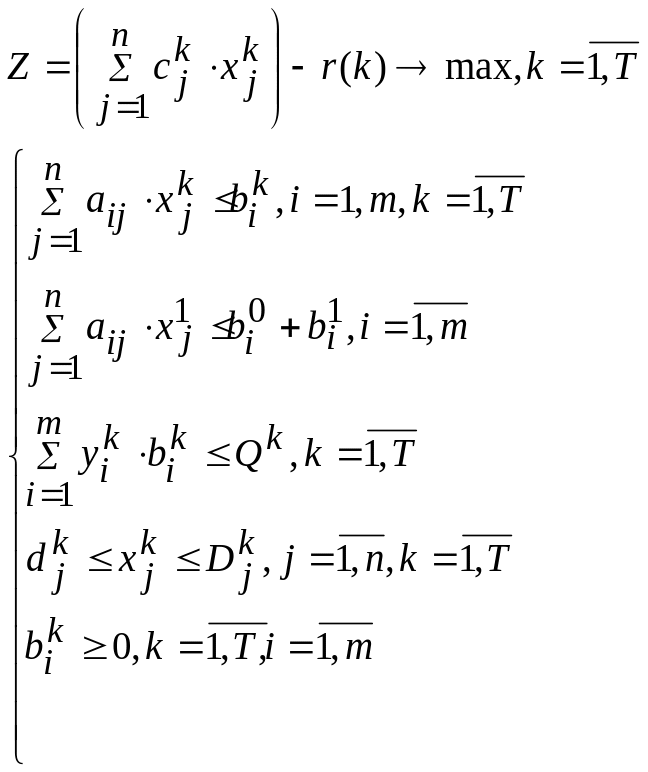
При замене оборудования модель принимает вид:
 ,
,
где p(k) – стоимость оборудования в период t;
r (k)– затраты на эксплуатацию оборудования в период t.
Вычислив показатели эффективности деятельности каждого предприятия (доход, прибыль) в зависимости от объема получаемых финансовых средств, далее используют их для нахождения оптимального плана-графика замены оборудования в течение планируемого периода методом динамического программирования.
При этом здесь, как и в задаче замены оборудования с критерием минимизации затрат, в состояниях системы, соответствующих последнему шагу, оборудование продается, и условный оптимальный доход от продажи равен ликвидной стоимости (t). Но в отличие от неё целевая функция связана уже не с затратами, а с прибылью, поэтому в кружках точек последнего шага (n,t) ставим величину дохода со знаком «+» (в задаче замены оборудования с критерием минимизации затрат на эксплуатацию необходимо ставить «-»).
В зависимости от управления графически перемещения на каждом шаге можно изобразить следующим образом:
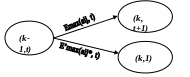
Показатель
эффективности k
- ого шага определяется как:
![]() .
.
Уравнения Беллмана (в случае обратной схемы) будут иметь вид: