Министерство образования и науки Российской Федерации

Камский государственный политехнический институт

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ и МЕТОДЫ

Динамическое программирование

Методические указания для самостоятельной работы и выполнения курсовой работы для студентов экономических специальностей

Набережные Челны

2004

Методические указания разработаны на кафедре «Математическое моделирование и информационные технологии в экономике» и предназначены для студентов экономических специальностей.

Методические указания сдержат теоретический материал, примеры решения задач распределения ресурсов между предприятиями, стратегического планирования, замены оборудования методами динамического программирования. Алгоритмы решения задач ориентированы на использование современных информационных технологий.

Приводятся темы, постановка, требования и рекомендации к выполнению курсовых работ. Для организации самостоятельной работы приводятся варианты индивидуальных заданий с примерами их решения.

Составители: Смирнов Ю.Н., Шибанова Е.В.

Набережные Челны: Изд-во КамПИ, 2004, 38 с.

Рецензент: доцент, кандидат физико-математических наук Углов А.Н.

Печатается по решению научно-методического совета Камского государственного политехнического института от 24.03.03 г.

Камский государственный

политехнический институт,

2004

Содержание

Содержание 3

Введение 4

1. Общая постановка задачи динамического программирования 5

2. Принцип оптимальности и уравнения Беллмана 7

3. Общая схема применения метода ДП 9

4. Задача распределения средств между предприятиями 10

5. Задача стратегического планирования 15

6. Задача замены оборудования 17

7. Указания к выполнению курсовой работы 29

8. Задания для самостоятельной работы 32

Литература 39

Введение

Динамическое программирование (ДП) - метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции назы­ваются многошаговыми.

К задачам, решаемым методами динамического программирования, относятся:

• стратегическое планирование предприятия на несколько лет;

• распределение дефицитных капитальных вложе­ний между возможными направлениями их использова­ния (между предприятиями, проектами и т.д.);

• разработка правил управления запасами, устанавливающими мо­мент пополнения запасов и размер пополняющего заказа;

• календарное планирования производства;

• календарное планирование текущего и капиталь­ного ремонта оборудования и его замены, основных производственных фондов и т. п.

1. Общая постановка задачи динамического программирования

Рассматривается управляемый процесс, например, экономический процесс распре­деления средств между предприятиями, использования ресурсов в течение ряда лет, замены оборудования, пополнения запасов и т. п. В результате управления система (объект управления) S пере­водится из начального состояния s₀ в состояние .

Предположим, что управление можно разбить на n шагов. Решение принимается последовательно на каждом шаге. Управление, переводящее систему S из начального состояния в конечное, представляет собой совокупность n пошаговых управлений. В качестве шага в задачах, решаемых методами динамического программирования, могут выступать временные периоды (например, годы), предприятия и др.

Обозначим через управление на k-м шаге (k=1, 2, …,n). В задаче распределения средств между предприятиями - это объем средств, выделяемых k-ому предприятию, в задаче стратегического планирования - объем средств, выделяемых на k-ом году деятельности предприятия и т.д.

Пусть - управление, переводящее систему S из состояния s₀ в состояние . Обозначим через состояние сис­темы после k-го шага управления. Получаем последовательность состояний , которую изобразим кружками (рис.1).

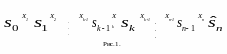
Показатель эффективности рассматриваемой управляемой опе­рации - целевая функция - зависит от начального состояния и управления: . На каждом шаге определяется объединённый (агрегированный) показатель эффективности на множестве всевозможных управлений.

Сделаем несколько предположений.

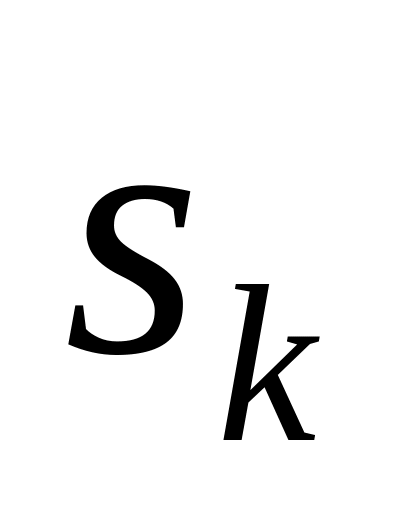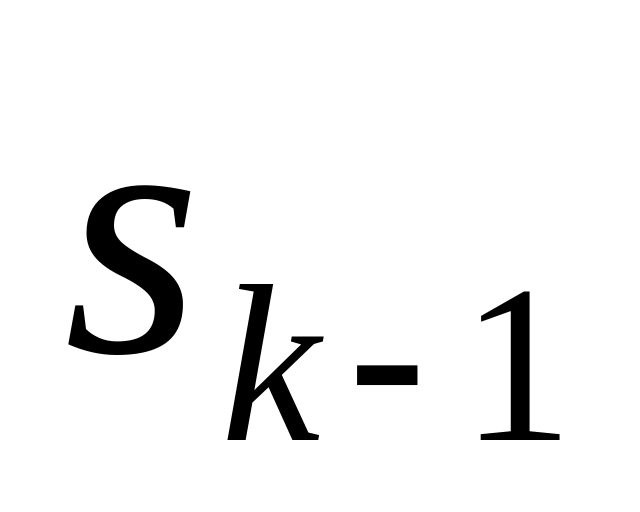1. Состояние системы в конце k-го шага зависит только от предшествующего состояния и управления на k-м шаге (и не зависит от предшествующих состояний и управлений). Это требование называется "отсутствием последействия". Сформули­рованное положение записывается в виде уравнений 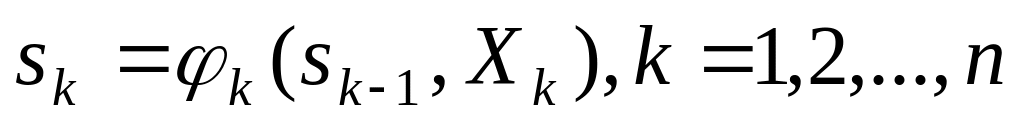, которые называются уравнениями состояний.

2. Целевая функция является аддитивной от показателя эффективности каждого шага. Обозначим показатель эффек­тивности k-го шага через 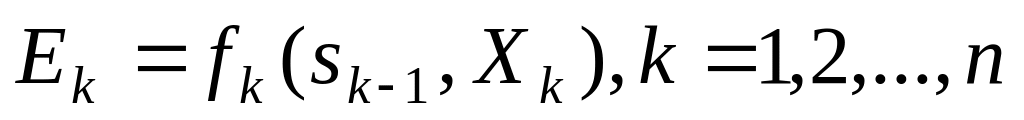, тогда .

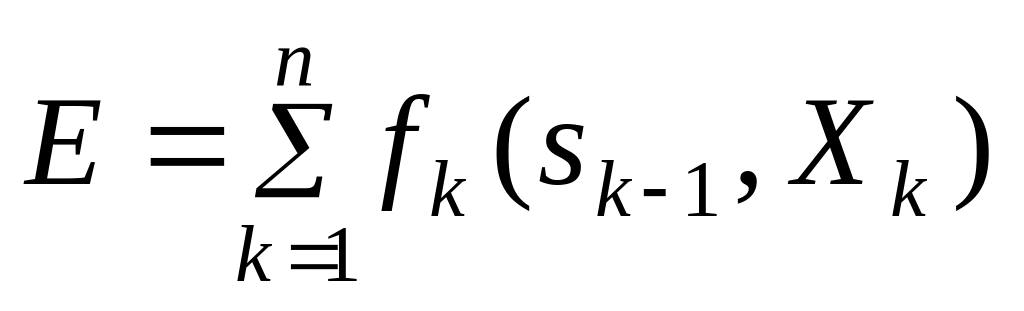Задача пошаговой оптимизации (задача ДП) формулируется так: определить такое допустимое управление X, переводящее сис­тему S из состояния s₀ в состояние , при котором целевая функция принимает наибольшее (наименьшее) значение.

Выделим особенности модели ДП:

1. Задача оптимизации интерпретируется как n -шаговый процесс управления.

2. Целевая функция равна сумме целевых функций каждого шага (целевая функция является аддитивной).

3. Выбор управления на k - м шаге зависит только от состояния системы к этому шагу, не влияет на предшествующие шаги (нет обратной связи).

4. Состояние после k - го шага управления зависит только от предшествующего состояния и управления (отсутствие по­следействия).

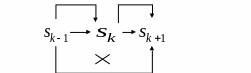
5. На каждом шаге управление зависит от конечного числа управляющих переменных, а состояние - от конечного числа па­раметров.