3.4. Показатели ремонтопригодности и долговечности.

Показатели ремонтопригодности дождевальных машин устанавливаются для оценки приспособленности к техническому обслуживанию, текущему и капитальному ремонту и отражают затраты времени, труда и стоимость выполнения этих операций.

Различают оперативное, вспомогательное и основное время ремонта и соответственно рассматриваемому времени оценивают показатели ремонтопригодности (ГОСТ 21623-76, ГОСТ 18322-78). Для ДМ в большинстве случаев оценивают среднюю оперативную трудоемкость восстановления (чел.-ч):

(3.7)

где N, К - количество соответственно исполнителей и операций ре­монта; М{t_ij} - математическое ожидание оперативного времени, затрачиваемогоi-м исполнителем на выполнение i-й операции ремонта за время наблюдений.

Приразличного рода испытаниях и наблюдениях одним из важных показателей ремонтопригодности является среднее время восстановления, характеризующее затраты времени на отыскание и устранение отказов.

Для показателей долговечности ДМ применяются: средний и гамма-процентный ресурс, средний срок службы. В качестве гамма- процентного ресурса, как правило, применяется 80-процентный ресурс (ɤ- 80 %). Это означает, что данное или большее значение ресурса будут иметь 80% машин, а 20% могут иметь меньшее значение ресурса [10].

Показатели долговечности могут устанавливаться как на машину в целом, так и на отдельные ее системы и агрегаты и относиться к тому или иному виду предельных состояний (для машины в целом - это капитальный ремонт или списание).

Оценка показателей долговечности в отличие от безотказности и ремонтопригодности осложняется тем, что большая часть данных о надежности поступает за ограниченный интервал времени, как правило, задолго до достижения предельного состояния машин. Взаимосвязь среднего R_ср и R_ɤгамма-процентного ресурса осуществляется через некоторый коэффициентК_ɤ, значение которого зависит от коэффициента вариации ν при фиксированном значении γ:

R_γ=K_γR_ср (3.8)

Коэффициент вариации ресурса , характеризующий степень его рассеяния , зависит от качества изготовления машины и условий эксплуатации.

На рисунке 3.1. приведены зависимости отношения гамма- процентных и средних показателей надежности от значенийγи коэффи­циента ν при нормальном распределении (а) и распределении Вейбулла(б).

При наблюдении в эксплуатации методы оценки показателей долговечности могут быть различными в зависимости от выборки и законов распределения ресурсов.

При неизвестном законе распределения ресурса составной части машины наиболее применимыми являются указанные ниже методы расчета ресурса.

1.Когда известна информация о наработках до предельного состояния N идентичных изделий (агрегатов, узлов, деталей), определяют средний и гамма- процентный ресурсы данного изделия. Средний ресурс:

(3.9)

где R_i- наработка до предельного состояния i-го изделия.

Рис. 3.1 (а) Зависимости отношения гамма-процентных показателей надежности от значений ɤи коэффициента ν при нормальном распределении

Для оценки гамма-процентного ресурса R_γ значения R_i располагают и нумеруют в порядке возрастания ресурса. Гамма-процентный ресурс вычисляют по интерполяции между значениями ресурсов R_kи R_k+1 порядковый номер k равен целой части выражения

L=N(100-γ)/100+0,5, (3.10)

R_γ=R_k+(K-L)(R_k+1- R_k) (3.11)

Гамма-процентный ресурс можно получить, когда объем выборки

N≥N_min=100/(100-γ) (3.12)

2. Когда известна информация о наработках до предельного состояния М изделий, а (N-М) изделий не достигли предельного состояния за время наблюдений, гамма-процентный ресурс R_γ оценивается по схеме предыдущего метода, основываясь на построении возрастающего ряда изделий, достигших предельного состояния. При этом оценку следует проводить, если число отказавших изделий М>N_min.

Можно вычислить R_γ по той же исходной информации и другим

методам, используя вероятностные сетки предполагаемых законов рас­пределения. Для этого, построив возрастающий ряд значений ресурсов , вычисляют значения i/(N+1) и соответствующие им ресурсыR_i наносят на вероятностные сетки нормального распределения и распределения Вей- булла, по нанесенным точкам строят аппроксимирующую прямую на каждой сетке и вычисляют дисперсию. Сравнивают дисперсии и по меньшей из них выбирают вид закона распределения. Гамма- процентный ресурс определяется по точке пересечения аппроксимирующей прямой с горизонтальной прямой, соответствующей F( R)= 0,2 при γ = 80%,F( R)=0,15 приγ = 85% , F(R )=0,1 приγ= 90% на вероятностной сетке выбранного вида закона распределения ресурса.

Средний ресурс в общем виде (для случая) может быть определен по вычислительной оценке R_γ по формуле

(3.13)

где К_γ - коэффициент , определяемый в зависимости от заданного значения γ, предполагаемого закона распределения ресурса и его коэффициента вариации, (рис. 3.1)

Для дождевальных машин и их составных частей нами рекомендуется использовать при коэффициенте вариации ресурса меньше 0,3 нормальный закон распределения, а при больших значениях - закон распределения Вейбулла. Коэффициент вариации ресурса оценивается по данным машин-аналогов с учетом различных факторов (вида разрушения, условий работы и уровня технологии изготовления).

Таблица 3.2.

Ориентировочные значения коэффициента вариации ресурса.

Факторы						Закон распреде­ления	Пределы изменения коэффициента вариации
Процесс разрушения		Условия работы		Уровень технологии изготовления
износ	уста­лость	ста­биль­ные	изме­няю­щиеся	высо­кий	сред­ний	Н - нормаль­ный; В - Вейбулла	от	до
+				+		Н	0,10	0,20
+					+	Н	0,20	0,30
	+	+		+		В	0,30	0,40
	+	+			+	в	0,35	0,50
	+		+	+		в	0,40	0,60
	+		+		+	в	0,60	0,70

Исключение составляет небольшое число составных частей дождевальных машин , у которых наблюдаются, как правило , только внезапные отказы (элементы автоматической системы контроля и сигнализации, элементы освещения и т.д.). Для них рекомендуется принимать экспоненциальный закон распределения ресурса.

Для ДМ и их составных частей, предельное состояние которых наступает вследствие усталостного разрушения от воздействия различных факторов, мы рекомендуем при оценке ресурса принимать закон распределения Вейбулла. Для составных частей машин, у которых преобладает влияние износа , наиболее предпочтительным является нормальный закон.

Все представленные выше оценки показателей на основе обработки статистических данных представляют собой точечные оценки. Для определения доверительных границ полученных оценок необходимо задаться доверительной вероятностьюβ (уровнем достоверности). Для ресурса определяется нижняя доверительная граница R_ср:

- для распределения Вейбулла.

R_ср=R_ср(К)^id (3.14)

- для нормального закона распределения ресурса

R_ср=R_ср-t_β,N-1

где R_ср - точечная оценка среднего ресурса; k - коэффициент, зависящий от принятой доверительной вероятности β и числа отказов m;b - параметр распределения Вейбулла, соответствующий принятому коэффициенту вариации ресурса; σ_R=R_срυ_R- оценка среднего квадратичного отклонения; t_β,n-1 - коэффициент, зависящий от принятой доверительной вероятности и числа наблюдаемых объектов (коэффициент распределения Стьюдента); N - число наблюдаемых машин.

Доверительную вероятность рекомендуется приниматьβ =0,8-0,9. Значения коэффициентовkи t_β,N-1для этих величин доверительной вероятности определяются по таблицам в зависимости от числа опытов (числа отказов). Зависимость коэффициента вариации ν_R от параметра b распределения Вейбулла показана на рис. 3.2.

Рис. 3.2. Зависимость коэффициентаν_R вариации от параметра b распределения Вейбулла

Аналогично могут быть оценены средняя наработка до отказа и среднее время восстановления. Определение нижней доверительной границы показателей надежности позволяет получить то минимальное значение, которое обеспечивается с принятым уровнем достоверности. Если ни один объект не достиг предельного состояния за время наблюдения, то оценку нижней доверительной границы среднего и гамма- процентного ресурса при допущении о распределении их по закону Вейбулла (как самому универсальному для ДМ и их составных частей) ре­комендуется проводить на основании номограмм, (рис. 3.3)

По принятому значениюγи установленным коэффициентам вариацииγ_R и параметра b распределения Вейбулла оценивают коэффициент ε. Нижняя доверительная граница R_γ при доверительной вероятностиβ=0,8 определяется как

(3.16)

где Т_cр- средняя наработка на отказ.

Нижняя доверительная граница среднего ресурса может быть оценена по нижней доверительной границе Rγ

R_ср=R_γK_γ, (3.17)

гдеК_γ - коэффициент, определяемый в зависимости отν_R . (рис.3.2) Номограмма для определения нижней доверительной границы гамма-процентного ресурса (на рис. 3.3) дана для γ=80%. [23]

Для примера приведем некоторые полученные численные данные по ремонтопригодности ДДА-ЮОМА. Наработка на отказ ДДА-ЮОМА в доремонтном периоде составляет 150-230 часов. После проведения ремонта она снижается на 40-45%, а затраты на устранение последствий отказов возрастают примерно в 2 раза. [17]

На насос-редуктор приходится 23-28% всех отказов и 40-60% общих затрат на устранение их последствий и это несмотря на то, что ежегодно 50-70% насос-редукторов ремонтируются на специальных предприятиях и в хозяйствах.

Исследованием установлено, что в связи с неравной прочностью насоса и редуктора целесообразно, наряду с полнокомплексным ремонтом насоса-редуктора, производить ремонт отдельных деталей и узлов.

Выявлена необходимость повышения долговечности рабочего колеса и защитных колец насоса.

Исследования долговечности дождевальных машин показывают, что часть узлов и деталей имеет разный ресурс, например, у "Фрегата", в зависимости от конструктивной длины машины, т.к. тележки проделывают неодинаковый путь за одно и то же время и износ узлов различен. Деталей, подверженных механическому износу, в машине относительно немного: около 3880 шт. или приблизительно 40% общего числа, не считая крепежных изделий (230 наименований). Из них 2084 шт. (130 наименований) имеют ресурс менее 20 тыс.ч., то есть большая часть машины (приблизительно 80% по числу деталей) имеет ресурс более 20 сезонов при интенсивном использовании (средняя ежегодная нагрузка 1000 ч). В свою очередь, среди выше названного числа наименований (130) имеется лишь 20 наименований относительно быстроизнашиваемых деталей (1216 шт.) с переменным по длине машины ресурсом.

На основании исследований износов деталей можно определить скорости изнашивания и ресурс основных быстроизнашивающихся деталей.

Скорость изнашивания V определяем по зависимости - отношение величины износа детали 8 к наработке машины X к моменту проведения замеров

V = δ/t.(3.18)

Износ втулок, пальцев и других деталей, как правило, неравномерный, поэтому в расчетах принимаются значения средних максимальных односторонних износов. Выравнивание значений замеров износов производится по способу наименьшей средней ошибки в предположении, что скорость изнашивания изменяется по длине машины по закону, близкому к прямой линии вида у=Ьх. Отклонения фактических значений от средней колеблется в пределах 1,5-40%.

Ресурс τ детали определяется по формуле:

t=[δ]/V(3.19)

где[δ]- допустимая величина износа.

Допустимая величина износа отдельных деталей берется с учетом технических требований или исходя из расчета потери прочности детали в результате ее износа.

По данным зависимостям (3.18, 3.19) можно определить либо число ежегодно заменяемых деталей (в соответствии с конкретной годовой выработкой машины), либо общее число деталей, которое необходимо заменить до выработки нормативного срока службы машины.

При проведении исследований сотрудниками ВНПО "Радуга" по определению рациональной номенклатуры ЗИП для капитального ремонта все узлы и детали "Фрегат" были сгруппированы по наиболее характерным признакам потери работоспособности, (табл. 3.3) [31]

Как видно из таблицы, узлы и детали имеют ресурсы, зависящие от различных причин и условий. Так, узлов и деталей, подверженных различного вида износам (механическому, гидроабразивному) насчитывается 1298 шт. 72 наименований. Имеется относительно много узлов и деталей, подверженных воздействию коррозии - 1492 шт. 71 наименования. Значительную часть составляют узлы и детали, ресурс которых в основном зависит от воздействия различных климатических условий эксплуатации машин - 524 шт. 56 наименований.

Таблица 3.3.

Группирование узлов и деталей дождевальной машины «Фрегат» по наиболее характерным признакам потери работоспособности.

	Количество	Число узлов и	Ориентиро­
Наименование группы	Наименований	деталей, шт	вочная масса,
	узлов и дета­		кг
	лей, шт
1. Узлы и детали с ресурсом,	56	524	5020
не зависящим от наработки и
длины машины (стойка не­
подвижной опоры, попере­
чина, проволока и т.д.)
2. Узлы и детали с ресурсом,	26	227	4300
зависящим от наработки
машины (колено поворот­
ное, трубы, дождевальные
аппараты)
3. Узлы и детали с ресурсом,	46	1071	2900
переменным по длине и зави­
сящим от наработки (колеса,
детали гидропривода, стопо­
ры и т.д.)
4. Резино-технические и	23	473	170
пластмассовые узлы и дета­
ли, подверженные старению
(напорные шланги, манжеты,
сливные трубы и т.д.)
5. Узлы и детали, подвер­	71	1492	1030
женныезначительному воз­
действию коррозии
(переходники, тросы, муфты)
6. Крепежные изделия	62	7335	170
(болты, винты, гайки,
шайбы)

Исходя из вышеизложенного, в номенклатуру ЗИП для капитального ремонта нами включены узлы и детали, ресурс которых не превышает полного ресурса машины до списания при продленном сроке службы (около 18 тыс. ч); подверженные старению и коррозии; имеющие в практике эксплуатации случайные или аварийные поломки и деформации, а также выходящие из строя во время разборочно-сборочных работ и устанавливаемые при модернизации машины.

На основании ресурсных испытаний и исследований [31] были определены ресурсы узлов и деталей дождевальной машины "Фрегат" (различных шайб, узлов и деталей с ресурсом до 10 и от 10 до 20 тыс. ч), характеристики рассеивания которых достаточно удовлетворительно описываются законом нормального распределения, характеристики рассеивания остальных узлов и деталей описываются законом распределе­ния Вейбулла. (рис. 3.4)

Кроме того, довольно много узлов и деталей по длине машины имеют переменный ресурс, (рис. 3.5) Практически все узлы и детали последней тележки имеют ресурс до 10 тыс. ч. Увеличение ресурса происходит по мере приближения к неподвижной опоре. На первой тележке ресурс большинства узлов и деталей превышает 20 тыс. ч.

Таблица 3.4.

Группирование узлов и деталей "Фрегата" по ресурсу

Наименование группы	Ресурс	Количество	Число	Ориенти­
	(в границах с довери­тельной вероят­ностью а =0,8),	наименован	узлов и	ровочная
		ий узлов и	деталей,	масса,кг
	ТЫС. ч.	деталей	шт.
1. Узлы и детали с ре­	4,49<8,75<13,0	39	704	241
сурсом до 10 тыс. ч
2. Узлы и детали с ре­	11,23<14,83<	27	476	300
сурсом от 10 до 20	18,43
тыс. ч
3. Узлы и детали с ре­	23,68<101,92<	110	1536	9980
сурсом свыше 20тыс.ч	199,62
4. Крепежные изделия	5,02<14,35<	31	4802	150
(болты, винты, гайки)	25,09
5. Шайбы	32,74<69,16< 105,57	17	2112	10
6. Другие стандартные	2,91<13,87<	15	412	10
изделия	24,69
7. Узлы и детали с пе­	мин.	46	1071	2900
ременным по длине	3,5<6,65<9,83
машины ресурсом	средний
	4,67<12,52< 21,49 макс. 1,45<64,8< 136,78

Значительная часть узлов и деталей имеет ресурс 20 лет. Тем не менее часть таких узлов и деталей, имеющая повреждения после аварийных поломок машины и по другим причинам, также требует замены при капитальном ремонте. Так, например, при аварийных поломках за 10 лет эксплуатации имеют повреждения: трубы - около 14%, тросы - 10%, рамы тележек - 10%, тросовые опоры - 15 % и др. У машин, работающих на двух позициях, при транспортировке с одной позиции на другую повреждается около 40 % деталей неподвижной опоры (полозья, цепи, стойки).

Анализ статистических данных показывает, что средняя наработка на отказ на 6-й год эксплуатации снижается до 50 ч против 74 ч у машин третьего года эксплуатации, или на 48%. Установлено, что доля износовых отказов на 7-й год эксплуатации увеличивается до 60% общего числа отказов. Кроме того, с увеличением срока эксплуатации ДМ "Фрегат" возрастает число аварийных поломок машины. Трудоемкость устранения таких поломок колеблется от5 до 52 чел.-ч и в среднем составляет 15 чел.-ч.

Для повышения срока службы дождевальных машин необходимо своевременное и качественное проведение технических обслуживаний в соответствии с требованиями руководства по эксплуатации и рекомендаций по техническому обслуживанию и хранению.

Нами построен график наработки машин ДДА-100МА с указанием группы сложности отказов, (рис. 3.6) Из этого графика видно, что большее число отказов приходится на период до проведения ТО-2 и на период после проведения ТО-3, также видно, что это отказы 1 и 2-й группы сложности. Из чего можно сделать вывод о недостаточно высоком уровне технического обслуживания ДМ.

3.5. Расчет эксплуатационной надежности дождевальных машин ДДА-100МА, "Волжанка" и "Фрегат".

На практике для определения вероятности безотказной работы P(t) или вероятности отказа Q(t) по результатам статистических данных об отказах элементов ДМ при их эксплуатации используют обычно метод непосредственного подсчета вероятностей.

(3.20)

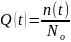(3.21)

где N₀ - количество однотипных видов элементов, за которыми велось наблюдение в течение времени t; n(t) - число отказавших образцов за время t.

С использованием алгоритма, предложенного Ильиным Ю.А. [47,48], в соответствии с полученными значениями была определена функция распределения наработки элементов дождевальных машин до отказа:

(3.22)

Алгоритм позволил также вычислить статистические значения интенсивностей отказов λ_i(t) по формуле

(3.23)

Вероятность безотказной работы, а также среднее время наработки на отказ определены в виде

P_i=1-F_i(t) (3.24)

(3.25)

где t_i-i-ое значение случайной величины наработки элемента ДМ на отказ.

При расчете вероятности безотказной работы дождевальных машин мы использовали построенное "дерево отказов и классификацию отказов элементов ДМ и рассматривали отказы, приводящие к полному прекращению работы машин. Предполагая, что в условиях установившейся эксплуатации поток отказов подчиняется нормальному закону распределения были получены следующие результаты.

Для ДДА-100МА вероятность безотказной работы была рассчитана по формуле:

Р_дда^—Р_{всас.линии}Р_{гидросистемы} Р _насосаР_фермы(3.26)

ГдеР_{всас.линии}Р_{гидросистемы} Р _насосаР_фермы- соответственно вероятность безотказной работы элементов всасывающей линии, гидросистемы, насоса и фермы.

Для рассматриваемой выборки из 22 машин вероятность отказа всасывающей линии 0,35. При этом наблюдалось 4 критических отказа этой подсистемы, соответственно вероятность безотказной работы составилаГ_{всас.линии}⁼ 0,92. Вероятность безотказной работы гидросистемы Р_{гидросистемы}=0,85 при вероятности отказа 0,18 и двух отказах, приведших к прекращению подачи воды. Вероятность безотказной работы насоса и фермы соответственно

Р_насоса =0,87 и Р_фермы—0,97 , так как вероятности их отказов 0,2 и 0,18, а имели место 2 отказа насоса и 1 отказ фермы. Веро­ятность безотказной работы дождевальной машины ДДА-100МА составилаР_дда= 0,92-0,85-0,87-0,97=0,66.

Аналогичным образом были рассчитаны показатели безотказной подачи воды дождевальными машинами "Волжанка" и "Фрегат" при выборке наблюдений 20 и 25 машин по формулам:

Р_{«Волжанка»}=Р_{прис.устр}. Р_{прив.тележка}Р _{трубопровод} =0,9-0,93-0,86=0,72 (3.27)

Р_{"Фрегат"}=Р_{прис.устр}.Р_{гидропривод}Р_{системаавтом}.Р_{трубопр}=0,96-0,7?0,87-0,98=0,63(3.28)

Полученные результаты подтверждают необходимость повышения уровня эксплуатационной надежности ДМ, так как реальные значения показателей ниже установленных нормативами значений (0,9) из-за дефектов узлов и деталей по вине завода-изготовителя, неудовлетворительного технического обслуживания и неправильной организации работы операторов-дождевальщиков, некачественной наладки и регулировки систем обеспечения безостановочной работы ДМ, исчерпания ресурса работы элементов ДМ, из-за истекшего срока эксплуатации, не соблюдения требований, предъявляемых к качеству воды, поступающей в дождевальную машину.