Кинематическая схема привода представлена на рисунке 1.1.

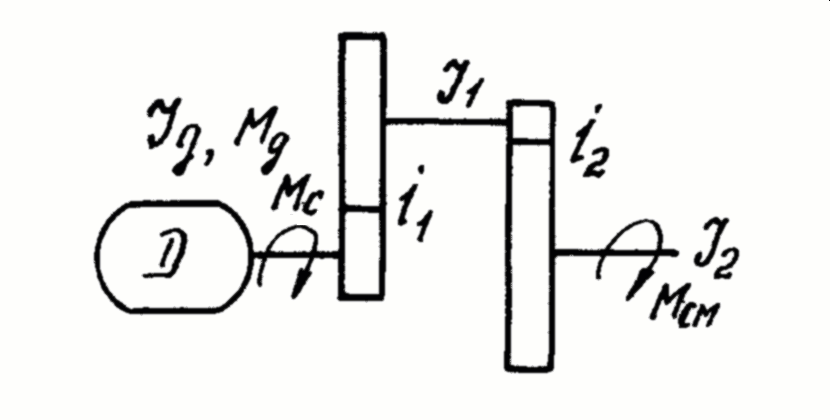
Рисунок 1.1- Кинематическая схема привода

Момент инерции рабочего вала определяется по формуле:

(1.1)

где, - момент инерции,

N-номер варианта, 70.

1.2 Расчёт основных параметров

Предварительно рассчитаем ряд величин.

Мощность, потребляемая двигателем из сети при работе в номиналь­ном режиме определяем по формуле:

(1.2)

Номинальный ток двигателя:

(1.3)

Ток возбуждения в номинальном режиме:

(1.4)

где, - напряжение на обмотке возбуждения; для параллельного возбуждения,

Номинальный ток якоря для параллельного возбуждения:

(1.5)

.

Сопротивление цепи якоря, включающее сопротивления дополнительных полюсов и компенсационной обмотки, находим из условия, что поте­ри мощности в цепи обмотки якоря составляют половину общих потерь в двига­теле:

(1.6)

Частота вращения при идеальном холостом ходе определяем по формуле:

(1.7)

Номинальный момент на валу двигателя:

(1.8)

.

Номинальное сопротивление цепи якоря:

(1.9)

1.3 Приведение моментов к валу двигателя

Кинематическая схема, приведенная на рисунке 1.1, содержит две зубчатые пе­редачи, трансформирующие движение вала двигателя к валу 2 рабочей машины. В результате изменяется частота вращения и, следовательно, величина момента. Привести статический момент сопротивления рабочей машины к валу двигателя можно по равенству мощностей на валах двигателя и рабочей машины с учётом потерь в передачах. Тогда имеем:

(1.10)

где, - передаточные числа, 24 и 4 соответственно;

- КПД зубчатых передач,0.94 и 0.96 соответственно.

Приведённый момент инерции можно найти, соблюдая закон сохранения энергии, по выражению:

(1.11)

1.4 Расчёт резисторов пускового реостата

Одним из способов ограничения пусковых токов двигателей постоянного тока (ДПТ) является включение в цепь якоря на момент пуска дополнительных резисторов. Необходимая величина их сопротивлений может быть найдена из ус­ловий ограничения пускового тока и создания необходимого пускового момента.

Минимальная величина пускового тока ДПТ обычно колеблется в пределах:

(1.12)

Пиковый максимальный ток определяется по формуле:

(1.13)

В относительных единицах получаем :

1.4.1 Аналитический метод расчёта сопротивления пусковых резисторов

Возьмём за основу отношение:

(1.14)

.

Сопротивление первой ступени (смотрите рисунок 1.2) определяем по формуле:

(1.15)

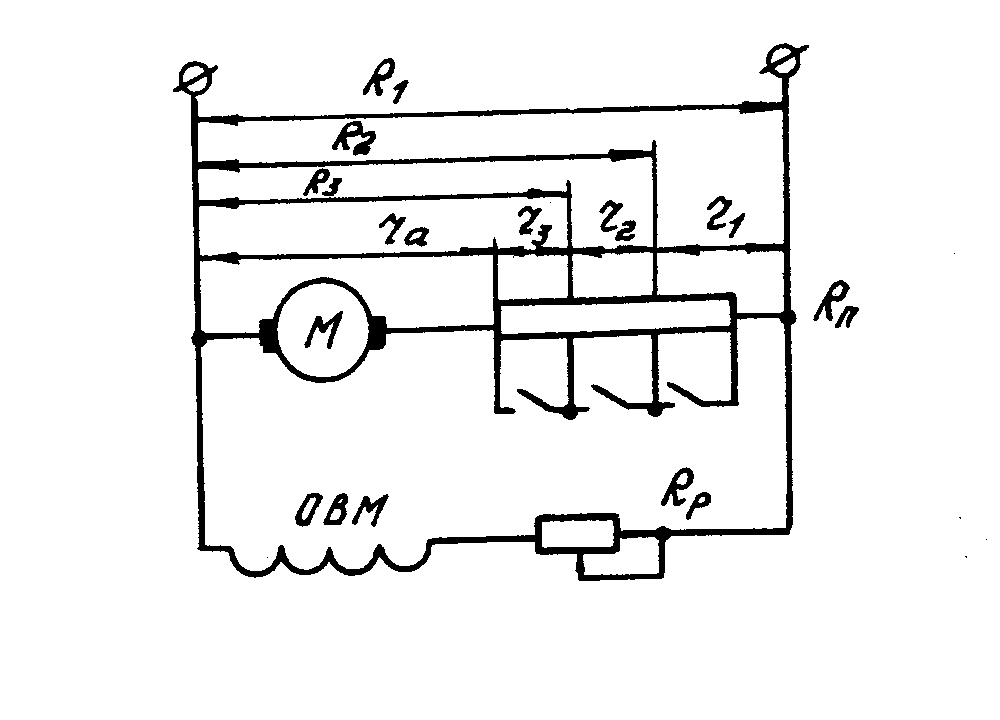
Рисунок 1.2- Схема включения резисторов

Для всех последующих ступеней (до j = z), сопротивление резисторов определяем по формуле:

(1.16)

Сопротивление секций (смотрите рисунок 2) находим по формуле:

(1.17)

получаем,

Полное сопротивление пускового реостата:

(1.18)

2. Графический метод расчёта пусковых резисторов

Построив пусковую диаграмму (смотрите рисунок 1.3) определяем сопротивления секций пускового реостата.

Для этого измеряем отрезки ab, be, cd, de; равные соответственно , , , мм.

Сопротивления секций определяются отношениями:

(1.19)

(1.20)

Сопротивления ступеней пускового реостата определяются по формулам:

(1.21)

(1.22)

(1.23)

Сопоставив сопротивления, рассчитанные обоими способами, убеждаемся в правильности их расчёта, погрешность составляет меньше пяти процентов.

1.5 Расчёт переходных процессов при пуске ДПТ

Изменение тока двигателя в процессе пуска описывается уравнением:

(1.24)

где, - ток, обусловленный моментом сопротивления (нагрузкой) на валу двигателя;

- начальное значение тока, в данном случае

- электромеханическая постоянная времени:

(1.25)

где, - добавочное сопротивление в цепи якоря (часть ступеней или полное сопротивление пускового реостата);

J- приведённый момент инерции.

На основании (1,24) при постоянном моменте сопротивления и начальном токе, равном , можно записать:

(1.26)

где, t_x – текущее время разгона на той или иной ступени пускового реостата;

- электромеханическая постоянная на той же ступени, определяемая суммарным сопротивлением цепи якоря ( на данной ступени.

Ток нагрузки пропорционален моменту сопротивления, приведённому к валу двигателя и определяется по формуле:

(1.27)

.

Время разбега на каждой ступени пускового реостата определяется по формуле:

(1.28)

Определим электромеханические постоянные на каждой ступени пускового реостата по (1.25):

Аналогично, получаем:

и на естественной характеристике,

Найдём время разгона на каждой ступени:

Аналогично, получаем:

.

В пределах каждого t, каждой ступени определяем ток по (1.26):

По данным расчёта (смотрите таблицу 1) строим кривые изменения тока ( смотрите рисунок 1.4).

Кривые изменения частоты вращения строим аналогично кривым тока для тех же значений времени и соответствующих электромеханических постоянных времени по уравнению:

(1.29)

где, - частота вращения в конце предыдущей ступени, для первой ступени

= 0;

- установившаяся частота вращения при заданном моменте сопротивления и конкретном сопротивлении цепи якоря каждой ступени пускового реостата:

(1.30)

Аналогично, для других ступени пускового реостата получаем:

Расчет частоты вращения производим для тех же моментов времени, что и расчёт пусковых токов:

.

По данным расчёта (смотрите таблицу 1) строим кривые изменения частоты вращения (смотрите рисунок 1.4).

Таблица 1- Данные расчета разгона двигателя

Характеристики	Время разбега по ступеням t, c		Ток двигателя в процессе пуска I, А	Частота вращения в процессе пуска n, об/мин
Первая ступень	t1=0	-	1028	0
	1/3t1	1,445	810,16	241,655
	2/3t1	2,87	660,101	408,405
	t1	4,334	556,554	523,47
Вторая ступень	t2=0	4,334	1028	523,47
	1/3t2	0,78	810,16	654,348
	2/3t2	1,56	660,101	744,659
	t2	2,347	556,554	806,977
Третья ступень	t3=0	2,347	1028	806,977
	1/3t3	0,42	810,16	877,859
	2/3t3	0,85	660,101	926,771
	t3	1,27	556,554	960,552
Естественная характеристика	tм=0	1,27	1028	960,552
	1/3tм	0,82	584,138	1039
	2/3tм	1,65	420,988	1068
	tм	2,474	360,968	1078

1.6 Расчет резисторов реостата возбуждения

Двигатели постоянного тока имеют достаточно широкий диапазон регули­рования частоты вращения, что выгодно отличает ДПТ от всех других типов двигателей. Одним из способов регулирования является ослабление магнитного потока возбуждения путем введения в цепь возбуждения специального регулиро­вочного реостата.

Частота вращения при переходе с одной ступени реостата на другую изменяется по линейному закону.

Расчет ведется для номинального тока якоря:

(1.31)

где, k-порядковый номер ступени регулирования от 0 до m;

- приращение частоты вращения,

(1.32)

Тогда,

.

Аналогично, получаем:

=1272 об/мин,

Таким образом, для получения любой иной, отличающейся от номинальной, частоты вращения поток возбуждения должен быть уменьшен до величины:

, (1.33)

По найденному потоку определяем необходимый ток возбуждения по универсальной кривой намагничивания двигателей постоянного тока 1, рис. 1.5.

Переход к абсолютным величинам осуществляем следующим образом:

(1.34)

Аналогично, для других значений потока (смотрите таблицу 2.)

Таблица 2- Значения потоков и токов возбуждения

,о.е.	1	0,833	0,694	0,578	0,482
,о.е.	1	0,6	0,5	0,31	0,25
,А	11.579	6,947	5,789	3,589	2,895

Сопротивление цепи возбуждения k-ой ступени реостата возбуждения определяется по формуле:

(1.35)

Аналогично, для других ступеней получаем:

Сопротивление соответствующей секции реостата определяется по формуле:

(1.36)

где, при к = 0,

Так для к=1 получаем:

Аналогично для других секций:

1.7 Расчет режима динамического торможения

При динамическом торможении якорь двигателя отключается от питающей сети и включается на некоторый тормозной резистор. Двигатель переходит в генераторный режим с изменением направления тока в цепи якоря. Задавшись необходимым током торможения, можно определить величину тормозного резистора.

Ток торможения принимаем:

(1.37)

где Ц – последняя цифра номера варианта, 0.

В еличина тормозного резистора определяется по формуле:

(1.38) где, - частота вращения в начальный момент торможения, 1078 об/мин.

Электромеханическую постоянную времени при торможении находим по формуле:

, (1.39)

где, - электромеханическая постоянная на естественной характеристике, 0,619.

Время торможения до полной остановки определяем по формуле:

(1.40)

Тормозные характеристики представлены на рисунке 1.5.

2 Асинхронные двигатели в системах электропривода

Необходимо: по заданной нагрузочной диаграмме электропривода определить эквива­лентную мощность и выбрать асинхронный двигатель с фаз­ным ротором. Произвести про­верку выбранного двигателя на нагрев по методу средних потерь, а также проверку на пере­грузочную способность при снижении напряжения в сети. Произвести расчет теплового режима выбранного двигателя при заданной нагрузочной диаграмме.

Определить сопротивление добавочного резистора, который необходимо включить в цепь ротора выбранного двигателя для снижения частоты вращения на заданную величину при номинальном моменте сопротивления. Построить ес­тественную и реостатную механи­ческие характеристики выбранного двигателя. Рассчитать сопротивления секций пускового резистора и потери электрической энергии при реостатном и прямом пуске.

1. Исходные данные

Номер варианта, N…………………………………………………………………70;

Мощность на ступенях нагрузки:

Синхронная частота вращения,

Снижение частоты вращения ротора от номинальной,

Длительность ступеней нагрузки, мин:

Снижение напряжения в питающей сети для проверки выбранного АД на перегрузочную способность выбираем 10% от номинального;

Число ступеней пускового реостата: z=2.

2.2 Расчёт мощности и выбор АД

Многоступенчатый график нагрузки, характеризующий длительный пере­менный режим работы электропривода (смотрите рисунок 2.1 ), приводим к равномерно­му, воспользовав­шись понятием эквивалентной (среднеквадратичной) мощности, определяемой по формуле:

, (2.1)

где, n – число ступеней нагрузки;

- соответственно мощность и продолжительность нагрузки каждой ступени гра­фика, включая паузу.