
- •«Оптимальное планирование работы флота судоходной компании»
- •«Исследование операций в транспортных системах»
- •Введение
- •Характеристика флота и направлений перевозок
- •1.1. Описание портов Порт Херсон
- •Порт Осло
- •Порт Веракрус
- •Подготовка исходных данных и составление математической модели задачи
- •3. Нахождение оптимального плана для работы флота и оптимальных схем движения судов
- •4.Расчет основных плановых показателей работы флота
- •Список литературы
Подготовка исходных данных и составление математической модели задачи
2.1. Построение возможных вариантов схем движения судов
Названные суда применяются для перевозок на 6 выбранных участках:
Херсон – Осло (гружённый, Ql= 380 тыс. т.)
Херсон – Веракрус (гружённый, Ql= 300 тыс. т.)
Вераксур – Херсон (гружённый, Ql= 210тыс. т.)
Осло – Веракрус (гружённый, Ql= 180тыс. т.)
Осло – Херсон (балластный) груженый
Херсон – Веракрус (балластный)
На основе заданных участков работы флота строим всевозможные варианты схем движения судов.
Правила составления схем:
- схемы должны быть замкнуты
- в схеме не должны встречаться подряд два или более балластных участков
- каждый порт входит в схему 1 раз, за исключением начального порта, который входит в схему дважды – как начальный и как конечный.
Исходя из данных правил, мы имеем такие схемы движения:
Херсон
 Осло
Осло
 Веракрус
Веракрус
 Херсон
ХерсонХерсон Осло

 Херсон
ХерсонХерсон
 Веракрус
Херсон
Веракрус
ХерсонВеракрус Херсон
 Веракрус
Веракрус
Варианты схем движения судов представляются в графическом виде. Груженые участки в схеме движения обозначаются сплошной линией, а балластные – пунктирной.
2.2.Расчет нормативов работы судов на схемах движения
Для полученных схем движения рассчитываются следующие нормативы:
а) время рейса судна i – го типа на j – ой схеме движения в сутках.
tij
= ∑ til
(i = ;
j =
;
j = ),
(1)
),
(1)
где til – норматив времени работы судна i – го типа на l - ом участке, сут., который включает валовое стояночное время в порту погрузки, валовое время перехода на участке и валовое стояночное время в порту выгрузки;
суммирование выполняется по участкам, входящим в схему (l є j);
t11 - время рейса 1-го типа судна на 1-ой схеме:
t11 = tx11 + tcm11 + tx14 + tcm14+ tx13 + tcm13
t11 =25+26+20+47+22+45=185 (суток).
Результаты расчета для остальных типов судов и схем движения представлены в табл. 2.1:
Таблица 2.1
Время рейсов судов, (сутки)
№ типа судна |
Схемы движения |
Итого по судам |
||||
1 |
2 |
3 |
4 |
|||
1 |
185 |
61 |
115 |
93 |
454 |
|
2 |
180 |
73 |
116 |
92 |
461 |
|
Итого по схемам |
365 |
134 |
231 |
185 |
915 |
|
б) инвалютный доход судна i – го типа на j – ой схеме движения за один рейс (тыс. долл.) определяется по формуле:
Fij=∑fl qil (i = ; j = ), (2)
где fl – тарифная ставка на l-ом участке, долл./т;
qil - загрузка судна i – го типа на l-ом участке , тыс. т;
F11 - инвалютный доход судна 1-го типа на 1-й схеме:
F11 = f1*q11+ f4*q14+ f3*q13
F11 = 30*10+47*11+40*10=1217 (тыс. долл.).
Результаты расчета для остальных типов судов и схем движения представлены в табл. 2.2:
Таблица 2.2
Инвалютные доходы судов, (тыс. долл.)
№ типа судна |
Схемы движения |
Итого по суда |
||||
1 |
2 |
3 |
4 |
|||
1 |
1217 |
300 |
708 |
400 |
2625 |
|
2 |
1240 |
330 |
776 |
440 |
2786 |
|
Итого по схемам |
1457 |
630 |
1484 |
840 |
5411 |
|
в) расходы в инвалюте судна i – го типа на j – ой схеме движения за один рейс Rij принять равными 30 % от доходов в инвалюте.
Rij = 0,3* Fij (i = ; j = ) (3)
R11 – расход в инвалюте судна 1-го типа на 1-й схеме:
R11=0,3* F11
R11=0,3*1217=365,1 (тыс. долл.).
Результаты расчета для остальных типов судов и схем движения представлены в табл. 2.3:
Таблица 2.3
Расходы в инвалюте судов, (тыс. долл.)
№ типа судна |
Схемы движения |
итого по судам |
||||
1 |
2 |
3 |
4 |
|||
1 |
365,1 |
90 |
212,4 |
120 |
787,5 |
|
2 |
372 |
99 |
232,8 |
132 |
835,8 |
|
итого по схемам |
737,1 |
189 |
445,2 |
252 |
1623,3 |
|
2.3.Составление математической модели задачи.
При разработке математической модели задачи решаются следующие вопросы:
выбор параметров управления
выбор показателя качества (критерия оптимальности)
формирование ограничений и целевой функции в общем виде и с использованием конкретных числовых данных.
Выбор критерия оптимальности в расстановочной задаче существенно зависит от соотношения провозной способности флота П и объема перевозок Q. В курсовой работе П<Q, т.е. флота недостаточно для выполнения всех перевозок.
Критерий оптимальности – максимум чистой валютной выручки (ЧВВ).
∆ Fij = Fij - Rij (i = ; j = ).
∆ F11 – чистая валютная выручка судна 1-го типа на 1-й схеме:
∆ F11 = F11 – R11
∆ F11 = 1217-365,1=851,9 (тыс. долл.).
Результаты расчета для остальных типов судов и схем движения представлены в табл. 2.4:
Таблица 2.4
Чистые валютные выручки судов, (тыс. долл.)
№ типа судна |
Схемы движения |
Итого по судам |
|||
1 |
2 |
3 |
4 |
||
1 |
851,9 |
210 |
495,6 |
280 |
1837,5 |
2 |
868 |
231 |
543,2 |
308 |
1950,2 |
Итого по схемам |
1719,9 |
441 |
1038,8 |
588 |
3787,7 |
Математическая модель задачи в общем виде такова:
Z = ∑∑∆ Fij xij – max, (4)
∑∑qil
xij
≤
Ql
( ), (5)
), (5)
∑ tij xij = Ti (i= ), (6)
xij ≥ 0 (i= , j= ). (7)
где xij – число рейсов судов i – го типа на j – ой схеме движения, судорейсы;
Ti – бюджет времени в эксплуатации судов i – го типа, судо-сутки;
Ti = Ni*T (i= ), (5)
где Ni – число судов i – го типа;
T – продолжительность планового периода (Т=365 суток);
Т1=365*5=1825 судо–сут.;
Т2=365*6=2190 судо–сут.;
Ql – количество груза, предъявленное к перевозке на l-ом участке, тыс.т;
Gl – множество схем движения, содержащих l-ом участке,
S – количество груженых участков.
Экономический смысл:
целевой функции (4) – максимизировать чистую валютную выручку (ЧВВ);
ограничения (5) отражают требование: на каждом участке перевезти груз в количестве, не превышающем заявленного;
ограничения (6) отражают требование: использовать бюджет времени в эксплуатации судов всех типов на перевозках;
ограничения (7) – условие неотрицательности переменных.
Запишем математическую модель согласно исходным данным и построенным вариантам схем движения в координатной форме:
Целевая функция (1):
Z = ΔF11x11 + ΔF12x12 + ΔF13x13 + ΔF14x14 + ΔF21x21 + Δ F22x22 + ΔF23x23 +Δ F24x24 – max;
Ограничения (2):
q11 x11 + q11 x12 + q21 x21 + q21 x22 ≤ Q1, G1 = {1,4,3}
q12 x13 + q22 x23 ≤ Q2 , G2 = {1}
q13 x11 + q13 x13 +q13 x14 + q23 x21+ q23 x23 + q23 x24 ≤ Q3, G3 = {2,3}
q14 x11 + q24 x21 ≤ Q4; G4 = {3}
Ограничения (3):
t11 x11 + t12 x12 + t13 x13 + t14 x14 = T1
t21 x21 +t22 x22 + t23 x23 + t24 x24 = T2
Ограничения (4)
xij
≥
0 (i= ,
j=
,
j= ).
).
x11≥0; x12≥0; x13≥0; x14≥0 x21≥0; x22≥0; x23≥0; x24≥0
Подставим в математическую модель задачи в координатной форме значения нормативов, полученные ранее:
Целевая функция (1):
Z = 851,9x11 + 210x12 + 495,6x13 + 280x14 + 868x21 + 231x22 + 543,2x23 + 308x24 – max,
Ограничения (2):
10x11 + 10x12 + 11x21 + 11x22 ≤ 380,
11x13 + 12x23 ≤ 300,
10x11 + 10x13 + 10x14 + 11x21 + 11x23 + 11x24 ≤ 210,
11x11 + 10x21 ≤ 180;
Ограничения (3):
185x11 + 61x12 + 115x13 + 93x14 = 1825,
180x21 + 73x22 + 116x23 + 92x24 = 2190;
Ограничения (4):
xij ≥ 0 (i= , j= ).
x11≥0; x12≥0; x13≥0; x14≥0 x21≥0; x22≥0; x23≥0; x24≥0
Выпишем вектора условий:
А11
=
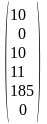 ;
А12 =
;
А12 =
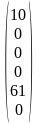 ;
А13
=
;
А13
=
 ;
А14
=
;
А14
=
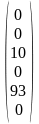 ;
;
А21
=
 ;
А22
=
;
А22
=
 ;
А23
=
;
А23
=
 ;
А24
=
;
А24
=
 .
.
Данная задача решается с помощью симплекс-метода, однако структурные ограничения не содержат нужного для построения базиса количества единичных векторов. Поэтому введем в математическую модель дополнительные и искусственные переменные, чтобы перейти от стандартной исходной задачи к канонической расширенной. Необходимо перейти к одноиндексным переменным, получаем, что: x11=x1, x12=x2, x13=x3, x14=x4, x21=x5, x22=x6, x23=x7, x24=x8. Таким образом, математическая модель примет вид:
Z = 851,9x1 + 210x2 + 495,6x3 + 280x4 + 868x5 + 231x6 + 543,2x7 + 308x8 0*S1+0*S2+0*S3+0*S4 – M*A5-M*A6 – max;
10x1+10x2+11x5+11x6 +S1 =380
11x3+12x7 +S2 =300
10x1+10x3+10x4+11x5+11x7+11x8 +S3 =210
11x1+10x5 +S4 =180
185x1+61x2+115x3+93x4 +A5 =1825
180x5+73x6+116x7+92x8 +A6 =2190
Xk
≥
0 (k= ).
).
x1≥0; x2≥0; x3≥0; x4≥0; x5≥0; x6≥0; x7≥0; x8≥0.
где S1, S2, S3, S4 – дополнительные переменные;
А5, А6 - искусственные переменные.
Мы получили 6 единичных векторов необходимых для построения базиса:
А9
=
 ;
А10 =
;
А10 =
 ;
А11
=
;
А11
=
 ;
А12
=
;
А12
=
 ;
А13
=
;
А13
=
 ;
А14
=
;
А14
=
 .
.
Исходный опорный план расширенной задачи:
X (x1=0; x2=0; x3=0; x4=0; x5=0; x6=0; x7=0; x8=0; S1=380; S2=300; S3=210; S4=180; A5=1825; A6=2190).
Формируем исходную симплекс-таблицу в табл. 2.5
Таблица 2.5
Исходная симплекс - таблица
№ |
Базис |
СБ. |
В |
851,9 |
210 |
495,6 |
280 |
868 |
231 |
543,2 |
308 |
0 |
0 |
0 |
0 |
– М |
– М |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
S1 |
S2 |
S3 |
S4 |
А5 |
А6 |
||||
1 |
S1 |
0 |
380 |
10 |
10 |
0 |
0 |
11 |
11 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
2 |
S2 |
0 |
300 |
0 |
0 |
11 |
0 |
0 |
0 |
12 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
3 |
S3 |
0 |
210 |
10 |
0 |
10 |
10 |
11 |
0 |
11 |
11 |
0 |
0 |
1 |
0 |
0 |
0 |
4 |
S4 |
0 |
180 |
11 |
0 |
0 |
0 |
10 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
5 |
А5 |
-М |
1825 |
185 |
61 |
115 |
93 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
6 |
А6 |
-М |
2190 |
0 |
0 |
0 |
0 |
180 |
73 |
116 |
92 |
0 |
0 |
0 |
0 |
0 |
1 |
m+1 |
Zij-Cij |
0 |
-851,9 |
-210 |
-495,6 |
-280 |
-868 |
-231 |
-543,2 |
-308 |
0 |
0 |
0 |
0 |
0 |
0 |
|
m+2 |
-4015 |
-185 |
-61 |
-115 |
-93 |
-180 |
-73 |
-116 |
-92 |
0 |
0 |
0 |
0 |
0 |
0 |
||
