Добавил:

kriiiiiiiiiisss Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный экономический университет (бывш. ФИНЭК, ИНЖЭКОН)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matematichexky_analiz

.docx

Скачиваний:

Добавлен:

08.01.2020

Размер:

8.2 Mб

Скачать

☆

Математичекский анализ

1. Определение монотонной функции. Необходимое и достаточное условие возрастания

функции. Достаточное условие строгого возрастания функции.

МОНОТОННАЯ ФУНКЦИЯ

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

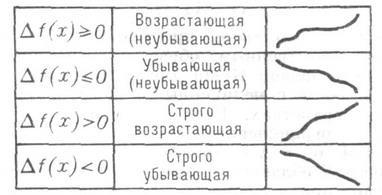
Если функция f в каждой точке нек-рого промежутка имеет производную, к-рая не меняет знака(соответственно сохраняет постоянный знак), то функция f монотонна (строго монотонна) на этомпромежутке.

Понятие М. ф. действительного переменного обобщается на функции различных классов.

http://mathematics.ru/courses/function/content/chapter1/section3/paragraph5/theory.html#.VXHyms_tmko

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) < f (x₂).

Функция f (x) называется убывающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) > f (x₂).

Достаточный признак монотонности.

f`(x)<0 – необходимый признак убывания функции.

Достаточное условие строгой монотонности функции на промежутке. Теорема (достаточное условие) Если функция f(x)дифференцируема на (a,b) и f/(x)≥0 (f/(x)≤0) на (a,b), то f(x) не убывает (не возрастает) на (a,b). Доказательство Рассмотрим случай когда f/(x)≥0 . Рассмотрим две точки x1,x2∈(a,b) и применим формулу ЛагранжаНа [x1,x2] функция f(x) удовлетворяет всем условиям этой теоремы. Следует, чтоx1<x2: f(x2)−f(x1)=f/(c)(x2−x1), где c∈(x1,x2) и правая часть больше нуля, значит f(x2)−f(x1)≥0 или f(x2)≥f(x1) при x2>x1, функция не убывает. Теорема доказана.

3. Определение локального экстремума функции одной переменной. Необходимое

условие локального экстремума функции одной переменной. С.172

4. Определение локального экстремума функции одной переменной. Первое доста-

точное условие строгого локального экстремума функции одной переменной.

5. Определение локального экстремума функции одной переменной. Второе доста-

точное условие строгого локального экстремума функции одной переменной.

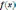
Функция приимеет минимум, если найдется такая дельта окрестность этой точки, что для всех x принадлежащих этой дельта окрестности будет выполняться условие . ()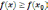

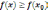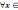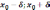
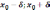Общим названием для максимума и минимума служит термин – экстремум. Прифункция имеет экстремум, если в этой точке она имеет или максимум, или минимум.

Через производную формулируются необходимые и достаточные условия для того, чтобы функция в точке имела экстремум.

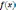
Необходимое условие экстремума - Если функция 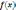имеет при некотором экстремум и если она дифференцируема в этой точке, то необходимо в этой точке будет выполняться соотношение .

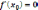Пусть х₀ – критическая (стационарная) точка функции y = f(x) (т.е. внутренняя точка области ее определения, в которой производная равна нулю). Тогда можно сформулировать следующие достаточные условия существования экстремума в этой точке:

а) Пусть функция дифференцируема в некоторой окрестности U точки х₀, не содержащей других критических точек. Тогда:

 если при переходе через точку х₀ производная f ' меняет свой знак с плюса на минус, х₀ – точка (локального) максимума функции;

 если при переходе через точку х₀ производная меняет свой знак с минуса на плюс, х₀ – точка (локального) минимума функции;

 если при переходе через точку х₀ производная не меняет свой знак, в точке х₀ нет экстремума.

б) Пусть в точке х₀ существует вторая производная функции f, f ''(x0), не равная нулю. Тогда:

 если f’’(x₀) > ₀, х₀ – точка (локального) минимума функции;

 если f’’(x₀) < ₀, х₀ – точка (локального) максимума функции.

6. Определение выпуклости и вогнутости функции одной переменной (выпуклость

вверх и выпуклость вниз). Достаточное условие выпуклости функции одной пере-

менной. С. 176

График функции f(x) на данном промежутке 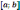обращен выпуклостью вверх (вниз) если любая точка графика функции лежит ниже (выше) соответствующей точки любой касательной, проведенной к графику функции на этом промежутке (кроме точки касания).

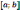
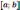
Достаточное условие:Теорема - Если в каждой точке промежутка 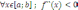, тогда график функции на этом промежутке будет обращен выпуклостью вверх. Критерий вогнутости функции на промежутке 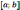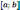. Если в каждой точке промежутка 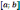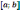выполняется соотношение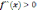, то в этом случае функция будет вогнута на данном промежутке, график будет обращен выпуклостью вниз.

http://stu.sernam.ru/book_msh.php?id=154

7. Определение точки перегиба графика функции одной переменной. Необходимое

условие перегиба.http://edu.alnam.ru/book_man_b.php?id=113

8. Определение точки перегиба графика функции одной переменной. Достаточное

условие перегиба. С.177

Определение. Точка М(с;f(с) графика функции y=f(x) называется точкой перегиба этого графика, если существует такая окрестность точки с оси абсцисс, в пределах которой график функции y=f(x) слева и справа от с имеет разные направления выпуклости.Y=f(x) дифференцируема на интервале (a;b) и с принадлежит (a;b).

Теорема (необходимое условие точки перегиба)

Если точка — точка перегиба функции и если в некоторой окрестности точки (непрерывная в точке ), то .

Доказательство

Докажем методом от противного, т.е предположим, что . Тогда либо . По условию непрерывна в точке по свойству сохранения знака непрерывной функции получим: : , , т.е по достаточному условию строгой выпуклости (функция выпукла вниз) или (функция выпукла вверх). Это противоречит определению точки перегиба, которое гласит, что при переходе через точку направление выпуклости меняется.

Теорема (достаточное условие точки перегиба)

Если функция непрерывна в точке и имеет в этой точке конечную или бесконечную производную и если меняет знак при переходе через точку , то точка — точка перегиба функции .

Доказательство

Пусть меняет знак с «-» на «+», тогда по достаточному условию строгой выпуклости функция на интервале функция будет строго выпукла вверх, на интервале — строго выпукла вниз, т.е при переходе через точку направление выпуклости изменяется по определению — точка перегиба.

Пример:

Найти точки перегиба функции .

Решение:

Найдем вторую производную функции: , значит . Найдем промежутки знакопостоянства функции. При переходе через точку функция изменяет направление выпуклости, значит — точка перегиба графика функции.

9.Определение вертикальной и наклонной асимптоты. Теорема о наклонной асимп-

тоте.

10. Наибольшее и наименьшее значение функции одной переменной на замкнутом промежутке. С. 175

Наибольшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Наименьшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Правило нахождения наибольшего и наименьшего значения на (a; b):

Найти критические точки функции (a;b)
Вычислить значения функции в найденных критических точках;
Вычислить значения функции на концах отрезка, т.е. в точках х=а; х=b;
Среди всех вычисленных значений функции выбрать наибольшее и наименьшее.

Замечание: 1. Если критическая точка одна и она является максимумом( минимумом), то в этой функции она принимает наиб. ( наим.) значение.

2. Если функция не имеет критических точек, это значит, что функция монотонно возрастает или убывает. Следовательно наиб. И наим. Значение принимает на концах промежутка.

11. Формула Тейлора и формула Маклорена. С. 182

http://mathprofi.ru/razlozhenie_funkcij_v_stepennye_ryady.html

Если функция в некотором интервале раскладывается в степенной ряд по степеням , то это разложение единственно и задается формулой:

Примечания: надстрочный индекс в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву .

Данная формула носит фамилию англичанина Тейлора (ударение на первый слог).

На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда :

Этот ряд получил известность благодаря шотландцу Маклорену (ударение на второй слог). Разложение Маклорена также называют разложением Тейлора по степеням .

Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции: Как оно получилось? По формуле Маклорена: Рассмотрим функцию , тогда:

Теперь начинаем находить производные в точке ноль: первую производную, вторую производную, третью производную и т.д. Это просто, поскольку при дифференцировании экспонента превращается в саму себя: