
МАТАННН
.docx20. Определение градиента функции, поверхность уровня, свойства градиента.
Определение. Градиентом функции многих переменных в данной точке называется вектор, координаты которого равны частным производным по соответствующим аргументам, вычисленным в данной точке.
![]() .
.
Градиент функции есть вектор, направление которого указывает направление наибыстрейшего возрастания функции, а модуль равен наибольшей скорости изменения функции в определённой точке.

Свойста:
Для любого постоянного числа ![]() и
скалярных полей
и
скалярных полей ![]() справедливо
следующее:
справедливо
следующее:
![]()
Линейность
![]()
![]()
Правило Лейбница
![]() ,
где
,
где ![]() — скалярное
произведение векторов
— скалярное
произведение векторов ![]() и
и ![]()
. 21. Числовые ряды. Сходимость. Признаки сходимости:
интегральный ,Даламбера, сравнение.
Пусть
мы имеем числовую последовательность ![]() ,
где
,
где ![]() .
.
Приведем
пример числовой последовательности: ![]() .
.
Числовой
ряд –
это сумма членов числовой последовательности
вида ![]() .
.
В
качестве примера числового ряда можно
привести сумму бесконечно убывающей
геометрической прогрессии со знаменателем q
= -0.5:  .
.
![]() называют общим
членом числового ряда или k–ым членом
ряда.
называют общим
членом числового ряда или k–ым членом
ряда.
Для
предыдущего примера общий член числового
ряда имеет вид  .
.
Частичная
сумма числового ряда –
это сумма вида ![]() ,
где n –
некоторое натуральное число.
,
где n –
некоторое натуральное число. ![]() называют
также n-ой частичной
суммой числового ряда.
называют
также n-ой частичной
суммой числового ряда.
Числовой
ряд ![]() называется сходящимся,
если существует конечный предел
последовательности частичных сумм
называется сходящимся,
если существует конечный предел
последовательности частичных сумм ![]() .
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд
.
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд ![]() называется расходящимся.
называется расходящимся.
Суммой
сходящегося числового ряда ![]() называется
предел последовательности его частичных
сумм, то есть,
называется
предел последовательности его частичных
сумм, то есть, ![]() .
.
Числовой
ряд ![]() называется знакоположительным,
если все его члены положительны, то
есть,
называется знакоположительным,
если все его члены положительны, то
есть, ![]() .
.
Числовой
ряд ![]() называется знакочередующимся,
если знаки его соседних членов различны.
Знакочередующийся числовой ряд можно
записать в виде
называется знакочередующимся,
если знаки его соседних членов различны.
Знакочередующийся числовой ряд можно
записать в виде ![]() или
или ![]() ,
где
,
где ![]() .
.
Числовой
ряд ![]() называется знакопеременным,
если он содержит бесконечное множество
как положительных, так и отрицательных
членов.
называется знакопеременным,
если он содержит бесконечное множество
как положительных, так и отрицательных
членов.
Знакопеременный
ряд ![]() называется абсолютно
сходящимся,
если сходится ряд из абсолютных величин
его членов, то есть, сходится
знакоположительный числовой ряд
называется абсолютно
сходящимся,
если сходится ряд из абсолютных величин
его членов, то есть, сходится
знакоположительный числовой ряд ![]()
Знакопеременный
ряд ![]() называется условно
сходящимся,
если ряд
называется условно
сходящимся,
если ряд ![]() расходится,
а ряд
расходится,
а ряд ![]() сходится.
сходится.
Необходимое условие сходимости ряда.
Если
числовой ряд ![]() сходится,
то предел его k-ого члена
равен нулю:
сходится,
то предел его k-ого члена
равен нулю: ![]() .
.
Первый признак сравнения рядов.
Пусть ![]() и
и ![]() -
два знакоположительных числовых ряда
и выполняется неравенство
-
два знакоположительных числовых ряда
и выполняется неравенство ![]() для
всех k
= 1, 2, 3, ... Тогда
из сходимости ряда
для
всех k
= 1, 2, 3, ... Тогда
из сходимости ряда ![]() следует
сходимость
следует
сходимость ![]() ,
а из расходимости ряда
,
а из расходимости ряда ![]() следует
расходимость
следует
расходимость ![]() .
.
Признак Даламбера.
Пусть ![]() -
знакоположительный числовой ряд. Если
-
знакоположительный числовой ряд. Если ![]() ,
то числовой ряд сходится, если
,
то числовой ряд сходится, если ![]() ,
то ряд расходится.
,
то ряд расходится.


22. Определение локального экстремума ФМП. Необходимое условие экстремума
ФМП.
Точка х0;у0
называется точкой максимума функции
z=f(x;y),
если существует такая дельта окрестность
точки х0;у0, что для каждой точки х;у,
отличной от х0;у0 из этой окрестности
выполняется неравенство f(x;y)<f(x0;y0).

23. Определение локального экстремума ФНП. Достаточное условие экстремума
ФМП
Точка х0;н0 называется точкой максимума функции z=f(x;y), если существует такая дельта окрестность точки х0;у0, что для каждой точки х;у, отличной от х0;у0 из этой окрестности выполняется неравенство f(x;y)<f(x0;y0).


24. Условный экстремум функции двух переменных .

25. Наибольшее и наименьшее значение ФМП в замкнутой и ограниченной области.


26 Производная от функции заданной неявно. Примеры.


27. Определение первообразной функции. Теоремы о свойствах первообраьтзных функций.


28.Определение неопределенного интеграла. Теорема о существовании неопределенного интеграла (достаточное условие).
.
29Таблица
интегралов
30Свойства
неопределенного интеграла
 .
.
31 Метод замены переменной (метод подстановки) в неопределенных интегралах.

32. Метод интегрирования по частям в неопределенном интеграле.

33 Определенный интеграл (определение, геометрический смысл).




34 Свойства определенного интеграла






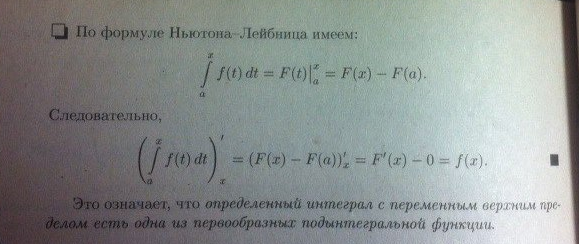
35Формула
Ньютона-Лейбница

36 Метод замены переменной (метод подстановки) в определенных интегралах.


37 Метод интегрирования по частям в определенном интеграле.


38 Определение несобственного интеграла первого рода (по бесконечному промежутку).



39 Определение несобственного интеграла второго рода (от функций, имеющих разрыв).


40.Cтепенные ряды. Радиус сходимости
Степенным рядом называется функциональный ряд вида
 (1.1) где a0, a1, a2,
…,an,…,
а также x0 –
постоянные числа. Точку x0 называют
центром степенного ряда.
(1.1) где a0, a1, a2,
…,an,…,
а также x0 –
постоянные числа. Точку x0 называют
центром степенного ряда.
Для
каждого степенного ряда  существует
существует ![]() ,
удовлетворяющее свойствам:
,
удовлетворяющее свойствам:
-
Если
 ,
то ряд сходится только при
,
то ряд сходится только при 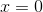 .
. -
Если
 ,
то ряд сходится при любых
,
то ряд сходится при любых 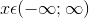 .
. -
Если
 ,
то ряд сходится при
,
то ряд сходится при  и
расходится при
и
расходится при 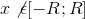 .
.
Сходимость
на любом отрезке внутри интервала![]() равномерная.
равномерная.
Число ![]() - радиус
сходимости степенного
ряда.
- радиус
сходимости степенного
ряда.
Утверждение о равномерной сходимости.
Если![]() ,
то в точке
,
то в точке ![]() ряд
сходится, следовательно, по теореме
Абеля он сходится равномерно на
ряд
сходится, следовательно, по теореме
Абеля он сходится равномерно на ![]() .
.
![]()
