При равенстве "левого" и "правого" грузооборотов пробной точки (числами указан грузооборот потребителей, тонн в месяц)

Для определения методом пробной точки оптимального узла транспортной сети прямоугольной конфигурации, с целью размещения в нем распределительного склада, сле­дует нанести на карту района координатные оси, сориенти­рованные параллельно дорогам. Определив координаты по­требителей, необходимо на каждой координатной оси най­ти методом пробной точки оптимальное место расположе­ния координаты X и координаты Y искомого узла.

В качестве примера рассмотрим обслуживаемую сис­тему, состоящую из четырех потребителей (рис. 3.29; справа от потребителей указан месячный объем завоза). Сеть дорог прямоугольная. Присваивая ординатам и абсциссам потребителей соответствующие значения объема завоза, найдем методом пробной точки ординату и абсциссу опти­мального узла транспортной сети. Размещение распреде­лительного склада в найденном узле обеспечит минималь­ное значение грузооборота транспорта по доставке това­ров в магазины.

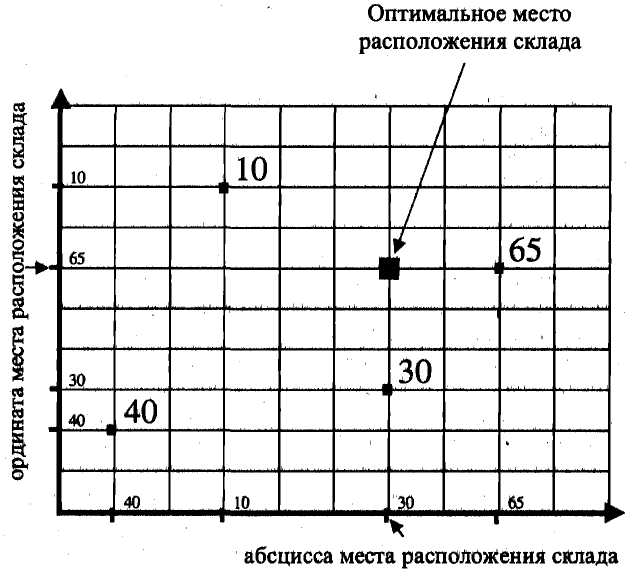
Точками на схеме обозначены потребители материального потока, числами — величины грузооборота потребителей, тонн в месяц

Рис 3.29. Определение места расположения склада в условиях прямоугольной конфигурации сети автомобильных дорог

Г. Метод математического моделирования

В подобной ситуации необходимо решить задачу распределения сфер обслуживания (торговых зон) РСЦ (распределительных складских центров) и их размещения на полигоне обслуживания.

Графическое изображение данной задачи представлено на рис.4.3. На этой схеме и в задаче применены следующие обозначения:

─ пункты производства продукции;

─ распределительные складские центры (РСЦ);

─ потребители продукции;

─ грузопотоки от i-ого производителя до j-ого РСЦ;

─ грузопотоки от j-ого РСЦ до k-ого потребителя;

X_j ─ количество хранимого и перерабатываемого груза в j-ом РСЦ;

C_j ─ стоимость хранения и переработки единицы груза в j-ом РСЦ;

P_i ─ количество продукции, поступающей на магистральный транспорт от i-оro производителя;

Q_k ─ потребность k-ого получателя в продуктах;

C_ij и C_jk ─ стоимость перемещения единицы продукции соответственно из пункта производства i в j-й РСЦ и из j-ого РСЦ в пункт потребления k.

С учетом принятых обозначений экономико-математическая модель решения задачи распределения материальных потоков между РСЦ формулируется следующим образом:

^.

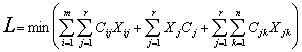Целевая функция выражает суммарные затраты, связанные с транспортировкой и переработкой грузов в РСЦ.

Задача заключается в нахождении таких X_ij и X_jk, которые минимизируют целевую функцию при следующих ограничениях:

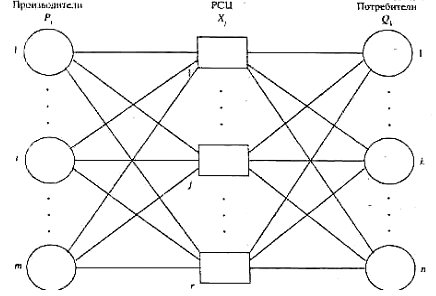
Рис. 4.3. Схема полигона, на котором осуществляются оптимальное размещение РСЦ и разделения потоков между ними

Данная модель может иметь ряд модификаций. В приведенной форме решается задача оптимального распределения грузопотоков между региональными центрами. В модель могут быть внесены ограничения по перерабатывающей способности технических средств РСЦ, провозной способности отдельных направлений транспорта и т. д. Если помимо распределения потоков необходимо оптимизировать размещение и определить количество региональных центров на полигоне, то тогда помимо производственно-транспортной задачи решается комбинаторная задача (на основе перебора вариантов или методом динамического программирования).