Дифракция света

Прямолинейность распространения света в однородной среде настолько привычна, что кажется самоочевидной. Прямолинейность света легко объяснить, исходя из представлений о свете, как о потоке световых корпускул. Однако с точки зрения света в волновой теории эта прямолинейность не является столь очевидной. Опыты показали, что закон прямолинейности распространения света не является универсальным. Он нарушается при прохождении света сквозь достаточно узкие щели и отверстия, а также при освещении небольших непрозрачных препятствий. При этом на экране, установленном позади отверстия или препятствия, вместо четко обозначенных областей света и тени наблюдаются системы интерференционных максимумов и минимумов. Такие явления, возникающие при распространении света в среде с резко выраженными неоднородностями, получили название дифракции света.

ПРИНЦИП ГЮЙГЕНСА

К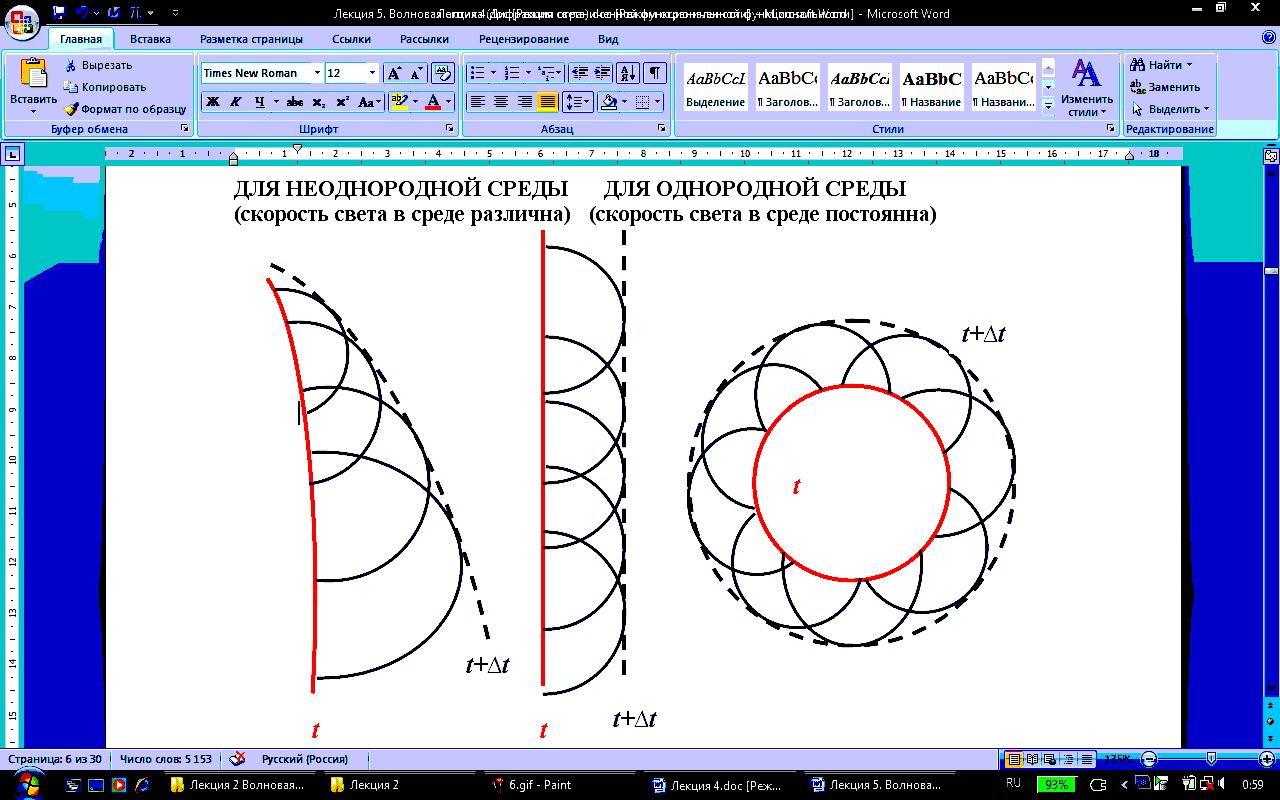 ачественное поведение света за преградой может быть объяснено с помощью принципа Гюйгенса, который позволяет установить способ построения фронта волны в момент времени по известному положению фронта в момент времени t. Согласно принципу Гюйгенса, каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн даёт положение фронта волны в следующий момент времени.

В такой постановке принцип Гюйгенса говорит лишь о направлении распространения волнового фронта. Речь идёт собственно о распространении этой поверхности, а не о распространении волн. В этих условиях принцип Гюйгенса позволяет вывести основные законы геометрической оптики – законы преломления и отражения.

П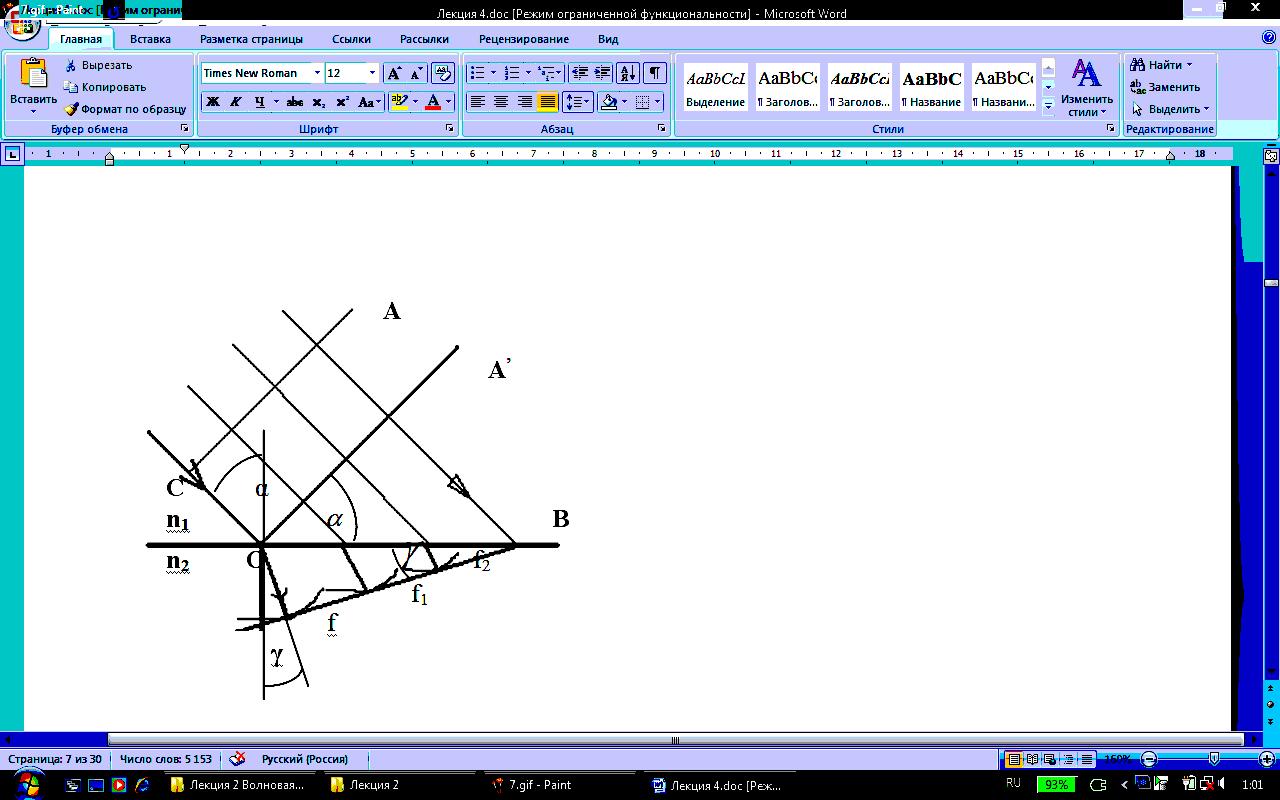 усть – скорость распространения волны в первой среде, – скорость распространения волны во второй, – угол между перпендикуляром к фронту волны и перпендикуляром к поверхности преломляющей среды. В момент t=0 точка С фронта волны достигла преломляющей среды и совпала с точкой О. Тогда за время точка фронта волны достигла в точке В границы раздела. Из точки О, как из центра, вторичная волна распространяется на расстояние Of. По принципу Гюйгенса действительное положение волнового фронта указывается огибающей элементарных волн – плоскостью . Из рисунка видно, что . Очевидно, что . Подставляя , , получаем: . Отсюда следует: – закон преломления света.

Рассмотрим отражение света. Подобно предыдущему: ,

– закон отражения света.

ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ

Принцип Гюйгенса не даёт никаких указаний об интенсивности волн, распространяющихся в различных направлениях. Этот недостаток был устранен Френелем.

Во-первых: следуя Гюйгенсу, Френель считал, что при распространении волн, создаваемых источником S_О, можно заменить источник эквивалентной ему системой вторичных источников и возбуждаемых ими вторичных волн. В качестве этих источников можно выбрать малые участки любой замкнутой поверхности S, охватывающей S_О.

Во-вторых: Френель предположил, что вторичные источники когерентны между собой, поскольку эквивалентны одному и тому же источнику S_О. Поэтому в любой точке вне вспомогательной поверхности S волны, реально распространяющиеся от источника S_О, должны являться результатом интерференции всех вторичных волн.

В-третьих: Френель предположил, что для поверхности S, совпадающей с волновой поверхностью, мощности вторичного излучения равных по площади участков одинаковы. Кроме того, каждый вторичный источник излучает свет преимущественно в направлении внешней нормали . Наконец, Френель предполагал, что в том случае, когда часть поверхности S покрыта непрозрачными экранами, вторичные волны излучаются только открытыми участками поверхности S.

ОБЪЯСНЕНИЕ ПРЯМОЛИНЕЙНОСТИ РАСПРОСТРАНЕНИЯ СВЕТА

ПО ВОЛНОВОЙ ТЕОРИИ

И сходя из принципа Гюйгенса-Френеля, легко получить закон прямолинейности распространения света в свободной от препятствий однородной среде.

На рисунке R – радиус сферической волновой поверхности (R<S_ОM), где M – произвольная точка, в которой нужно найти амплитуду световых колебаний E. Искомая амплитуда зависит от результата интерференции вторичных волн.

О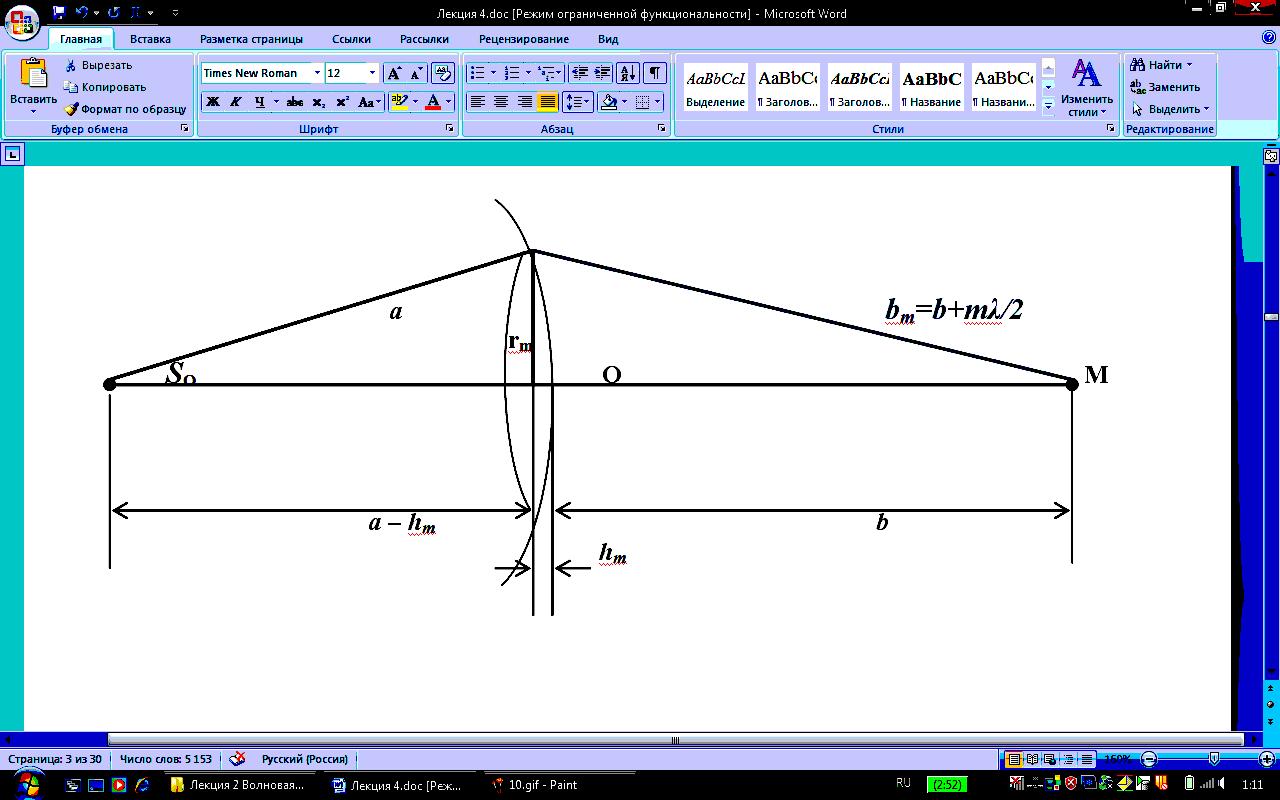 бщее решение сложно, однако Френель предложил оригинальный метод разделения поверхности S на зоны, позволяющие сильно упростить решение (метод зон Френеля): разобьём изображенную на рисунке волновую поверхность на кольцевые зоны, построенные так, что расстояние от краёв каждой зоны до точки M отличаются на ( – длина волны).

Вычислим площади зон:

, где S_m и S_m-1 – площади круговых сегментов.

; (величины взаимно уничтожаются). Из предыдущего выражения получаем:

(ввиду малости ).

Отсюда: . Тогда площади сфер S_m и S_m-1, используя известное выражение для их нахождения, определяются по формулам:

Используя полученные выражения, находим площадь сферического сегмента как разность площадей сфер S_m и S_m-1:

– из этой формулы следует, что площадь сегмента не зависит от m, т.е. площади различных сегментов одинаковы, а это означает, что мощности излучения вторичных волн с каждого сегмента равны.

Подставив h_m в выражение для r_m², получаем: .

Из полученных результатов можно сделать следующий вывод: так как и угол между нормалью к поверхности сегмента и ) растет, то амплитуда световых колебаний E_m уменьшается монотонно: E₁ > E₂ > … > E_m-1 > E_m > E_m+1. Фазы колебаний, возбуждаемых соседними зонами отличаются на – т.е. источники вторичных волн, находящиеся на соседних зонах, излучают волны в противофазе. Поэтому:

Вследствие монотонности: С учетом этого: . Из полученного результата следует, что если оставить только центральную зону открытой, то амплитуда световой волны возрастет в 2 раза, а интенсивность световой волны – в 4 раза (поскольку интенсивность ~ E²).

Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или нечетные зоны, то интенсивность света в точке М резко возрастет. Такая пластинка называется зонной пластинкой.