2. Структура передаваемого ofdm - сигнала.
Для анализа метода синхронизации необходимо рассмотреть формальное описание передаваемого OFDM-сигнала. Полезная часть передаваемого OFDM-символа по свойству дискретного преобразования Фурье (ДПФ) может быть представлена в виде
,
(1)
где
- комплексная амплитуда,
- длительность символа без защитного
интервала,
;
- период дискретизации;
- расстояние по частоте между гармониками;
- количество отсчетов в ДПФ. До полезной
части передаётся защитный интервал
длительностью
,
который является её периодическим
повторением, при этом
- длительность символа после введения
защитного интервала.
.
На рис. 2 представлена структура
OFDM-символа.
Для символа целесообразно выполнение
условия
,
т.е.
,
поскольку в системе локации более важно
обнаружение, нежели распознавание.
Рис. 2. структура OFDM-символа.
Поскольку
последовательно передаются две одинаковые
части длиной
,
то переданный сигнал имеет вид
,
(2)
3. Искажения принятого сигнала относительно излучённого.
Согласно [2, 6] с учётом выражения (1) представим принятый сигнал на входе приёмника в виде:
,
(3)
,
где
- задержка передаваемого сигнала,
складывающаяся из времени распространения
в среде и групповой задержки, получающейся
прохождением через тракты обработки
сигнала;
- импульсная характеристика (ИХ) канала
распространения. Доплеровский сдвиг
сигнала по частоте возникает вследствие
относительного движения и равен
,
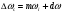где
- сдвиг частоты на целое количество
гармоник, а
- сдвиг сигнала по частоте на значение,
которое не превосходит
.
При этом
- аддитивный гауссовский белый шум (БШ).
Знак «
»
в формуле (3) означает свёртку сигналов.
В дискретном представлении сигнала (3) имеет вид
,
(4)
,
где
.
Поскольку
для системы локации, где
,
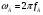а
- доплеровская частота, то
в формуле (4).
Тогда из (2) и (4) получим
,
где
,
а также
.
(5)
Таким образом,
реализация принятого сигнала
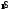состоит из двух частей, а именно
и
,
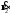которые являются реакцией ИХ канала на
защитную и полезную части вектора
соответственно, т.е.
,
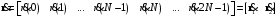(6)
где
,
,
,
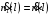а
,
,
,
Стоит отметить,
что в соответствии с (5) и (6) для любого
отсчёта
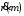выполняется равенство
,
(7)
где
,
- мощности сигнала и шума соответственно,
а
- оператор усреднения. Равенство
при
выполняется, поскольку в соответствии
с (1) спектр сигнала занимает всю полосу
частот от 0 до
,
т.е. интервал дискретизации
равен интервалу корреляции по свойству
преобразования Фурье. При этом условие
выполняется для любого отсчёта реализации.
4. Алгоритм обнаружения.
Для синтеза
соотношений, определяющих задержку до
цели и доплеровский сдвиг [7], используем
корреляционные свойства сигнала во
временной области. Согласно (6) рассмотрим
произвольный отрезок реализации
принятого сигнала в виде набора дискретных
отсчётов, который начинается с номера
,
т.е.
.
(8)
Запишем совместную
плотность распределения вероятностей
(ПРВ) отсчётов вектора (3) в соответствии
с равенством (4) в случае синхронизации,
т.е. когда
представляет собой один полный символ,
получим
.
При этом распределения
доплеровского сдвига
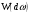и задержки до цели
являются априорно неизвестными, поэтому
их можно опустить, тогда получим
.
(9)
В этом случае ПРВ
состоит из
произведений ПРВ попарно коррелированных
отсчётов полезной части символа и
защитного интервала, т.е.
.
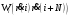Согласно (3) обозначим
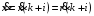- отсчёт входного сигнала в момент
времени
,
а
- отсчёт входного сигнала, который
поступил на
позже. Сигнал комплексный, поэтому ПРВ
для
и
в случае нормального распределения
шума
в формуле (3) согласно [3] примет вид:
,
(10)
где
- ковариационная матрица.
При этом
,
где коэффициент корреляции, согласно
условию (7) равен
.
После упрощений получим
.
(11)
В дальнейшем будем
рассматривать случай преобладания
сигнала над шумом, т.е.
.
Определим функцию правдоподобия (ФП)
как логарифм
,
т.е.
,
(11)
тогда
,
(12)
где
- корреляционная сумма на интервале
длиной
,
причём
,
и
- энергетическая составляющая сигнала
на интервале длиной
.
Тогда условие максимума ФП представляет собой систему уравнений
,
что равносильно выполнению условия
.
(17)
Поскольку
можно считать постоянной и независимой
от
в соответствии с (7), то условие (17) можно
представить в виде:
.
(18)
Таким образом, получена максимально правдоподобная оценка сдвига отражённого сигнала по времени и частоте. На рис. 4. представлена функциональная схема [8], реализующая описанный алгоритм.
Рис. 4. Функциональная схема, реализующая алгоритм определения грубой временной задержки и точного частотного сдвига. Обозначения: ( )*-комплексное сопряжение; abs и arg – вычислители абсолютного значения и аргумента комплексной величины соответственно; argmax – вычислитель аргумента максимального значения.
Из условия (18) получим радиальную скорость цели и дальность до цели
,
(18)
где
- длина волны Грч
на рис. 1.
Основным недостатком
алгоритма (18) является тот факт, что не
используется знание априорно известного
сигнала
,
однако это же является достоинством,
поскольку для обнаружения не требуется
учитывать искажения сигнала, описанные
в формуле (3).