3. Методические указания по проведению работы

3.1. Получите у преподавателя допуск к проведению данной работы.

3.2.Соберите измерительную цепь согласно вычерченной в тетради схеме (рис. 4 ,а), используя на стенде в качестве резистор = 3 кОм, а в качестве емкости С - емкость конденсатора С_А = 25 нФ.

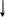
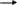
а).

б).

Рис. 4 – Схема цепи синусоидального тока с емкостным элементом а) – с обычным подключением клемм генератора б) – с противоположным подключением клемм генератора.

Показанное соединение вольтметра и фазометра позволяет производить измерения напряжения и его фазового сдвига на резисторе исследуемой цепи, а также определять ток цепи и его фазовый сдвиг.

3.3.Генератор стенда включите в режиме ГСС (синусоидальная форма напряжение варьируемой частоты "f-var").

3.4.Поддерживая по вольтметру напряжение на генераторе 0,8В и контролируя по осциллографу синусоидальный характер этого напряжения, увеличивайте от возможного минимального значения частоту генератора до такого значения , при котором напряжение на резисторе (по вольтметру ) возрастет до значения 0,4 В. Запишите найденное значение частоты в лабораторную тетрадь. Измерьте по фазометру сдвиг фаз между напряжением резистора (и, "опорным" напряжением генератора, который совпадает со сдвигом Фаз между током и напряжением генератора: Значит аргумент комплексного сопротивления собранной на стенде цепи, который определяется как сдвиг фаз между входным напряжением и током, равен Запишите в тетрадь найденные значения этих углов.

3.5.Подсчитайте по значениям , и значения и .

3.6.Переключите входные зажимы собранной на стенде цепи к противоположным выходным клеммам генератора, как показано на рис. 4,б). При этом, очевидно, режим цепи не изменится, но только вольтметр будет показывать напряжение на конденсаторе, а фазометр – сдвиг фаз между напряжением на конденсаторе и "опорным" напряжением генератора: .

3.7.Измерьте по фазометру последний сдвиг фаз и по вольтметру – напряжение на конденсаторе. Запишите измеренные значения в тетрадь. Если можно пренебрегать потерями в конденсаторе, то разность измеренных углов должна оказаться равной + 90°. При заметных потерях в конденсаторе эта разность будет меньше, хотя и должна оставаться положительной. Подсчитайте рассмотренную разность углов по полученным результатам их измерения фазометром.

3.8.По результатам измерений постройте в одинаковом масштабе три векторные диаграммы тока и напряжений цепи: 1) в предположении, что начальная фаза напряжения генератора равна нулю; 2) в предположении, что она равна 180°.

3.9.По результатам проведенных измерений подсчитайте и конденсатора вашего стенда.

4. Некоторые пояснения

4.1. Синусоидальное напряжение при заданной круговой частоте О) полностью определяется своими действующим значением и начальной фазой

(2.1)

Поэтому полную информацию об этом синусоидальном напряжении заданной частоты содержит комплексное напряжение (комплексное действующее значение напряжения):

(2.2)

Аналогично определяются комплексное напряжение

(2.3)

и комплексный ток

2.4)

Иногда комплексные напряжение и ток называют просто комплексами напряжения и тока.

В теории цепей часто вместо действующего значения применяют амплитудное значение синусоидальных величин. Например, и – амплитуды двух напряжений, – амплитуда тока. Соответственно определяются и комплексные амплитуды напряжений и токов:

(2.5)

(2.6)

(2.7)

Будем называть сдвигом фаз между синусоидальными напряжениями и разность фаз этих напряжений с определенным знаком “+” или “-“:

(2.8)

Сдвиг фаз в пределах от до между двумя синусоидальны­ми напряжениями (первое из которых условимся называть "измеряемым'', а второе – "опорным") может быть измерен фазометром. У фазометра, применяемого в нашем лабораторном стенде, может быть измерен сдвиг фаз между двумя синусоидальными потенциалами двух точек схемы – "измеряемым" и "опорным" (или "И" и "О"), причем знак измеренного угла определяется по одному из двух светодиодов: минусу соответствует зажигание левого светодиода, помеченного "I", а плюсу – правого, помеченного "С". Предполагается, что с точкой измеряемого потенциала соединен правый вход "Измер." фазометра, а с точкой опорного потенциала соединен левый вход "Опорн." фазометра.

4.2. Аналогично, сдвигом фаз между напряжением и током

(2.9)

(3.1)

будем называть следующий фазовый сдвиг:

(3.2)

Если комплексное напряжение пропорционально комплексному току линейного двухполюсника, то взаимообратные отношения этих комплексов называют комплексным сопротивлением и комплексной проводимостью этого двухполюсника:

(3.3)

(3.4)

Модули комплексного сопротивления и комплексной проводимости принято называть соответственно полным сопротивлением и полной проводимостью, а угол называют аргументом комплексного сопротивления.

4.3. Комплексные сопротивление и проводимость иногда представляют в алгебраической форме:

(3.5)

(3.6)

где – активная составляющая сопротивления, – активная состав­ляющая проводимости, – реактивная составляющая сопротивления и – реактивная составляющая проводимости.

Параметры алгебраического представления и полярной формы комплексных сопротивления и проводимости связаны известными соотношениями:

(3.7)

(3.8)

4.4. Комплексное сопротивление идеального резистора является вещественным (его аргумент равен нулю или, при отрицательном сопротивлении резистора, – ±180°).

4.5. Комплексное сопротивление емкости является чисто мнимым числом с аргументом -90° (или +90° , когда емкость является отрицательной. Отрицательные компоненты цепи: сопротивления, емкости и т. п. – это сложные активные устройства, требующие для своего функционирования источников питания. Например, они могут быть реализованы с помощью конвертора отрицательного сопротивления.

(3.9)

Здесь – емкостное сопротивление, которое обратно пропорционально частоте:

(4.1)

Не путайте емкостное сопротивление и реактивное сопротивление , которое у емкости обратно по знаку емкостному сопротивлению:

т. е., положительная емкость имеет отрицательное реактивное сопротивление .

4.6. Емкость обычно реализуется емкостью конденсатора. Реальный конденсатор имеет потери, которые иногда учитываются простейшими последовательной или параллельной схемами замещения (рис. 5, а и б), в которых потери учитываются сопротивлениями потерь или

а) б)

Рис 5 – Схемы замещения конденсатора: а) – последовательная, б) – параллельная .

При этом емкость и сопротивление потерь таких схем зависят частоты.

Последнее затрудняет анализ соответствующих цепей в широком диапазоне частот.

Поэтому, были найдены квазиэквивалентные схемы, которые достаточно точно реализуют характеристики реального конденсатора в широком диапазоне частот.

Одна из таких схем (рис. 6) с тремя независящими от частоты параметрами , и обычно достаточно точно передает свойства реальных конденсаторов в диапазоне радиочастот.

Последняя, схема наиболее часто применяется при численном моделировании частотных характеристик электрических цепей с конденсаторами.

В диапазоне сверхвысоких частот в последнюю схему замещения реального конденсатора иногда добавляют индуктивные элементы, позволяющие учесть индуктивность проводников конденсатора.

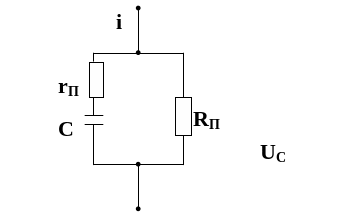
Рис. 6 – Схема квазиэквивалентная с тремя независящими от частот параметрами .

4.7. При анализе экспериментальной цепи рис. 4 наиболее удобно воспользоваться последовательной схемой замещения конденсатора (рис. 7). Здесь паразитное сопротивление, позволяющее учесть потери в реальном конденсаторе, показано штриховыми линиями.

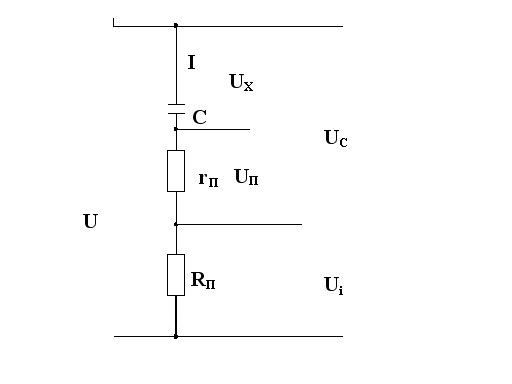
Рис. 7 – Последовательная схема замещения конденсатора

Пользуясь последней схемой цепи и найденными экспериментальными значениями , не представляет проблем построить векторную диаграмму токов и напряжений экспериментальной цепи. Эта диаграмма построена при дополнительном предложении что начальная фаза тока равна -90 . Поэтому под указанным углом вначале были отложены в некотором масштабе совпадающие по фазе комплексы

Затем построен с учетом найденного фазового сдвига комплекс . И, наконец, с учетом своего фазового сдвига, – вектор, соответствующий комплексу

Проекции из конца последнего вектора на вертикальную и горизонтальную оси определили размер векторов, соответствующих комплексам и -

После расчета по построенной диаграмме значений величин и подсчета и , может быть уточнено экспериментальное значение емкости конденсатора:

, (4.2)