История фракталов

Первым фракталом считается классическое множество Кантора или пыль Кантора, названное по имени Георга Кантора, который описал его в 1883 году. Существование пыли кантора отмечалось до этого Генри Смитом в 1875 году или ещё ранее. Это множество известно как пример множества нулевой меры Лебега, чья мощность равна мощности континуума c.

Построение классической пыли Кантора начинается с выбрасыванием средней трети (не включая концы) единичного отрезка. То есть исходное множество есть отрезок [0,1], и первый шаг состоит в удалении открытого интервала (1/3, 2/3). На следующем и всех остальных шагах выкидываем среднюю треть (не включая концы) всех отрезков текущего уровня. Таким образом, получается последовательность множеств рисунков:

Пеано нарисовал особый вид линии. Для ее рисования Пеано использовал следующий а лгоритм.

На первом шаге он брал прямую линию и заменял ее на 9 отрезков длинной в 3 раза меньшей, чем длинна исходной линии (Часть 1 и 2 рисунка 1). Далее он делал то же самое с каждым отрезком получившейся линии. И так до бесконечности. Ее уникальность в том, что она заполняет всю плоскость. Доказано, что для каждой точки на плоскости можно найти точку, принадлежащую линии Пеано. Кривая Пеано и пыль Кантора выходили за рамки обычных геометрических объектов. Они не имели четкой размерности. Пыль Кантора строилась вроде бы на основании одномерной прямой, но состояла из точек (размерность 0). А кривая Пеано строилась на основании одномерной линии, а в результате получалась плоскость. Во многих других областях науки появлялись задачи, решение которых приводило к странным результатам, на подобие описанных выше (Броуновское движение, цены на акции).

Вплоть до 20 века шло накопление данных о таких странных объектах, без какой либо попытки их систематизировать. Так было, пока за них не взялся Бенуа Р. Мандельброт (Benoit Mandelbrot), математик из Исследовательского центра им. Томаса Уотстона при IBM - отец современной фрактальной геометрии, который и предложил термин "фрактал" для описания объектов, структура которых повторяется при переходе к все более мелким масштабам. Работая в IBM математическим аналитиком, он изучал шумы в электронных схемах, которые невозможно было описать с помощью статистики. Постепенно сопоставив факты, он пришел к открытию нового направления в математике - фрактальной геометрии.

Что же такое фрактал. Сам Мандельброт вывел слово fractal от латинского слова fractus, что означает разбитый (поделенный на части). И одно из определений фрактала - это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого (по крайней мере, приблизительно).

Чтобы представить себе фрактал понаглядней рассмотрим пример, приведенный в книге Б. Мандельброта "The Fractal Geometry of Nature" ("Фрактальная геометрия природы") ставший классическим - "Какова длина берега Британии?". Ответ на этот вопрос не так прост, как кажется. Все зависит от длины инструмента, которым мы будем пользоваться. Померив берег с помощью километровой линейки мы получим какую-то длину. Однако мы пропустим много небольших заливчиков и полуостровков, которые по размеру намного меньше нашей линейки. Уменьшив размер линейки до, скажем, 1 метра - мы учтем эти детали ландшафта, и, соответственно длина берега станет больше. Пойдем дальше и измерим длину берега с помощью миллиметровой линейки, мы тут учтем детали, которые больше миллиметра, длина будет еще больше. В итоге ответ на такой, казалось бы, простой вопрос может поставить в тупик кого угодно - длина берега Британии бесконечна.

Типы фракталов.

Фракталы делятся на группы. Сейчас мы разберем самые большие из них:

• геометрические фракталы

• алгебраические фракталы

• системы итерируемых функций

• стохастические фракталы

Геометрические фракталы

Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений.

Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

Уже рассмотренная нами кривая Пеано является геометрическим фракталом. Классические примеры геометрических фракталов - Снежинка Коха, Лист, Треугольник Серпинского).

И з этих геометрических фракталов очень интересным и довольно знаменитым является первый - снежинка Коха. Строится она на основе равностороннего треугольника. Каждая линия которого ___ заменяется на 4 линии каждая длинной в 1/3 исходной _/\_. Таким образом, с каждой итерацией длинна кривой увеличивается на треть. И если мы сделаем бесконечное число итераций - получим фрактал - снежинку Коха бесконечной длинны. Получается, что наша бесконечная кривая покрывает ограниченную площадь. Для построения геометрических фракталов хорошо приспособлены так называемые L-Systems. Суть этих систем состоит в том, что имеется определенных набор символов системы, каждый из которых обозначает определенное действие и набор правил преобразования символов.

Например, описание снежинки Коха с помощью L-Systems в программе Fractint

; Adrian Mariano from The Fractal Geometry of Nature by Mandelbrot

Koch1 {

;устанавливаем угол поворота 360/6=60 градусов

Angle 6

; Начальный рисунок для построения

Axiom F--F--F

; Правило преобразования символов

F=F+F--F+F

}

В данном описании геометрические значения символов следующие:

F обозначает прочертить отрезок

+ поворот по часовой стрелке

- поворот против часовой стрелки

В торое свойство фракталов - самоподобие. Возьмем, например, треугольник Серпинского. Для его построения из центра треугольника мысленно вырежем кусок треугольной формы, который своими вершинами будет упираться в середины сторон исходного треугольника. Повторим эту же процедуру для трех образовавшихся треугольников (за исключением центрального) и так до бесконечности. Если мы теперь возьмем любой из образовавшихся треугольников и увеличим его - получим точную копию целого. В данном случае мы имеем дело с полным самоподобием.

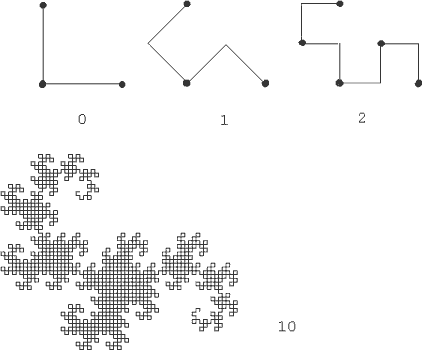
Драконова ломаная относится к классу самоподобных рекурсивно порождаемых геометрических структур. Ломаная нулевого порядка представляет собой просто прямой угол. Изображение фигуры каждого следующего порядка строится путем рекурсивных замен каждого из отрезков фигуры младшего порядка на два отрезка, сложенных также в виде прямого угла. При этом каждый первый угол оказывается "вывернутым" наружу, а каждый второй - вовнутрь. На рисунке проиллюстрирован алгоритм построения драконовой ломаной и изображен вполне взрослый "дракон" десятого порядка.