Форми запису злп. Основні означення

Загальний вигляд ЗЛП у розгорненій формі запису:

(min); (2.27)

(2.28)

(2.29)

ЗЛП, записана за допомогою знаків підсумовування, має вигляд

(min) (2.30)

(2.31)

(2.32)

Матрична форма запису ЗЛП. Позначимо:

- матрицю-рядок коефіцієнтів при змінних у цільовій функції розмірності ;

- матрицю-стовпець, невідомих розмірності ;

- матрицю системи основних обмежень розмірності ;

- матрицю-стовпець вільних членів розмірності .

Тоді ЗЛП (2.27) – (2.29) можна записати так:

(min); (2.33)

; (2.34)

(2.35)

Відомо, що на множині матриць відсутні відношення нерівності, тому (2.35) слід розуміти так, що всі елементи матриці Х є невід’ємними. Матриці, для яких виконується така умова, називаються напівдодатними.

Векторна форма запису ЗЛП. Позначимо:

- n-вимірнмй вектор, компонентами якого є коефіцієнти при змінних цільової функції;

- n-вимірний вектор змінних;

- m-вимірниі вектори, компонентами яких є коефіцієнти при змінних у системі основних обмежень;

- m-вимірний вектор, компонентами якого є вільні члени системи основних обмежень.

Тоді ЗЛП можна записати у вигляді

(min); (2.36)

(2.37)

(2.38)

Тут (2.38) позначає напівдодатність вектора , тобто те, що всі його компоненти невід’ємні.

Означення 2.6. Вектор , компонентами якого є коефіцієнти при змінній у системі основних обмежень ЗЛП, називається відповідним цій змінній.

Розглянемо приклад задачі використання ресурсів:

Z = 10x₁ + 11x₂ (max);

Зведемо її до стандартної форми канонічного вигляду:

(min) (2.39)

(2.40)

(2.41)

Випишемо відповідні вектори:

Система основних обмежень у векторній формі запису має вигляд

.

Підставивши компоненти відповідних векторів, можна показати, що ця векторна рівність еквівалентна системі (2.28).

Означення 2.7. ІІланом ЗЛП називається набір значень змінних , що задовольняє повну систему обмежень.

Означення 2.8. Розв’язком ЗЛП, або оптимальним планом, називається план, що забезпечує мінімум цільовій функції.

Повернемося до ЗЛП (2.39)-(2.41). Набір чисел Х₁=(5, 4, 8, 6, 1) не є планом цієї, ЗЛП, оскільки підстановкою його в (2.40) можна впевнитися, що він не задовольняє систему основних обмежень. Набір Х₂=(2, 4, -2, -6, -1) також не є планом, хоча він і задовольняє (2.40), але не задовольняє умову невід’ємності (2.41).

Набір Х₃=(2, 2, 14, 6, 1) є планом. Наведемо приклади ще кількох планів: Х₅=(0, 13/3, 16/3, 0, 8/3).

Випишемо значення цільової функції, що відповідають цим планам:

Виходячи з вигляду екстремуму, можна стверджувати, що план Х₃ кращий, ніж Х₄, а Х₅ , у свою чергу, кращий, ніж Х₃. У цьому разі відношення переваги полягає в наступному: чим менше значення , тим кращий відповідний план. Однак стверджувати, що Х₅ - оптимальний план, тобто розв'язок ЗЛП, не можна, оскільки порівнюють лише кілька планів і немає впевненості, що цей план - найкращий серед можливих.

Означення 2.9. План ЗЛП називається опорним, якщо його додатним компонентам відповідає система незалежних векторів.

Означення 2.10. Опорний план ЗЛП називається невиродженим, якщо

вектори, що відповідають його додатним компонентам, утворюють базис. У противному разі опорний план називається виродженим.

З’ясуємо, які з планів Х₃, Х₄ і Х₅ є опорним. План Х₃ має п’ять додатних компонент. Очевидно, він не може бути опорним, оскільки відповідні вектори тривимірні й у цьому просторі п’ять векторів завжди лінійно залежні.

Цей висновок правильний і в загальному випадку.

Теорема 2.3. Для того щоб план ЗЛП був опорним, потрібно, щоб його число додатних компонент не перевищувало розмірності векторного простору задачі, що визначається числом рівнянь у системі основних обмежень m.

Доведення. В m-вимірному векторному просторі максимальне число лінійно незалежних векторів дорівнює m, отже, число додатних компонент опорного плану не може перевищувати m, що й треба було довести.

Плани Х₄ і Х₅ містять по три додатні компоненти, а отже, можуть бути опорними. Вектори і , що відповідають додатним компонентам плану Х₄ , лінійно незалежні, оскільки вони є ортами і, більше того, утворюють ортонормований базис, тобто Х₄ – опорний не вироджений план.

План Х₅ також опорний не вироджений: вектори і , що відповідають його додатнім компонентам, лінійно незалежні. Дійсно, складемо їх лінійну комбінацію й прирівняємо її до нуль-вектора:

Дістанемо систему трьох лінійних рівнянь з трьома невідомими:

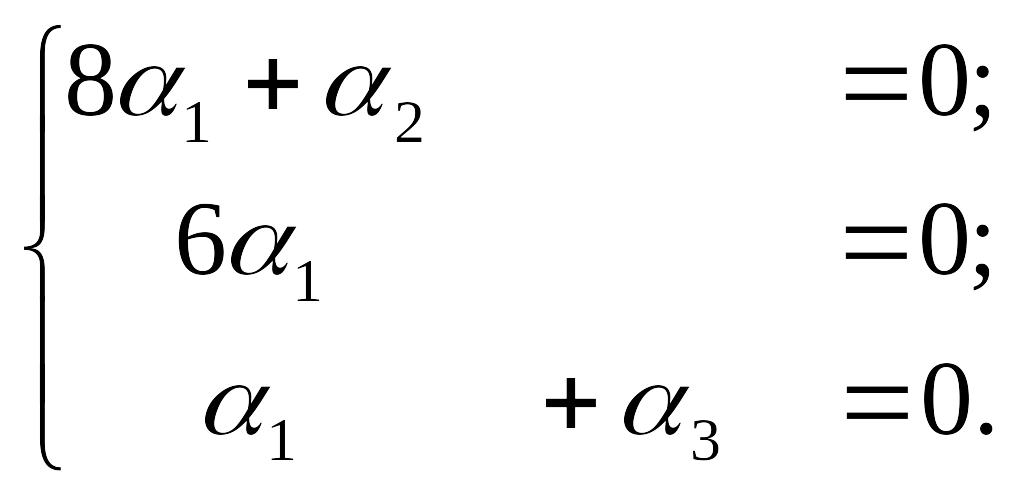
Помноживши друге рівняння на -8/6 і додавши його до першого, а потім – на -1/6 і додавши до третього, отримаємо

, тобто

Таким чином, і лінійно незалежні. Оскільки ці вектори з Е₃ і їх три, вони утворюють базис.

Деякі поняття теорії опуклих множин

Означення 1 Точка А називається опуклою лінійною комбінацією (ОЛК) точок якщо справедлива векторна рівность для якої виконуються умови

1. a₁+a₂…+…a_k = 1

2. a_i >=0

Означення 2 Множина G називається опуклою, якщо ОЛК будб-яких двох точок є точкою цією множини.

Геометрична інтерпритація. Баготокутник називається опуклим, якщо для будь-яких двох його точок, відрізок, який іх з’єднує належить багатокутнику.

Означення 3 Точка множини G називається кутовою точкою, якщо ії не можна представити у вигляді ОЛК двох відмінних точок цієї множини.

Означення 4 Точка множини G називається внутрішньою точкою, якщо можна указати такий окіл цієї точки, в якому знаходяться всі точки множини G.

Означення 5 Точка множини G називається граничною точкою, якщо в будь-якому околі цієї точки знаходяться як точки множини G, так і точки, які їй не належать.

Означення 6 Множина G називається замкнотою, якщо вона містить всі свої граничні точки.

Означення 7 Множина G називається обмеженою, якщо існує такий окіл, який містить всі точки множини G.

Означення опуклого многогранника. Опукла, замкнута, обмежини множина, яка вміщиє скінчене число кутових точок називається опуклим многогранником.

2.3 Властивості множини планів ЗЛП.

Основна теорема

Позначимо множину планів ЗЛП. Використовуючи матричну форму запису (2.31)-(2.33), можна записати

Теорема 2.4. Множина є опуклою.

Теорема 2.5. Множина К є замкненою. /Доведення теореми ґрунтується на матеріалі, що виходить за рамки цього курсу, тому теорему приймають без доведення./

Теорема 2.6. Опорному плану ЗЛП відповідає кутова точка множини К.

Теорема 2.7. Кутовій точці множини К відповідає опорний план.

Теореми 2.6 і 2.7 установлюють еквівалентність понять опорного плану та кутової точки множини К.

Теорема 2.8. Число кутових точок множини планів К скінчене.

Теорема 2.9. Якщо ЗЛП має розв’язок, тобто цільова функція досягає мінімуму на множині К , то такого самого значення вона набуває принаймні в одній із кутових точок.

Примітка. Якщо К – опукла многогранна область, то цільова функція необмежена на К зверху й знизу. В першому випадку розв’язок ЗЛП існує й твердження теореми 2.9 правильне, в другому – ЗЛП розв’язку не має.

Теорема 2.10 . Випадок неєдиності розв’язку ЗЛП. Якщо цільова функція досягає свого мінімального значення більш як в одній кутовій точці множини К, то ЗЛП має незлічену множину розв’язків, що є опуклою оболонкою цих кутових точок.