Прийняття рішень у полі шостої інформаційної ситуації

Нагадаємо, що ця ситуація характеризується наявністю чин­ників, які зумовлюють «проміжну» між п'ятьма розглянутими вище інформаційними ситуаціями поведінку економічного се­редовища щодо вибору своїх станів.

Класичними прикладами критеріїв прийняття компромісних рішень у полі шостої інформаційної ситуації є критерій Гурвіца, модифіковані критерії та критерій Ходжеса-Лемана.

1) Критерій Гурвіца. Гурвіц запропонував використовувати зважену комбінацію найкращого та найгіршого. Такий підхід до вибору рішень відомий як критерій показника песимізму-оптимізму. Особливістю цього критерію є те, що в ньому передбачається не повний, а частковий антагонізм середовищ та СПР.

Згідно з критерієм Гурвіца, у випадку, коли F = F⁺, оптималь­ним є рішення:

Величину називають

-показником Гурвіца для рішення .

У випадку, коли , оптимальним є рішення:

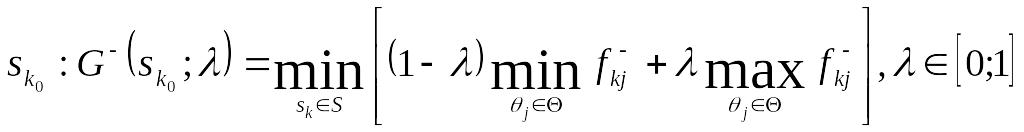
Параметр , в обох випадках можна інтерпретувати як коефіцієнт несхильності до ризику.

2) Модифіковані критерії. Згідно з модифікованими критерія­ми, у випадку, коли F = F⁺, оптимальним є рішення:

або у випадку, коли , рішення:

де а як величи­ну можна використати середньоквадратичне семіквадратичне відхилення тощо. Пара­метр , який використовують у зазначених вище критеріях, можна тлумачити як коефіцієнт несхильності СПР до ризику.

3) Критерій Ходжеса-Лемана. Ходжес та Леман стоять на тій позиції, що в практиці прийняття рішень за умов невизначе­ності інформація про стан ЕС перебуває між повним незнанням та точним знанням апріорного розподілу. Критерій Ходжеса-Лемана дає змогу використовувати всю інформацію, яку має суб'єкт управління, і водночас забезпечує заданий рівень гаран­тії у випадку, коли ця інформація неточна. У певному плані критерій Ходжеса-Лемана являє собою «суміш» критеріїв Байєса та Вальда.

Згідно з критерієм Ходжеса-Лемана, у випадку, коли F = F⁺, оптимальним є рішення:

.

Якщо то оптимальним рішенням є:

.

Як і раніше, параметр , і його можна інтерпретувати як коефіцієнт несхильності до ризику.

Прийняття рішень, оптимальних за Парето

Необхідно зазначити, що, згідно з Парето, рішення Sk вважа­ється не гіршим від рішення (позначається: ), якщо для всіх елементів відповідних їм векторів мають місце оцінки , якщо F = F⁺або , якщо .

Якщо хоча б для однієї компоненти вектора має місце строга нерівність чи , то рішення вважається кращим за рішення (записується )

Рішення є оптимальним за Парето, якщо в множині S не знайдеться рішення, кращого за .

Необхідно звернути увагу на те, що на практиці ситуація, коли рішення, що приймається, буде оптимальним за Парето, трапля­ється нечасто. А тому за відсутності рішення, оптимального за Парето, створюють множину непокращуваних за Парето рішень . (Нагадаємо, що рішення називають покращува­ним, якщо існує таке рішення , що Тоді оптималь­не рішення доцільно шукати серед елементів множини Парето , використовуючи при цьому критерії, адекватні ситуації при­йняття рішень.

Задача.

Фірма ставить за мету вихід на міжнародний ринок зі своєю продукцією. ЇЇ фахівцями опрацьовано чотири варіанти рішень х1,х2,х3,х4 щодо випуску продукції. Маркетингові дослідження й опрацювання набутої інформації показати, що рішення залежать від попиту (стану економічного середовища), який можна представити трьома варіантами Q1,Q2,Q3. На базі застосування відповідних економіко-математичних (імітаційних) моделей розрахованого функціонал оцінювання (прибуток у тис. грн.) який наведено в таблиці.

Варіанти рішень	Варіанти станів середовищ
	Q1	Q2	Q3
X1	2.0	3.0	1.5
X2	7.5	2.0	3.5
X3	2.5	8.0	2.5
X4	8.0	5.0	4.5

Відомо також, що стан середовища Q1 може реалізуватися з імовірністю р1=0,1; Q2-0,5; Q3-0,4. З іншого боку фірма впевнена, що зіштовхнеться з конкурентами. Керівництво фірми вважає, що враховувати вплив конкуренції необхідно з вагою .

Необхідно обрати один із чотирьох варіантів рішення, який буде оптимальним:

а) згідно з критерієм Ваьда;

б) згідно з критерієм Севіджа;

в) згідно з критерієм Байєса;

г) згідно з критерієм Ходжена-Лемена.

Побудувати множину і ламану Ходжена-Лемана.

Розв’язання: