4.1.3. Аналітичні методи згладжування динамічних рядів

Аналітичні методи згладжування часових рядів ґрунтуються на припущенні, що відомий загальний вигляд невипадкової складової часового ряду, і реалізуються за допомогою регресивних та адаптивних моделей. Найбільш простим із методів прогнозування являється метод екстраполяції тренду динамічного ряду, обчисленого за попередній період. Розглянемо метод екстраполяції на основі кривих зростання. Для макроекономічних процесів використовуються певні види кривих зростання. Для того, щоб найкращим способом підібрати криву для моделювання і прогнозування економічного явища, необхідно знати особливості кожного виду кривих. Важливе значення має знаходження довірчого інтервалу прог­нозу, тобто розрахунок інтервалу, до якого з певною імовірністю належить прогнозна величина.

Розглянемо деякі моделі тренду і дамо їм характеристику в змістовних термінах показників розвитку динаміки часового ряду.

Криві, які найчастіше використовуються в макроекономічних дослідженнях, їх рівняння та формули перетворення функцій до лінійного виду зведемо до таблиці.

Таблиця 4.9

Основні види кривих	Форми кривої	Перетворення функції до лінійного виду
1	2	3
Лінійна (поліном першого ступеня)		Не потрібні
Квадратична (поліном другого ступеня)
Поліном третього ступеня
Експоненційна (проста)
Логарифмічна крива		,
S-подібна крива
1	2	3
Обернено-лога­риф­мічна крива		, ,
Степенева
Гіперболічна крива І типу		,
Гіперболічна крива ІІ типу		,
Гіперболічна крива ІІІ типу		, , , ,
Модифікована експонента		; ;
Крива Гомперця
Логістична крива		,

Завдання полягає в тому, щоб з’ясувати, який саме із трендів вибрати в залежності від показників динаміки часового ряду: абсолютного ланцюгового приросту, ланцюгового темпу приросту та прискорення.

1. Лінійна функція . В цій моделі – теоретичний рівень базисного року, – абсолютний ланцюговий приріст . Тобто, якщо для динамічного ряду абсолютний ланцюговий приріст є майже сталою величиною, то такий ряд можливо вирівняти по прямій лінії. Зауважимо, що в цьому випадку, ланцюговий темп приросту монотонно спадає та прямує до 0 при .

2. Показникова функція або .

Якщо для динамічного ряду абсолютний приріст збільшується, а ланцюговий темп приросту сталий, то динамічний ряд можливо вирівняти по експоненті . Дійсно, якщо , то , або .

Зауважимо, що в першій із приведених функцій – теоретичний початковий (базисний) рівень, а – дискретний темп приросту.

Маємо

,

або .

Для експоненти , – неперервний темп приросту .

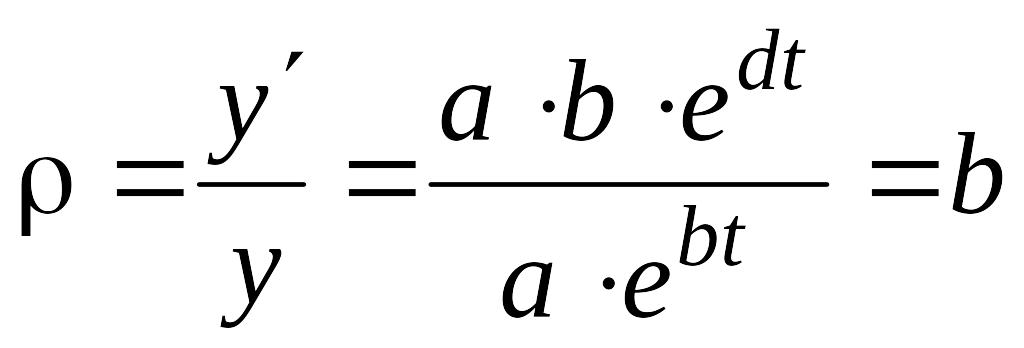3. Квадратний тричлен , .

Тоді динамічний ряд можна вирівняти по параболі в тому випадку, коли абсолютний ланцюговий приріст збільшується, абсолютний ланцюговий темп приросту зменшується, а прискорення є сталою величиною. Цей висновок випливає із формул:

; ; .

4. Гіперболічна крива , . За допомогою цієї кривої можна вирівняти ряди динаміки зі спадаючим ланцюговим приростом .

Зауважимо, що при , тобто крива обмежена зверху прямою .

Особливості застосування інших кривих зростання для згладжування часових рядів були розглянуті в розділі 4.4.

Розглянемо приклад.

В таблиці приведено згладжений за допомогою методу ковзної середньої динамічний ряд кількості реалізованих нафтопродуктів протягом 13 років.

Таблиця 4.10

Рік	1988	1989	1990	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000
Кількість нафтопрод. (т.тон)	127	132	150	172	174	175	180	183	193	209	235	236	254

Показники динамічного ряду зведемо до таблиці.

Таблиця 4.11

Рік	Рів­ні	Базовий приріст	Ланцю-говий приріст	Базисний темп росту	Ланцю-говий темп росту	Базисний темп приросту	Ланцю-говий темп приросту	При­ско­рення
1988	127	–	–	–	–	–	–	–
1989	132	5	5	1,04	1,04	0,04	0,04	–
1990	150	23	18	1,18	1,14	0,18	0,17	13
1991	172	45	22	1,35	1,15	0,35	0,3	4
1992	174	47	2	1,37	1,01	0,37	0,27	-20
1993	175	48	1	1,38	1,01	0,38	0,28	-1
1994	180	53	5	1,42	1,03	0,42	0,3	4
1995	183	56	3	1,44	1,02	0,44	0,3	-2
1996	193	66	10	1,52	1,07	0,52	0,36	7
1997	209	82	16	1,65	1,08	0,65	0,42	6
1998	235	108	24	1,85	1,12	0,85	0,52	8
1999	236	109	1	1,86	1,004	0,86	0,46	-23
2000	254	127	18	2,00	1,08	1,00	0,54	17

Вивчаючи показники, одержані в попередній таблиці, впевнюємося в тому, що ланцюговий темп приросту майже однаковий для всіх років (включаючи 1989 рік), а абсолютний ланцюговий приріст в основному зростає. Таким чином, в якості тренду можна вибрати експоненту , яка лінеаризується шляхом логарифмування. Маємо

;

якщо позначити , , , то отримаємо лінійне рівняння регресії: .

Для знаходження оцінок параметрів лінійного рівняння регресії і для з’ясування питання адекватності моделі, розв’язування проблеми тісноти зв’язку та прогнозування побудуємо таблицю.

Таблиця 4.12

1	2	3	4	5	6	7	8
1	4,8442	1	4,8442	4,8863	0,1308	0,1021	0,0018
2	4,8828	4	4,9396	4,9396	0,1044	0,0709	0,0032
3	5,0106	9	5,0318	4,9929	0,0381	0,0454	0,0003
4	5,1475	16	20,59	5,0462	0,0034	0,0255	0,0103
5	5,1591	25	25,7955	5,0995	0,0022	0,0113	0,0036
6	6,1648	36	30,9888	5,1528	0,0017	0,0028	0,0001
7	5,1930	49	36,351	5,2061	0,0002	0,0000	0,0002
8	5,2095	64	41,676	5,2594	0,0000	0,0029	0,525
9	5,2627	81	47,3643	5,3127	0,0032	0,0114	0,0025
10	5,3423	100	53,423	5,3660	0,0186	0,0256	0,0006
11	5,4596	121	60,0556	5,4193	0,0644	0,0455	0,0016
12	5,4638	144	65,5656	5,4726	0,0655	0,0697	0,0001
13	5,5373	169	71,9849	5,5259	0,1098	0,01024	0,0001
å	67,6772	819	483,4363		0,5433	0,5128	0,0269

Складемо нормальну систему рівнянь для визначення оцінок параметрів і , яка має вигляд:

.

Розв’язок системи отримаємо за правилом Крамера:

,

,

.

Тобто , .

Таким чином, побудована лінійна модель для емпіричних даних, приведених в таблиці: , а експонента має вид: .

Для перевірки адекватності лінійної моделі нам необхідні знання сум, які знаходяться в стовпцях (5, 6, 7, 8) таблиці.

Зробимо необхідні обчислення :

; ;

; ;

; ;

; ;

; ;

; ;

.

Користуючись формулою , отримаємо значення .

Адекватність моделі перевіримо, використовуючи критерій Фішера.

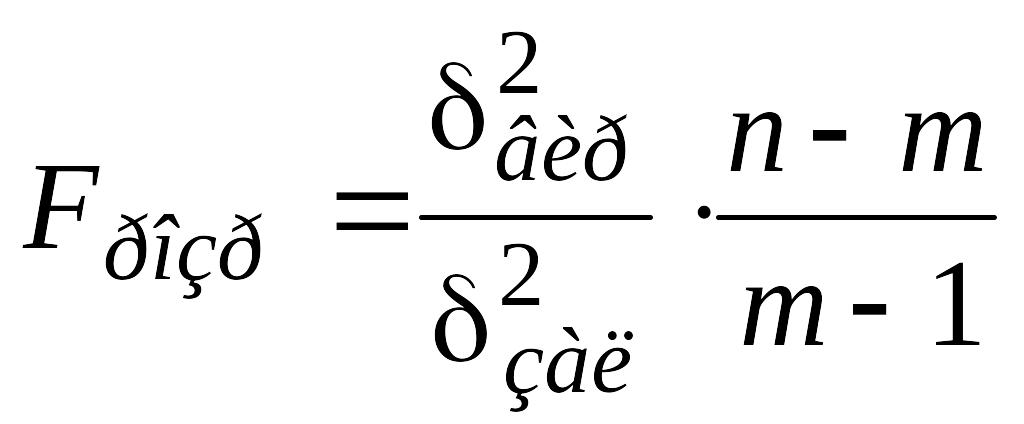, тобто ,

.

Оскільки , то побудована модель адекватна згладженому динамічному ряду.

Коефіцієнт кореляції лінійної моделі обчислимо за формулою

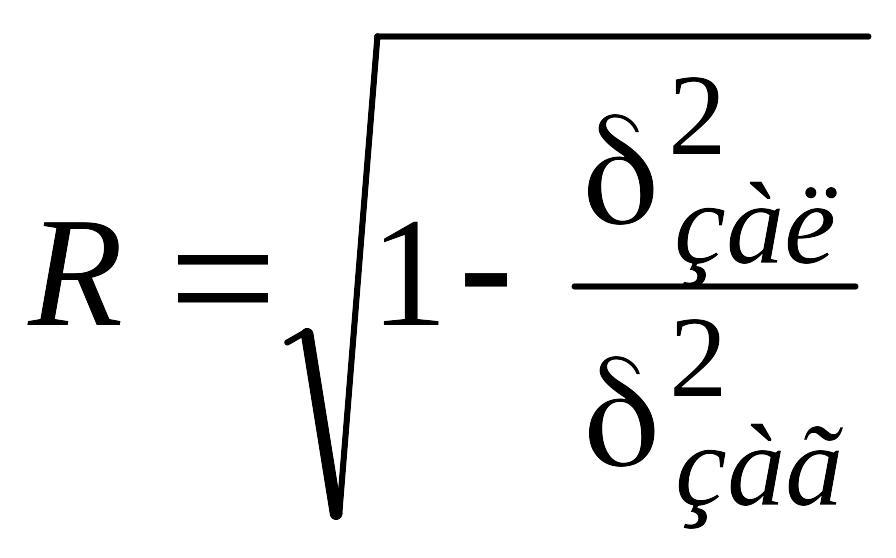, тобто .

Оскільки значення близьке до одиниці, то це свідчить про дуже тісну залежність кількості реалізованих нафтопродуктів від часу.

Приклад

Для знаходження точкового прогнозу реалізації нафтопродуктів на 2001 та 2002 роки в лінійне рівняння регресії або експоненту підставляємо замість значення та , отримаємо , звідки .

Майже таке ж значення маємо, якщо підставити в рівняння експоненти: .

Аналогічно,

, .

Для знаходження інтервального прогнозу скористаємося подвійною нерівністю , де обчислюється за формулою:

.

В даному випадку:

, ; ; .

Знайдемо та для і відповідно одержимо:

,

.

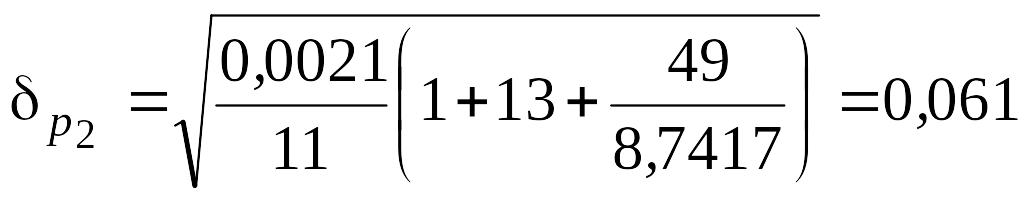Визначимо тепер прогнозні інтервали для лінійної та експоненційної моделей.

Одержимо для лінійної моделі:

, або .

Для експоненційної моделі .

Аналогічні розрахунки отримаємо при для лінійної та експоненційної моделей відповідно:

, або ; .

Таким чином, з імовірністю 0,95 можна стверджувати, що прогнозні значення та належать відповідно інтервалам та .