4.1.2. Методи згладжування часових рядів

Методи згладжування часових рядів поділяються на дві групи:

• механічне згладжування окремих рівнів часового ряду, яке не потребує знань про аналітичний вид функції, що згладжує часовий ряд;

• аналітичне згладжування, з використанням певної кривої, яка відображає тенденцію, притаманну ряду.

Розглянемо два методи механічного згладжування:

1. метод простої ковзної середньої;

2. метод простого експоненційного згладжування.

При використанні першого методу головне припущення полягає в тому, що часовий ряд будується за формулою y_t = bt+ , де - невідомий параметр, який знаходиться на базі вхідної інформації, – випадкова помилка, середнє значення якої , а – стала величина.

Крім того припускаємо, що дані для різних періодів часу не корельовані, тобто коваріація і дорівнює нулю.

Метод простої ковзної середньої припускає, що всі спостережень застосовуються з однаковою вагою для оцінки параметра . Тобто, якщо в заданий момент часу останні рівнів є , , ..., , то

,

де – оцінюване значення для моменту часу . Відсутній чіткий метод для визначення числа – бази методу, який використовує ковзну середню. Якщо є підстави вважати, що спостереження довготривалі і узгоджені з моделлю y_t = bt+ , то варто вибирати великі значення . Якщо ж дані спостережень задовольняють заданій моделі на протязі коротких проміжків часу, то можна брати малим. На практиці змінюється від 2 до 10.

Недоліком методу є його застосування лише для рядів, які мають лінійну тенденцію.

Як приклад розглянемо динамічний ряд реалізації нафтопродуктів протягом 15 років однією із компаній, зведений до таблиці (табл. 4.4).

Таблиця 4.4

T	1986	1987	1988	1989	1990	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000
V	170	120	105	156	189	170	167	205	178	156	189	235	203	267	239

де Т – роки, V – об’єм реалізації в млн. тон.

В системі координат на площині побудуємо точки з координатами , а потім з’єднаємо їх відрізками прямих і одержимо емпіричну лінію регресії (рис. 4.1).

Рис. 4.1

Спостерігаючи одержану лінію, ми бачимо, що протягом часу кількість реалізованих нафтопродуктів має тенденцію зростання. Однак, лінія має зигзагоподібний характер, що пояснюється чинниками, які не завдають постійного впливу на обсяг реалізації нафтопродуктів. Цей вплив пояснюється довгостроковими (циклічними) та випадковими коливаннями. Якщо розглянути реалізацію нафтопродуктів на протязі декількох років по місяцям, то впевнимось в тому, що відповідна ломана буде мати ще більш зигзагоподібний характер. Це пов’язано з тим, що, наприклад, в зимові місяці кількість нафтопродуктів буде більшою, ніж в середньому за рік (в зв’язку з опалювальним сезоном). Наступний пік спостерігається в квітні-травні (посівна компанія), в липні-серпні (жнива).

Тобто, вид емпіричної лінії залежить від різних факторів. Нас цікавить вивчення залежності обсягу реалізації від фактору часу в цілому, а саме, по якій лінії можна вирівняти задану емпіричну лінію. Для розв’язування цього питання нам треба зневілювати (провести згладжування) впливу інших факторів. Для цього використаємо метод ковзної середньої, тобто, для кожного значення регресанту , починаючи з другого і закінчуючи передостаннім, розглянемо середнє значення , тобто .

Наприклад, (в середньому це відповідає 1987 року).

Щоб не втратити перший і останній рівні, їх згладжують за формулами:

; ;

(для 1988 року).

В нашому випадку:

;

Результати обчислень зведемо до таблиці 4.5.

Таблиця 4.5

1986	170	164,1667
1987	120	131,6667
1988	105	127
1989	156	150
1990	189	171,6667
1991	170	175,333
1992	167	180,6667
1993	205	183,333
1994	178	179,6667
1995	156	174,3333
1996	189	193,3333
1997	235	209
1998	203	235
1999	267	263,3333
2000	239	254,3333

За одержаними даними побудуємо нову лінію регресії (рис. 4.2).

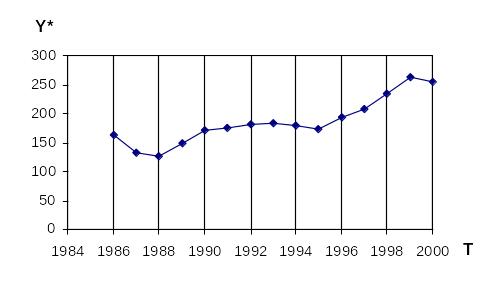
Рис. 4.2

З графіку випливає, що вона має більш згладжений вигляд в порівнянні з попередньою. Ще більш згладжений вигляд буде мати лінія, якщо для обчислення ковзної середньої будемо брати не три значення ( ) регресанту, а чотири, п’ять і так далі.

Але неважко помітити, що при збільшені , тобто при збільшені числа доданків в чисельнику ковзної середньої, кількість експериментальних точок буде зменшуватись. Тому ми повинні вибрати таку кількість доданків (тобто базу ), щоб отримана емпірична лінія мала гладкий вигляд, а з іншого боку, щоб кількість емпіричних точок була достатньою для побудови емпіричної лінії регресії. Після згладжування лінії регресії можна вибрати тренд і знайти параметри його рівняння. В подальшому для побудови теоретичної моделі тренду використовують вже згладжений динамічний ряд, тобто дані, зведені до таблиці 4.6.

Таблиця 4.6

1986	164,1667
1987	131,6667
1988	127
1989	150
1990	171,6667
1991	175,333
1992	180,6667
1993	183,333
1994	179,6667
1995	174,3333
1996	193,3333
1997	209
1998	235
1999	263,3333
2000	254,3333

В системі нормальних рівнянь замість значень будемо використовувати значення ковзних середніх . Слід зауважити, що використання незгладженого ряду може привести до неадекватного вибору тренду. Якщо ж довгострокові (циклічні), сезонні, випадкові коливання незначні, то використання методу ковзної середньої недоцільно.

Розглянемо ще метод простого експоненційного згладжування. Ідея методу полягає в тому, щоб усунути недоліки методу ковзної середньої, пов’язані з тим, що всі дані при визначенні середньої мають однакову вагу.

Метод експоненційного згладжування надає найбільшу вагу останньому спостереженню, а вага попередніх спадає геометрично.

Визначимо величину , як постійну згладжування ( ). Якщо відомі рівні часового ряду для минулих моментів , то оцінка для моменту часу обчислюється за формулою:

.

Коефіцієнти при , , і так далі поступово зменшуються, тобто ця процедура надає більшу вагу останнім (за часом) спостереженням.

Формулу для обчислення можна привести до слідуючого більш простого вигляду:

, , при цьому .

Таким чином, значення можна обчислити, користуючись отриманою рекурентною формулою. Із рекурентної формули випливає, що .

Вибір постійної згладжування є основним вирішальним моментом при обчисленні значень прогнозної величини.

Велике значення приписує більшу вагу останнім спостереженням. На практиці постійна згладжування приймає значення на сегменті , тобто .

Як приклад, розглянемо динамічний ряд числа проданих кондиціонерів за 24 місяці (табл. 4.7).

Таблиця 4.7

1	22	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
46	56	54	43	57	56	67	62	50	56	47	56	54	42	64	60	70	66	57	55	53	62	70	72

Виберемо . Отримані значення зведемо до таблиці 4.8.

Таблиця 4.8

1	46	–
2	56	46
3	54
4	43
5	57
6	56
7	67
8	62
9	50
10	56
11	47
12	56
13	54
14	42
15	64
16	60
17	70
18	66
19	57
20	55
21	52
22	62
23	70
24	72
25

Універсальним же методом попереднього вибору кривих зростання є метод середніх та граничних характеристик приросту. Він застосований на використанні окремих характеристик властивостей кривих, які були розглянуті вище.

При цьому методі вхідний часовий ряд попередньо згладжується методом простої ковзної середньої. Наприклад, для інтервалу згладжування згладжені рівні розраховуються за формулою . Щоб не втратити перший і останній рівні їх згладжують за формулами:

; .

Далі розраховуються перші середні прирости , ; другі середні прирости , а також ряд похідних величин: ; ; ; .

Якщо перший середній приріст майже однаковий, то вибирається поліном першого порядку (пряма).

Якщо перший середній приріст змінюється лінійно, то вибирається поліном другого порядку (парабола).

Поліном третього порядку вибирають, якщо другий середній приріст змінюється лінійно. Просту експоненту вибирають в випадку, якщо величина майже однакова, модифіковану експоненту – якщо величина змінюється лінійно.

Крива Гомперця та логістична крива використовуються, наприклад, в демографії.

Експоненційно можна згладжувати не тільки сам ряд, а і коефіцієнти тренду, лінійного або ж експоненційного, коефіцієнти сезонності, тощо.

Параметр згладжування в моделі також може бути не постійною, а змінною величиною.

Відповідні методи називаються методами адаптивного згладжування.