Поняття задачі квадратичного програмування

Задача квадратичного програмування – окремий випадок задачі нелінійного програмування, коли повна система обмежень така сама, як і в задачі лінійного програмування, а цільова функція є квадратичною формою. Отже, задача квадратичного програмування має вигляд

(2.136)

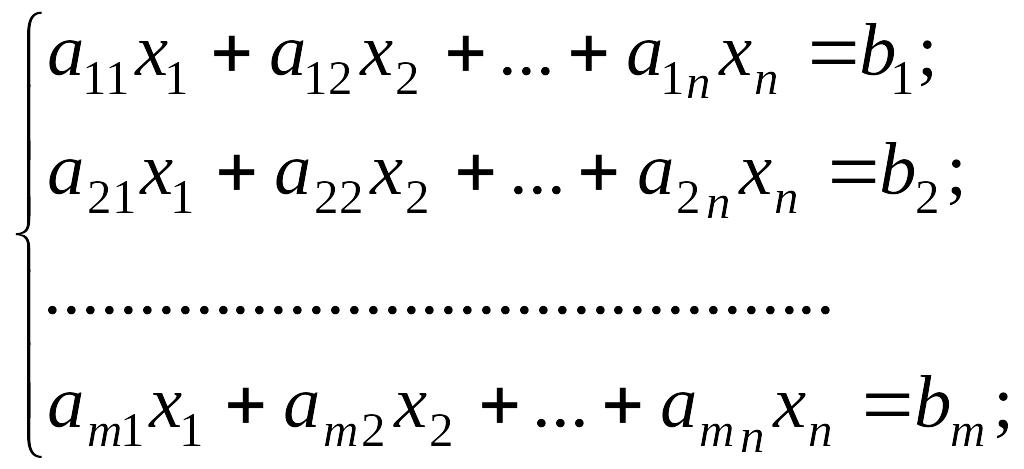(2.137)

. (2.138)

Запишемо задачу в матричній формі. Введемо матриці:

С = (с₁, с₂, ..., с_n); ; ; X^T = (x₁, x₂, ..., x_n);

A = ||a_ij||; D = ||d_ij||.

При цьому припускається, що матриця D симетрична, тобто d_ij = d_ji.

Задача квадратичного програмування в матричній формі мав вигляд

Z = СХ + X^ТDX (min); (2.139)

AХ = B; (2.140)

Х ³ B. (2.141)

Як і в загальному випадку для задач нелінійного програмування, не існує ефективного обчислювального методу і для обчислення глобального екстремуму задачі квадратичного програмування, якщо лише наперед не відомо, що будь-який локальний екстремум є одночасно глобальним. Оскільки в задачі (2.139)-(2.141) множина планів опукла, то будь-який локальний мінімум (максимум) є глобальним, якщо цільова функція опукла.

Цільова функція є сумою лінійної функції СХ (яка є і опуклою, й угнутою) та функції X^ТDX, що є квадратичною формою.

Розглянемо деякі властивості квадратичних форм.

Означення 2.21 Вираз вигляду називається квадратичною формою. Очевидно, що квадратичну форму можна записати в матричному вигляді:

Q(Х) = X^ТDX.

Якщо Q(X) > 0 (Q(X) < 0) для всіх Х ¹ 0, то квадратична форма Q(X) називається додатно (від’ємно) визначеною.

Якщо Q(X) ³ 0 (Q(X) £ 0) для всіх Х ¹ 0, то квадратична форма Q(X) називається невід’ємно (недодатно) визначеною.

Якщо для одних Х Q(X) > 0, а для інших Q(X) < 0, то квадратична форма Q(X) називається невизначеною.

Припустимо, що матриця D симетрична. Дійсно, значення Q(X) не зміняться, якщо кожний із пари коефіцієнтів d_ij і d_ji (і¹ j) замінити на .

Приклад. Розглянемо квадратичну форму Q(X), породжену матрицею

і квадратичну форму Q*(X), породжену матрицею D*:

Отже, Q(X) º Q*(X) – це та сама квадратична форма. Однак D ¹ D*, причому матриця D* симетрична і її отримано з D: елементи (і ¹ j) дорівнюють півсумі відповідних елементів матриці D.

Із вищої математики відомо, що квадратичну форму за допомогою лінійного перетворення можна перетворити до канонічного вигляду, тобто до вигляду, який містить лише квадрати змінних:

Q(X) = .

У результаті такого перетворення визначається вигляд форми:

1) якщо всі a_і > 0, то квадратична форма додатно визначена;

2) якщо всі a_і < 0 – від’ємно визначена;

3) якщо a_і мають різні знаки – невизначена.

Справедлива наступна теорема про ознаки, що дає можливість, не зводячи квадратичну форму до канонічного вигляду, встановити вигляд визначеності або невизначеності квадратичної форми.

Теорема 2.24 Якщо для квадратичної форми Q(Х) = X^ТDX усі визначники D₁, D₂, ..., D_п відмінні від нуля, то цю форму можна перетворити до канонічного вигляду і (і = ), де

.

Із цієї теореми випливає:

1) якщо всі визначники D₁, D₂, ..., D_п додатні, то всі a_і > 0 і квадратичне форма додатно визначена;

2) якщо в ряду 1, D₁, D₂, ..., D_п знаки чергуються, то всі a_і < 0 і квадратична форма від’ємно визначена;

3) якщо ранг матриці D(r) менше від п (r > n) і перші r її визначників додатні, то квадратичне форма невід’ємно визначена;

4) якщо r < n і в ряду 1, D₁, D₂, ..., D_r знаки чергуються, то квадратична форма недодатно визначена;

5) якщо r < n і в ряду 1, D₁, D₂, ..., D_r немає чергування знаків, то відповідно квадратична форма невизначена.

Приклад. Визначити вигляд квадратичної форми

Q(x₁, x₂, x₃) = .

Розв’язання. Складемо матрицю D:

;

;

.

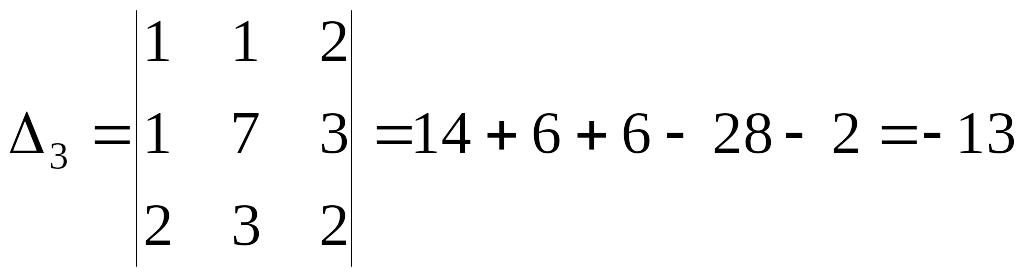Оскільки дістали ряд 1, 1, 6, –13, маємо 5-й випадок, тобто квадратична форма невизначена.

Із вищої математики відомо, що коли квадратична форма додатно чи від’ємно визначена, то X^ТDX – опукла функція.

Розв’язок задачі квадратичного програмування шукатимемо в припущенні, що функція X^ТDX, а отже, й цільова функція є опуклими.

Скористаємося умовами Куна-Таккера (2.134)-(1.137), щоб отримати необхідні та достатні умови оптимальності плану задачі (2.139)-(2.141).

Складемо функцію Лагранжа:

або в матричній формі

, (2.142)

це L = (l₁, l₂, ..., l_m).

Випишемо частинні похідні:

,

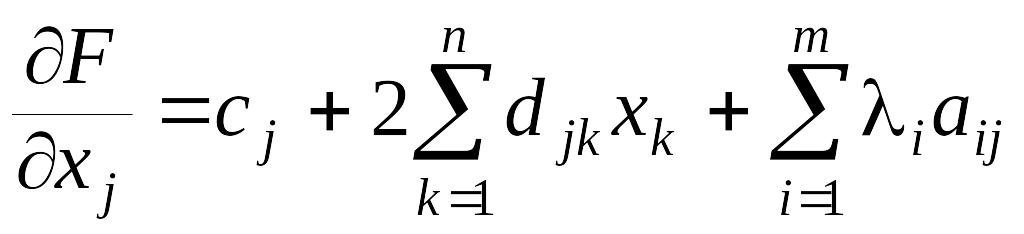або в матричній фopмi

.

Аналогічно

.

Якщо Х* – оптимальний план задачі квадратичного програмування, то має існувати така матриця L*, що (X*, L*) задовольняє умову (2.134), тобто умову = 0. У цьому разі умови (2.135) мають вигляд А×Х* = В. Оскільки обмеження в задачі подано у вигляді рівнянь, то на l_і (і =  ) не накладаються умови невід’ємності, умови (2.134) виконуються для будь-якого плану, отже, їх можна виключити. Таким чином, якщо існують Х* ³ 0, L*, які задовольняють умови

А×Х* = В;

; (2.143)

,

то X* є оптимальним планом задачі квадратичного програмування (2.139)-(2.141).