Класичні методи оптимізації

У попередніх розділах досить повно викладено лінійне програмування. Крім того, розглянуто задачу математичного програмування, в якій система основних обмежень і цільова функція лінійні, однак спеціальні обмеження включають цілочисловість змінних (ЗЦЛП). Ця задача належить до класу задач нелінійного програмування.

У цьому розділі розглядаються деякі методи розв’язування задач із нелінійними цільовою функцією або системою обмежень.

Методи розв'язування нелінійних задач використовують алгоритми, аналогічні алгоритму симплексного методу. Однак ці алгоритми не є універсальними, тому методи їх розв'язування розроблено лише для кількох типів задач.

Графічна інтерпретація особливостей розв’язування задач нелінійного програмування

Розглянемо деякі властивості нелінійних функцій, що роблять задачі нелінійного програмування важчими порівняно з лінійними.

Відомо, що для задач лінійного програмування виконуються такі властивості.

1. Множина планів опукла, замкнена й містить скінченне число кутових точок.

2. Множина точок т-вимірного простору, в яких цільова функція набуває заданого значення, є гіперплощина. Крім того, гіперплощини, що відповідають різним значенням цільової функції, паралельні.

3. Якщо цільова функція обмежена знизу, то оптимальним розв'язком є принаймні одна з кутових точок.

4. Локальний мінімум є також глобальним мінімумом, тобто не існує локального оптимуму цільової функції, відмінного від глобального оптимуму.

Більша частина цих властивостей у задачах нелінійного програмування не виконується.

Розглянемо поняття локального та глобального оптимумів на прикладі функції однієї змінної. На рис. 2.12 показано максимуми й мінімуми функції f(x) на відрізку [а, b].

Точки х₁, х₂, х₃, х₄, х₅, х₆ визначають екстремуми функції f(x), причому х₁, х₃, х₆ – максимуми, а х₂ і х₄ – мінімуми. Оскільки f(x₆) = max{f(a), f(x₁), f(x₃), f(x₆), f(x_b)}, то f(x₆) – глобальний максимум, аналогічно f(x₂) – глобальний мінімум. Для зведеної функції існують локальні екстремуми, відмінні від глобального екстремуму f(x₄) від f(x₂), f(x₁) і f(x₃) від f(x₆).

Рис. 2.12

Максимум у точці х₁ відрізняється від решти максимумів. Це точка і нестрогого максимуму на відміну, наприклад, від точки x₃, яка визначає строгий максимум.

Означення 2.17 Точка x₀ є точкою нестрогого максимуму, якщо знайдеться такий e-окіл цієї точки, в якому f(x₀) ³ f(x), " х Î u_e(х₀), x ≠ х₀, і точкою строгого мінімуму, якщо f(x₀) > f(x), " x Î u_e(x₀), x ≠ х₀. На рис. 2.12 можна виділити ще одну характерну точку х₅. У цій точці перша похідна, так само як і в точках х₁, х₂, х₃, х₄, дорівнює нулю (дотична до графіка функції в цій точці паралельна осі ОХ), однак це не точка екстремуму. Такі точки називають точками перегину.

Для довільної задачі нелінійного програмування деякі або всі з указаних властивостей 1-4 не виконуються. Проілюструємо це на конкретних прикладах.

Приклад 1.

х₁ ³ 0, х₂ ³ 0.

Розв’язання. Множина планів задачі утворює многокутник ABCD (рис. 2.13). Лінією рівня цільової функції є коло (x₁ – 7)² + (x₂ – 8)² = C з центром (7; 8). Із зменшенням С (квадрат радіуса) значення цільової функції зменшується. Очевидно, що цільова (функція набуває мінімального значення в точці М (тут лінія рівня дотикається до многокутника АВСD), що не є кутовою. Обчислимо координати цієї точки. Для цього складемо рівняння прямої МР, МР^ВС, отже, рівняння МР має вигляд (x₂ – 8) = R(х₁ – 7), де R = (умова перпендикулярності). Після перетворень маємо 4х₁ – 3х₂ – 4 = 0. Щоб визначити координати точки М, розв'яжемо систему

Рис. 2.13

Ї ї розв’язок

.

Оптимальний план: = 88/25; = 84/25, при цьому Z_min ⁼ = 841/25.

Приклад 2. Повна система обмежень така сама, як і в прикладі 1, a Z = (x₁ – 3)² + (х₂ – 3)². Знайти плани, що надають найменшого та найбільшого значень цільовій функції.

Розв’язання. Мінімального значення цільова функція набуває в точці Р(3; 3) (рис. 2.14): Z_min = 0. Цільова функція має два локальних максимуми: в кутовій точці В(0; 6) Z(В) = 18 і в кутовій точці С(8; 0) Z(С). = 34. Найбільше значення досягається в кутовій точці С(8; 0). Оптимальні плани: =3; = 3 – йому відповідає Z_min = 0 і = 8, – йому відповідає Z_mах = 34.

У наведених прикладах 1 і 2 (на мінімум цільової функції) локальний оптимум збігається з глобальним, однак досягається не в кутовій точці, а на межі області (приклад 1) або у внутрішній точці (приклад 2). З іншого боку, в прикладі 2 (на максимум цільової функції) глобальний оптимум досягається в точці С і існує інша точка В, у якій досягається локальний оптимум. У задачах такого типу немає можливості використати обчислювальну процедуру симплексного типу, оскільки вона може привести до локального, проте не обов’язково до глобального оптимуму.

Якщо задача містить нелінійні обмеження, то властивість опуклості множини планів може не виконуватися. Більше того, множина планів може складатися з кількох незв’язаних областей.

Приклад 3. Повна система обмежень має вигляд

х₁ ³ 0, х₂ ³ 0.

Множина планів складається з двох частин, кожна з яких не опукла (рис. 2.5). Якщо множина планів неопукла, може існувати відмінний від глобального локальний оптимуми, навіть при лінійній цільовій функції. Наприклад, функція Z = 5х₁ – 2х₂ має два локальних мінімуми: у кутовій точці В(0; 3,5) Z(B) = 7; у кутовій точці С(3; Ѕ) Z(С) = 16. Глобальний мінімум досягається в кутовій точці В(0; 3,5).

Для задач нелінійного програмування, що мають відмінні від глобального локальні оптимуми, більшість обчислювальних методів дають можливість знайти точку локального оптимуму. Однак у загальному випадку вони не дають змоги встановити, чи збігається вона з точкою глобального оптимуму.

Рис. 2.14

Далі розглядається класична теорія розв’язування оптимізаційних задач, тобто теорія, що грунтується на застосуванні диференційного числення.

Метод множників Лагранжа

Нехай задано задачу нелінійного програмування:

; (2.115)

. (2.116)

При цьому припускається, що функції f(х₁, х₂, ..., х_n) і q_i(х₁, х₂, ..., х_n) неперервні разом зі своїми частинними похідними першого й другого порядку.

Складаємо функцію Лагранжа:

, (2.117)

де L = (l₁, l₂, …, l_m).

Необхідна умова екстремуму функції F(X, L) має вигляд

;

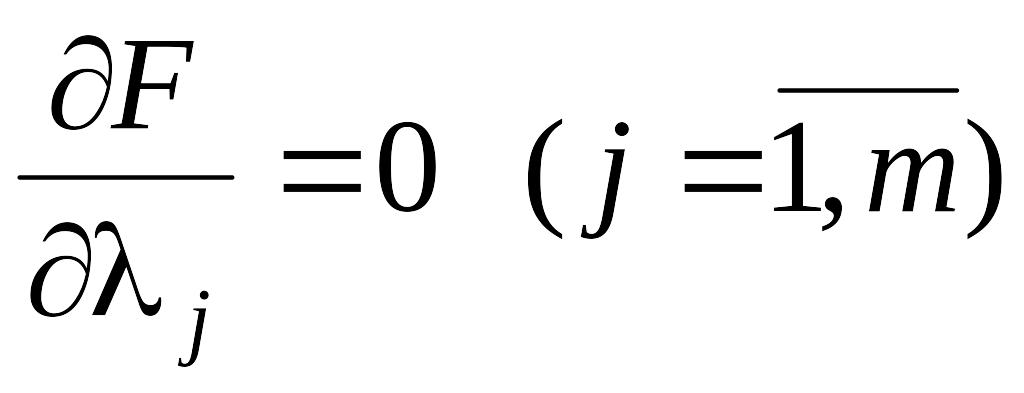
і являє собою систему з n + m рівнянь:

;

. (2.118)

Справедлива наступна теорема, що виражає необхідні умови локального оптимуму задачі (2.115)-(2.116).

Теорема 2.18 Якщо функція Z = f(х₁, х₂, ..., х_n) у точці має екстремум, то існує такий набір , що точка ( ) = =  є розв’язком системи (2.118). (приймемо без доведення).

Точка ( ) називається стаціонарною.

Отримання необхідних умов, яке грунтується на побудові функції F(Х, L) і прирівнюванні до нуля її частинних похідних, називається методом множників Лагранжа. На жаль, для цього методу не існує будь-якого єдиного обчислювального алгоритму розв’язання системи (2.118).

Щоб сформулювати достатні умови локального оптимуму задачі (2.115)-(2.118), які використовуються в ході реалізації методу множників Лагранжа, складемо спеціальним способом матрицю (яку називають обведеною матрицею Гессе) розмірності (n + m) ´ (n + m);

.

або в скороченій формі

.

Достатні умови локального оптимуму задачі (2.115)-(2.116) полягають у наступному. Нехай ( ) – критична точка функції (2.117) і складено матрицю H^B у точці ( ). Тоді є:

1) точкою максимуму, якщо, починаючи з головного мінора порядку (т + 1), знаки наступних (п – т + 1) головних мінорів матриці Н^В чергуються й знак першого мінора визначається множником (–1)^{т + 1};

2) точкою мінімуму, якщо, починаючи з головного мінора порядку (т + 1), знак наступних (п – т + 1) головних мінорів матриці Н^В визначається множником (–1)^т (приймаємо без доведення).

Примітка 1. Ці умови не є необхідними, тобто критична точка, що не задовольняє ці умови, також може бути точкою локального оптимуму.

Примітка 2. Перетворивши матрицю неможна побудувати достатні умови, які будуть і необхідними. Однак їх практична реалізація пов’язана із значними обчислювальними складностями.

Побудуємо матрицю

,

де m – невідомий параметр; Е – одинична матриця п-го порядку. Позначимо визначник метриці через D. Очевидно, що в кожній точці визначник D є многочлен відносно параметра m. Якщо в критичній точці всі дійсні корені цього многочлена від’ємні, то – точка максимуму, якщо додатні, то – точка мінімуму.

Приклад.

;

Розв’язання. Складемо функцію Лагранжа:

.

Щоб знайти критичні точки, отримуємо таку систему рівнянь:

Розв’язавши цю систему, дістанемо стаціонарну точку

( ) = (1, 1, 1, 1, 1).

Обчислимо всі елементи матриці Н^В у цій точці:

; ; ; ; ; ;

; ; ; ; ;

; ; ; .

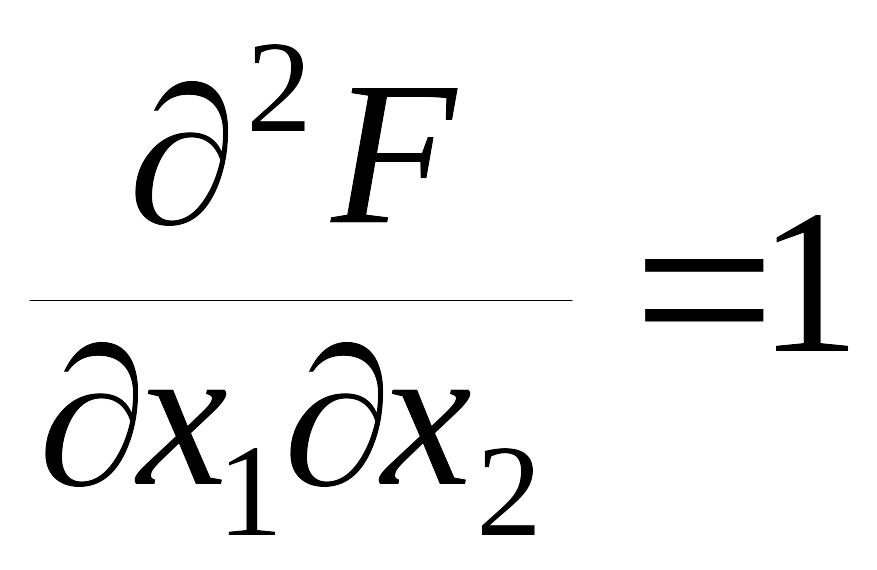Матриця Н^В має вигляд

.

Оскільки m = 2 і n = 3, критична точка є точкою максимуму, якщо мінор 3-го порядку й наступні головні мінори матриці в цій точці утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником (–1). Знайдемо ці мінори:

; ;

.

Отже, ( ) = (1, 1, 1, 1, 1) є точкою локального максимуму функції Лагранжа, тобто ( ) = (1, 1, 1) – оптимальний план задачі й Z_max = 2.

Приклад. Розглянемо таку задачу:

; .

Складемо функцію Лагранжа:

.

Необхідні умови екстремуму цієї функції:

Розв’язавши систему рівнянь, дістанемо три критичні точки:

( ) = (2, 2, 1, 1); ( ) = (2, –2, 1, 1); ( ) = .

Матриця

.

У критичній точці ( )

; ;

; .

Точка ( ) = (2; 2; 1; 1) – точка локального мінімуму.

У критичній точці ( )

; ;

; .

Точка ( ) = (2; –2; 1; 1) – точка локального мінімуму.

У критичній точці ( )

; ;

; .

У критичній точці ( ) = (2,8; 0; 1,4; 1,4) достатня умова не дає змоги визначити, чи є ця точка екстремальною. Скористаємося умовами, сформульованими в примітці 2. Складемо матрицю :

.