Економічні постановки та математичні моделі відкритих транспортних задач

Нехай сумарний попит перевищує пропозицію, тобто 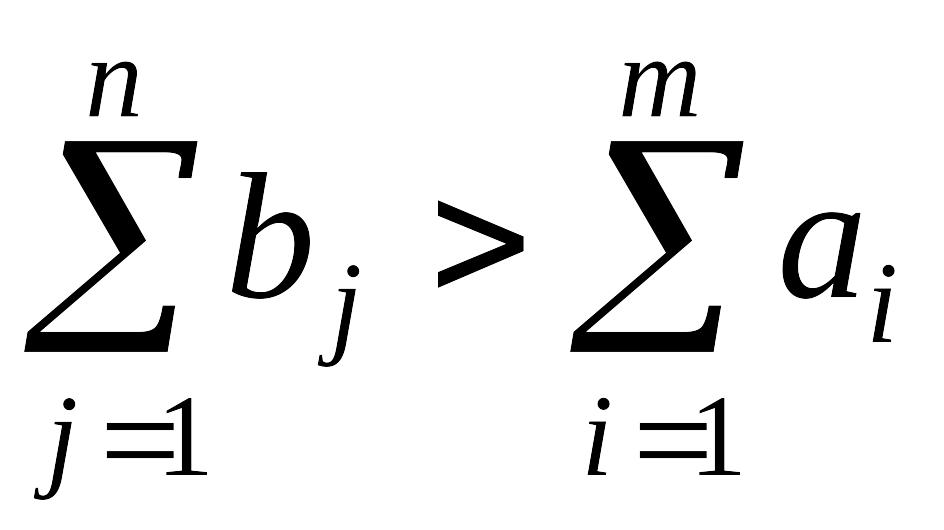. В цьому разі неможливо задовольнити попит усіх споживачів, тому економічна постановка задачі така: скласти план перевезень, за якого весь товар від усіх постачальників вивозиться, попит споживачів по можливості задовольняється (споживачі одержують товари в кількостях, які не перевищують їх попиту) і сумарні транспортні витрати мінімальні.

Розглянемо математичну модель такої задачі.

Увесь товар, який мають постачальники, вивозиться:

. (2.85)

Споживачі одержують товар у кількостях, які менші або дорівнюють попиту на нього:

. (2.86)

Умова невід’ємності (2.83) і цільова функція (2.84) не змінюються

x_ij ³ 0 . (2.87)

. (2.88)

Якщо сумарна пропозиція перевищує сумарний попит 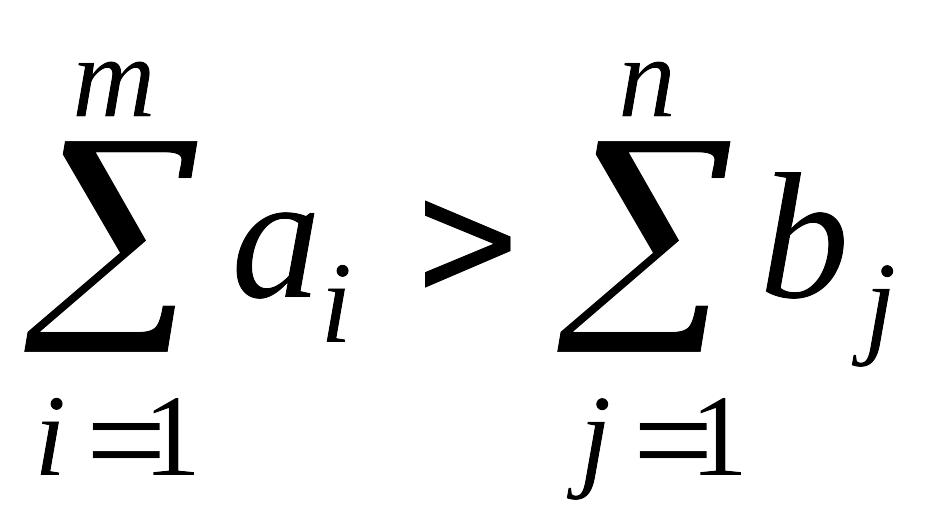, задоволення попиту споживачів не супроводжується повним вивезенням товару від постачальників. Отже, економічна постановка задачі така: скласти план перевезень, за якого потреби всіх споживачі задовольняються, від постачальників вивозяться товари в кількості, до не перевищує їх потужності, й сумарна вартість перевезень мінімальна.

Першу умову задачі можна записати у вигляді

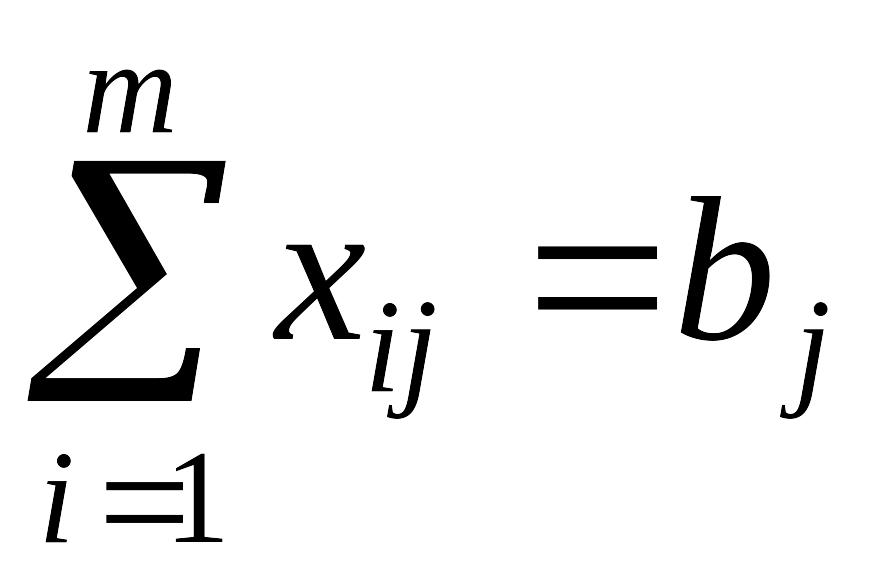; (2.89)

друга умова

. (2.90)

Окрім того, зберігаються умови невід’ємності

x_ij ³ 0 . (2.91)

і цільова функція

. (2.92)

Очевидно, що моделі (2.85)-(2.88) і (2.89)-(2.92) являють собою ЗЛП, задані не в канонічному вигляді. Щоб звести їх до канонічного вигляду, в нерівності (2.86) і (2.90) треба ввести додаткові невід’ємні змінні, які ввійдуть до цільової функції з нульовими коефіцієнтами.

З метою змістовної економічної інтерпретації цих змінних позначимо їх таким чином. У (2.86)

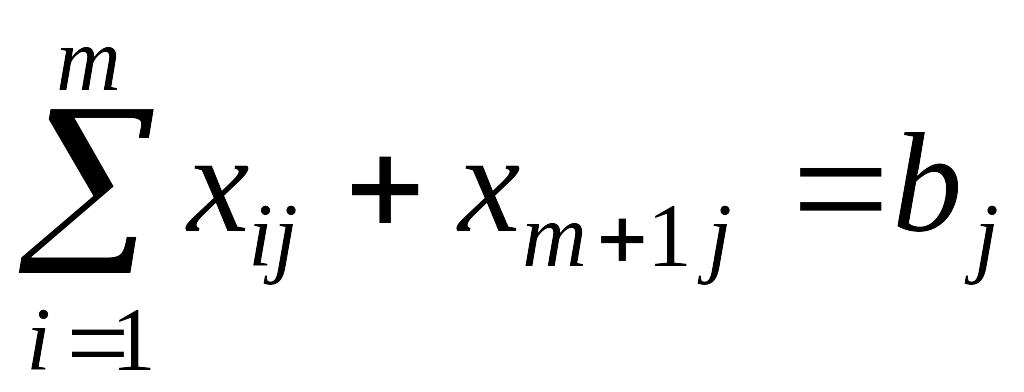; (2.93)

а в (2.90)

. (2.94)

У випадку (2.93) набір {x_{m + 1j}} можна інтерпретувати як поставки від деякого (т + 1)-гo фіктивного постачальника. Оскільки цей товар насправді не існує, вартість перевезення його дорівнює нулю, отже, тарифи перевезень від А_{т + 1} до всіх споживачів дорівнюють нулю. Введення цих додаткових змінних в цільову функцію з використанням коефіцієнтів, які дорівнюють нулю, економічно обгрунтоване. Зазначимо, що величина x_{m + 1j} характеризує попит В_j, який не задовольнили.

Підсумувавши співвідношення (2.93) за j, дістанемо

+ .

Змінивши порядок підсумовування в першому доданку, з урахуванням (2.85) отримаємо

+ ,

або

– .

Ліва частина отриманого співвідношення – це кількість товарів, що вивозяться від А_{т + 1} до всіх споживачів, тобто потужність (т + 1)-го постачальника.

Отже, щоб звести відкриту ТЗ (2.84)-(2.88) до канонічного вигляду, тобто до закритої ТЗ, вводять (т + 1)-го фіктивного постачальника, потужність якого 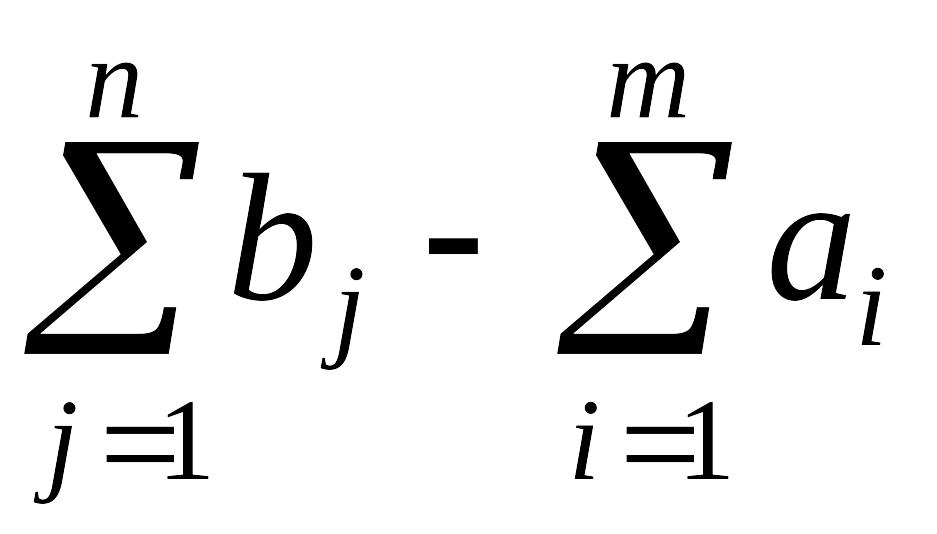, і тарифи перевезень від нього дорівнюють нулю.

Аналогічно з (2.94) випливає, що набір {x_{іп + 1}} можна інтерпретувати як перевезення до деякого (п + 1)-го фіктивного споживача. Неважко показати, підсумовуючи (2.94) за і, що попит В_{п + 1} = . Величина x_{іп + 1} – це кількість товару, що залишився в А_і. Оскільки ці товари не перевозяться, транспортні витрати для них дорівнюють нулю, отже, тарифи перевезень до фіктивного споживача можна вважати такими, що дорівнюють нулю.

Отже, ввівши фіктивного споживача чи постачальника, відкриту ТЗ можна звести до закритої й таким чином звести задачу до канонічної форми. Тому, так само як і в загальній теорії лінійного програмування надалі під ТЗ розумітимемо закриту ТЗ, яка задається співвідношеннями (2.81)-(2.82), вважаючи, що серед А_і і В_j можуть бути й фіктивні.

Задача (2.81)-(2.84) є ЗЛП, отже, для неї справедливі всі означення та властивості ЗЛП, розглянуті в попередніх розділах. Оскільки клас ТЗ вужчий від класу ЗЛП, він має ряд специфічних особливостей, що дають змогу спростити означення, а також виробити досить прості методи розв’язування. Одна з важливіших особливостей ТЗ полягає в тому, що будь-яка ТЗ має розв’язок.