Тема 4. Теорія двоїстості та аналіз лінійних оптимізаційних задач Поняття двоїстості

Теорія двоїстості – центральна частина лінійного програмування. Дослідження двоїстості дало можливість отримати важливі теоретичні (розробити ефективні методи розв’язування ЗЛП, проаналізувати та оцінити чутливість моделей лінійного програмування) і практичні (дати економічне тлумачення отриманого розв’язку, розкрити нові закономірності та співвідношення, властиві досліджуваній проблемі) результати.

На початковій стадії дослідження задач лінійного програмування виявили, що кожній ЗЛП відповідає інша, цілком визначена ЗЛП, тобто ці задачі взаємопов’язані: якщо вихідною вважати другу, то їй відповідатиме перша. Крім того, взаємозв’язок настільки тісний, що в ході розв'язування одної з них фактично, як буде показано далі, розв’язується й інша задача. Ця пара була названа двоїстою (спряженою) парою задач.

Розглянемо конкретну задачу (дані умовні).

Приклад. На деякому підприємстві виробляють продукцію народного споживання. Припустимо, що підприємство має чотири види ресурсів у кількості 15, 18, 6, 8 од. і намічає випуск двох видів виробів. Затрати ресурсів на виробництво одиниці продукції першого виду становлять відповідно 3, 2, 4, 1І од., другого – 3, 6, 0, 2 од.

Очікуваний прибуток від реалізації продукції народного споживання першого виду - 20 грн., другого - 30 грн. Треба розробити план виробництва, що забезпечує підприємству найбільший прибуток від реалізації цих виробів.

Складаємо математичну модель задачі. Для цього вводимо змінні:

х₁, х₂ - кількість одиниць продукції відповідно першого й другого виду, яку треба виробити за шуканим планом; Z - прибуток від реалізації всієї виробленої продукції народного споживання.

Формалізоване подання мети розв'язування задачі, тобто цільова функція, має вигляд

Z = 20x₁ +30x₂ (max). (2.54)

Умови, що обмежують досягнення мети, - обсяги використання чотирьох видів ресурсів. У зв’язку з цим складемо чотири обмеження, кожне з яких виражає наступне: витрата ресурсу певного виду для виконання плану виробництва продукції не повинна перевищувати його наявного обсягу:

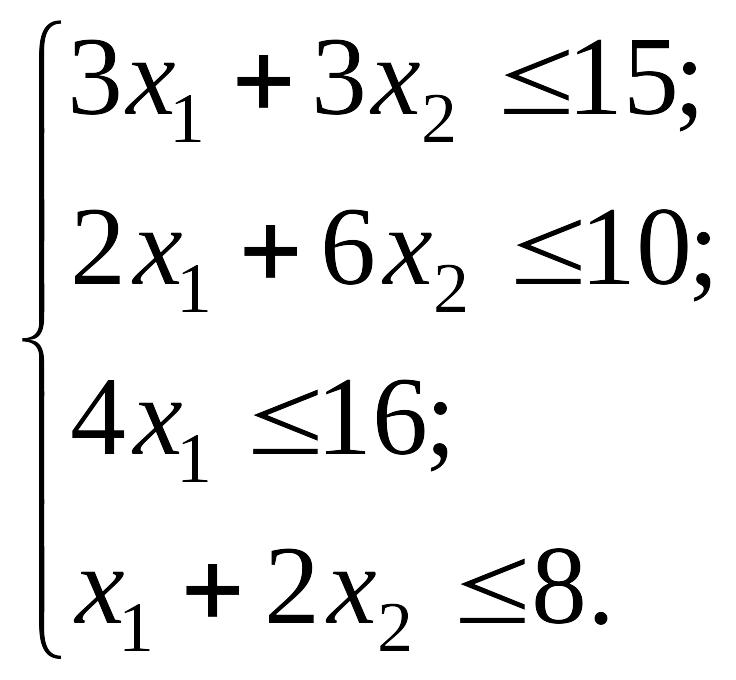(2.55)

Із економічного смислу введених змінних х₁ і х₂ випливає їх невід’ємність:

х₁ ³ 0; х₂ ³ 0. (2.56)

Співвідношення (2.54)-(2.56) – математична модель задачі. Вважатимемо що задачу вихідною та сформулюємо для неї двоїсту задачу.

Припустимо, що в ході вивчення питання про використання ресурсів на підприємстві з’явилась можливість реалізувати їх іншому підприємству. При цьому підприємство-покупець вважає за необхідне розглянути різні варіанти цін на них, але вимагає, щоб загальна вартість ресурсів. була мінімальною.

Уведемо позначення: у₁ – передбачувана ціна одиниці першого ресурсу; у₂ - другого; у₃ – третього; у₄ – четвертого; f - загальна вартість ресурсів.

Тоді вимогу покупця запишемо у вигляді

f = 15у₁ + 18у₂ +16у₃ + 8у₄ (min) (2.57)

Очевидно, що реалізовувати ресурси доцільно лише в тому разі, коли виручка від продажу такої кількості ресурсів, із яких можна виготовити одиницю продукції, не менша, ніж прибуток від реалізації самого виробу:

3у₁ + 2у₂ + 4у₃ + у₄ ³ 20;

3у₁ + 6у₂ + 2у₄ ³ 30. (2.58)

Ціни не можуть бути від’ємними:

у₁ ³ 0; у₂ ³ 0; у₃ ³ 0; у₄ ³ 0. (2.59)

Співвідношення (2.57)-(2.59) – математична модель двоїстої задачі відносно задачі (2.54)-(2.2.56); у₁, у₂, у₃, у₄ - шукані ціни на ресурси. Вони відносні, по-перше, з точки зору доходів, отримуваних підприємством у процесі переробки ресурсів у готову продукцію, а по-друге, змінюються зі зміною обсягів ресурсів.

Розглянемо загальний випадок задачі раціонального використання ресурсів.

Для виробництва п видів продукції витрачається т видів ресурсів. Відомо:

a_ij - норма витрати і-го виду ресурсів на одиницю продукції j-го виду (і =  ); (j = ).

b_i - запас ресурсу і-го виду на запланований період (і =  );

с_j - прибуток від реалізації одиниці продукції j-го виду (j = )..

Скласти план виробництва, що забезпечує максимальний прибуток.

Уведемо позначення: х_j - запланований випуск продукції j-го виду; Z - прибуток від реалізації всієї виробленої продукції.

Математична модель задачі. Знайти такі х_j, які забезпечують максимум функції

Z = c₁х₁ + с₂х₂ + … + с_nx_n (max) (2.60)

і задовільняють обмеження

(2.61)

. (2.62)

Економічна інтерпретація цієї задачі: скільки та якої продукції треба виробити, щоб при заданих обсягах ресурсів, які витрачаються, максимізувати прибуток.

Складемо математичну модель і дамо економічну інтерпретацію двоїстої задачі відносно задачі (2.60)-(2.62).

Нехай у_і - ціна одиниці ресурсу і-го виду (і =  ), тоді вартість усіх ресурсів

f = b₁y₁ + b₂y₂ + ... + b_my_m.

Прибуток від продажу ресурсів, потрібних для випуску одиниці j-го виробу, має бути не меншим за прибуток від реалізації готового виробу:

a_1jy₁ + a_2jy₂ + … +a_mjy_m ³ c_j.

Отже, двоїсту задачу можна сформулювати так. Знаючи у₁, у₂, ..., у_т, які надають мінімуму функції

f = b₁y₁ + b₂y₂ + ... + b_my_m (min) (2.63)

і задовольняють обмеження

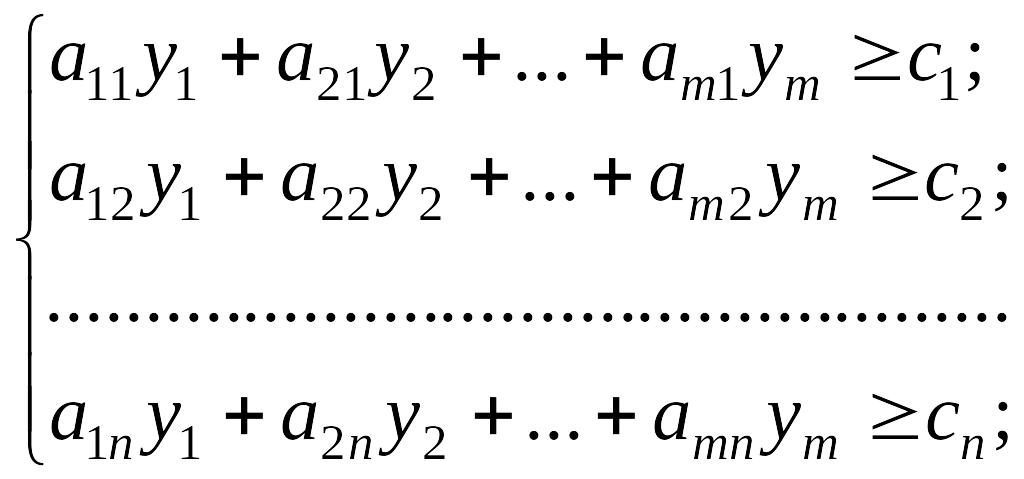(2.64)

. (2.65)

Економічна інтерпретація двоїстої задачі: якими мають бути ціни одиниці ресурсів, щоб при заданих обсягах ресурсів (b_i) і прибутку від реалізації одиниці продукції (с_j) мінімізувати загальну вартість ресурсів; у_і називаються оцінками, або обліковими, неявними цінами. Ці оцінки (ціни) - відносні, оскільки одні й ті самі ресурси для різних підприємств мають різну цінність, а оцінки ресурсів для того самого підприємства також змінюються зі зміною обсягів ресурсів. Відносність оцінок обумовлена ще й тим, що вони виражаються в одиницях вартості продукції, що випускається.

Види двоїстих пар задач

Аналізуючи математичні моделі наведених двоїстих пар задач (2.54)-(2.56) і (2.57)-(2.59), (2.60)-(2.62) і (2.63)-(2.65), можна встановити зв’язок між математичними моделями цих задач і вказати етапи формальної побудови математичної моделі однієї із задач за відомою моделлю іншої.

Для цього запишемо математичні моделі задачі раціонального використання ресурсів і двоїстої відносно неї задачі в матричному вигляді. Введемо матриці:

С = (с₁, с₂, ..., с_n) – матриця-рядок, складена з коефіцієнтів цільової функції вихідної задачi;

- матриця-стовпець, складена зі змінних вихідної задачі;

– матриця, складена з коефіцієнтів при змінних у основній системі обмежень вихідної задачі;

- матриця-стовпець, складена з вільних членів основної системи обмежень вихідної задачі;

Y = (y₁, y₂, …, y_n) – матриця-рядок, складена зі змінних двоїстої задачі.

Задача (2.60)-(2.62) (вихідна) запишеться так:

Z = C×X (max); (2.66)

A×X £ B; (2.67)

X ³ 0. (2.68)

Задача (2.63)-(2.65) (двоїста) запишеться так:

f = y×B (min); (2.69)

Y×A ³ С; (2.70)

Y ³ 0. (2.71)

Із зіставлення математичних моделей двоїстих пар задач у розгорненій і матричній формах, випливає, що для формальної побудови математичної моделі одної з двоїстої пари задач за відомою моделлю іншої задачі треба (поетапно):

1) поміняти місцями вільні члени основної системи обмежень і коефіцієнти цільової функції;

2) транспонувати матрицю коефіцієнтів при змінних основної системи обмежень;

3) змінити знаки нерівностей системи основних обмежень „£”, на „³", і навпаки, й вигляд екстремуму цільових функцій на протилежний: мінімум на максимум.

Розрізняють симетричні та несиметричні пари двоїстих задач. Якщо системи основних обмежень як у вихідній, так і в двоїстій задачі мають вигляд нерівностей, то такі пари двоїстих задач називатимемо симетричними. При цьому на змінні двоїстої задачі також накладається умова невід’ємності.

Пара задач (2.66)-(2.68) і (2.69)-(2.71) є симетричною.

Можна виділити два види математичних моделей симетричної пари двоїстих задач.

1. Вихідна задача Двоїста задача

Z = C×X (max); f = y×B (min); (2.72)

A×X £ B; Y×A ³ С;

X ³ 0. Y ³ 0.

2. Вихідна задача Двоїста задача

Z = C×X (min); f = y×B (max); (2.73)

A×X ³ B; Y×A £ С;

X ³ 0. Y ³ 0.

Якщо система основних обмежень вихідної задачі має вигляд рівнянь, а двоїстої - вигляд нерівностей однакового смислу, то таку двоїсту пару називатимемо несиметричною двоїстою парою. На змінні двоїстої задачі не накладається умова невід’ємності.

Несиметричні двоїсті пари задач також бувають двох видів.

3. Вихідна задача Двоїста задача

Z = C×X (max); f = y×B (min); (2.74)

A×X = B; Y×A ³ С.

X ³ 0.

4. Вихідна задача Двоїста задача

Z = C×X (min); f = y×B (max); (2.75)

A×X = B; Y×A £ С.

X ³ 0.

У разі побудови несиметричної пари змінюється третій етап. Оскільки у вихідній ЗЛП обмеження – рівняння, знаки нерівностей у двоїстій задачі визначаються видом екстремуму. Якщо f ® max, то обмеження „£”, якщо f ® min, то „³".

Щоб побудувати математичну модель двоїстої задачі за відомою моделлю вихідної задачі, треба математичну модель вихідної задачі перетворити до одного з чотирьох указаних видів.

Приклад. Побудувати математичну модель двоїстої задачі для задачі

;

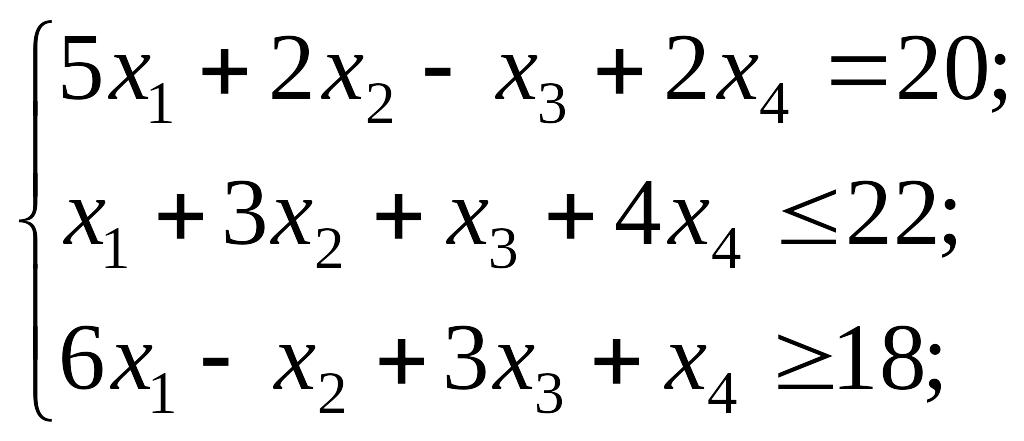
х₁ ³ 0; х₂ ³ 0; х₃ ³ 0; х₄ ³ 0.

Якщо в системі основних обмежень вихідної задачі є хоча б одне рівняння, можна побудувати лише несиметричну двоїсту пару задач. Для цього друге й третє обмеження введенням додаткових невід’ємних змінних перетворимо в рівняння. Математична модель задачі набуває вигляду

;

х_j ³ 0 .

Математичну модель вихідної задачі перетворено до вигляду (2.74). Тоді математична модель двоїстої задачі має вигляд

f = 20y₁ + 22y₂ + 18y₃ (min)

Примітка. Отримана задача не є ЗЛП у загальноприйнятому розумінні. В ній змінна у₃ недодатна, а на у₁ жодної умови на знак не накладається. Однак замінивши змінні у₁ = u₁ – u₂, у₂ = u₃, у₃ = –u₄, цю задачу можна перетворити до вигляду

f = 20u₁ – 20u₂ + 22u₃ – 18u₄ (min);

u_i ³ 0 ,

що є ЗЛП.

Побудова математичної моделі одної з двоїстих задач за відомою іншою особливої складності не становить. Складніше дати економічну інтерпретацію двоїстої задачі в термінах вихідної.

Оскільки ЗЛП із системою обмежень у вигляді нерівностей введенням додаткових невід" ємних змінних можна перетворити в ЗЛП із системою обмежень у вигляді рівнянь, будь-яку симетричну двоїсту пару задач можна перетворити у несиметричну.

Отже, ми ввели поняття двоїстості, вигляди двоїстих пар задач, зв’язок між їх математичними моделями. Розглянемо істотніші зв’язки, а саме зв’язки між планами й розв'язками двоїстих пар задач. Ці зв'язки встановлюють теореми теорії двоїстості.