Метод штучного базису (м-метод).

Метод штучного базису використовують для розв’язування ЗЛП, у яких серед відповідних векторів немає ортонормованого базису.

У цьому разі в кожне з рівнянь уводять невід’ємну змінну з коефіцієнтом 1. Вона називається штучною, а вектор, що їй відповідає, який, очевидно, буде ортом, також називається штучним.

Отже, якщо задано ЗЛП

; (2.48)

(2.49)

. (2.50)

то після введення штучних змінних повна система обмежень набував вигляду

(2.51)

. (2.52)

Очевидно, що отримана система нерівносильна початковій (2.49)-(2.50). Однак якщо ця система має розв’язки, в яких штучні змінні дорівнюють нулю, то перші п, їх компонент будуть розв'язком системи (2.49)-(2.50), тобто планом ЗЛП (2.48)-(2.50). Зокрема, якщо буде знайдено оптимальний розв’язок нової задачі, в якому штучні змінні дорівнюють нулю, то перші п, компонент цього плану є оптимальним планом початкової задачі (це буде доведено далі). Таким чином, з'являється така схема розв’язання.

Штучні змінні за смислом свого введення є базисними, тобто всі вони або деякі з них додатні. Для того щоб вони дорівнювали нулю, достатньо перетворити їх у вільні, тобто вивести вектори з базису. З цією метою штучні змінні вводять у цільову функцію з умовними коефіцієнтами М, де М – нескінченно велике число (число, більше від будь-якого іншого, з яким його доводиться зрівнювати):

; (2.53)

У цьому випадку доти, доки всі штучні змінні не обнуляться, значення Z^M буде нескінченно великим, тобто відповідні плани не будуть оптимальними. Крім того, коефіцієнти в цільовій функції гарантують те, що штучні вектори не вводитимуть у базис, якщо на попередніх ітераціях вони були виведені з базису.

Задача (2.51)-(2.53) називається розширеною або M-задачею відносно початкової задачі (2.48)-(2.50). Зв’язок між розв'язками цих задач установлює така теорема.

Теорема 2.14 Якщо в оптимальному плані М задачі всі штучні змінні дорівнюють нулю, то набір решти змінних є оптимальним планом початкової задачі. Значення цільової функції при цьому збігаються.

Зауваження. Раніше було доведено, що М-задача не може мати розв’язку, в якому хоча б одна штучна змінна більша від нуля. Однак розв’язуючи її CM, зокрема, на ЕОМ, коли як М вибирають велике, але скінченне число, формально, якщо оцінки всіх коефіцієнтів недодатні, процедуру припиняють. Цей випадок, а також випадок необмеженості цільової функції (існує вектор з додатною оцінкою, компоненти якого недодатні) інтерпретуються як неможливість виведення з базису всіх штучних векторі рів, тобто відсутні плани початкової ЗЛП: K ¹ Æ, ЗЛП нерозв’язувана.

Задача. Розв’язати ЗЛП М-методом.

Оскільки в першому рівнянні є змінна , якої немає в решти, перше рівняння ділимо на 2. У другому обмеженні введемо додаткову змінну . У третьому рівнянні відсутня змінна, аналогічна у першому, тому введемо штучну змінну . У четвертому обмеженні введемо додаткову змінну x₇ із знаком “-” і штучну змінну . Дістанемо М-задачу

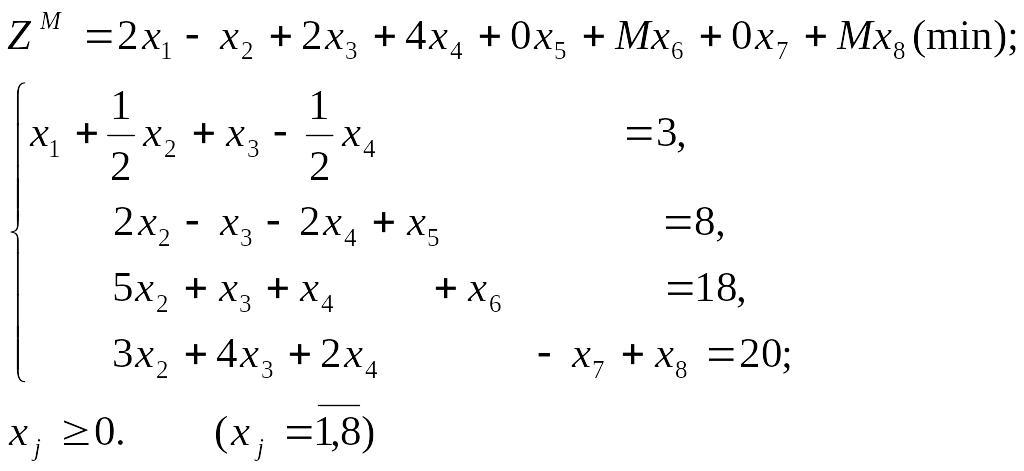
Ортонормований базис утворюють вектори , , , . Отже, початковий опорний план має вигляд

Розв’яжемо задачу СМ. Єдина відмінність розв’язку М-задачі від розв’язку звичайних ЗЛП полягає в тому, що в рядку оцінок окрім чисел фігурує число М.

Перша симплексна таблиця має вигляд:

Б	СБ		2	-1	2	4	0	М	0	М	4	2	3
	2	3	1		1		0	0	0	0	-		3
	0	8	0	2	-1	-2	1	0	0	0	-	4	-
	М	18	0	5	1	1	0	1	0	0	18		18
	М	20	0	3	4	2	0	0	-1	1	10	2 0 3	5
		38М+6	0	8М+2	5М	3М-5	0	0	-М	0	30М-50	12М+2	15М

Оскільки оцінки векторів , і більші від 0, план неоптимальний. Зазначимо, що оцінка більша від 0, оскільки М- нескінченно велике число, і якщо коефіцієнт при М додатний, то в процесі віднімання будь-якого числа результат буде додатним.

Введемо в базис вектор . Його оцінка, зважаючи на коефіцієнт при М менша від та , однак у процесі пошуку величин стає очевидним, що вектор увійде в базис замість штучного вектору , а саме цього треба добиватися в першу чергу. Для спрощення системи розрахунків дещо відійшли від симплексних процедур зміни базису.

Друга таблиця має вигляд:

Б	СБ		2	-1	2	4	0	М	0	М
	2	8	1		2	0	0	0	-		-
	0	28	0	5	3	0	1	0	-1	1	-
	М	8	0		-1	0	0	1			16
	4	10	0		2	1	0	0			-
		8М+56	0	М+	-М+10	0	0	0

Новий план також неоптимальний. Введемо в базис вектор , хоча його оцінка менша, ніж у , проте очевидно, що він витиснить із базису останній штучний вектор .

Третя таблиця:

Б	СБ		2	-1	2	4	0	М	0	М
	2	12	1	3		0	0		0	0	4
	0	44	0	12	1	0	1	2	0	0
	0	16	0	7	-2	0	0	2	1	-1
	4	18	0	5	1	1	0	1	0	0
		96	0	27	5	0	0		0	-М

План неоптимальний, однак головним є те, що штучні змінні в ньому , тобто отримано план початкової ЗЛП. Оцінки векторів і від’ємні, оскільки в них входить «-М» і процедура СМ не вимогатиме введення їх у базис.

Четверта таблиця:

Б	СБ		2	-1	2	4	0	М	0	М
	2		1	0		0	0
	0		0	0		0	1
	-1		0	1		0	0				-
	4		0	0		1	0
			0	0		0	0

План неоптимальний. Введемо в базис і виводимо :

П’ята таблиця:

Б	СБ		2	-1	2	4	0	М	0	М
	2			0	1	0	0
	0			0	0	0	1
	-1			1	0	0	0
	4			0	0	1	0
				0	0	0	0

В останній таблиці отримано оптимальний план

;

.

Відкинувши штучні змінні, дістанемо розв’язок початкової задачі:

;

.

Зауваження.

В ході побудови М-задачі для ЗЛП з максимізацією функції, штучні змінні вводять у систему обмежень так само, як і в задачах мінімізації, а в цільову функцію вони входять з коефіцієнтами “–М”, що перешкоджає досягненню максимуму.