Оцінка оптимальності опорного плану.

Означення 2.12. Числа називають оцінками векторів або оцінками плану.

Теорема (ознака неоптимальності невироджених опорних планів). Якщо для деякого опорного невиродженого плану існує вектор з додатною оцінкою , то не є оптимальним планом, тобто можна побудувати план Х^’, l-та компонента якого перевищує нуль і для нього .

Теорема 2.11. (достатня ознака оптимальності опорних планів). Якщо для деякого опорного плану оцінки всіх векторів недодатні ( , то оптимальний план.

Примітка. Ця теорема справджується також для вироджених планів. Якщо – невироджений опорний план, то достатня ознака оптимальності є й необхідною.

Перехід від одного опорного плану до іншого розглянемо в алгоритмі

2.3.3 Алгоритм симплексного методу.

Розглянемо на слідуючій умовній задачі.

Задача. Розв’язати ЗЛП симплексним методом.

Знайдемо початковий опорний план, для цього перетворимо задачу до канонічного вигляду:

Серед цих трьохвимірних векторів є три одиничних А₄ А₅ А₆ . Вони утворюють базис, тому змінні х₄ ,х₅, х₆ – базисні, а х₁, х₂ – не базисні, тому початковий опроний план має вигляд Х₀=(0,0,1,2,5). Заповнюємо першу симплексну таблицю.

Загальна характеристика симлексної таблиці. В столбці Б записуються вектори ,які входять до базису. В столбці С_б записується коефіціенти цільової функції при базисних змінних (0,0,0). В столбці А₀ записуються значення базисних змінних опорного плана. В столбцях А_j записуються коефіцієнти розгдяду відповідного вектору за векторами базису. Зауваження:так як початковий базис ортонормований і коефіцієнти розгляду будь-якого вектору за векторами ортонормованого базису, співвпадають з його компонентами таблицями , то в першій симплексній таблиці в столбцях А_j записуються компоненти відповідних векторів. Рядок Z_j – С_j – називається індексним рядком і в ньому запис:

• на перетині зі столбцем А₀ – значення цільової функції для цього опорного плану, яке дорівнює сумі добутків елементів стовпця С_б на відповідні елементи стобця А₀

Z = 0*1+0*2+0*5

• На перетині зі столбцями А_j записується оцінки векторів Z_j – С_j , які дорівнюють сумі добутків елементів стовпця С_б на відповідні елементи стовпця А_j мінус коефіцієнти цільової функції С_j .

Z_j – С_j = 0*2+0*(-4)+0*3-1

Б	СБ		1	-1	-3	0	0	0
	0	1	2	-1	1	1	0	0	-	1
	0	2	4	2	-1	0	1	0	1	-
	0	5	3	0	3	0	0	1	-
		0	-1	1	3	0	0	0	1	3

Ортонормований базис складають вектори , , , отже, початковий опорний план має вигляд

Складаємо першу симплексну таблицю:

План неоптимальний, оскільки та . Серед компонент й існують додатні, отже, ЗЛП розв’язувана. Переходимо до нового опорного плану. Для цього заповнюються стовпці і , діленням елементів стовпця “ ” на відповідні додатні елементи стовпців і . Найменші числа в (виділені діагональною штриховкою) множаться на відповідну оцінку і результат заносимо у відповідні комірки рядку “ ”. Найбільший по модулю добуток визначає вектор, який виводиться з базису ( ) і вектор, який вводиться в базис замість ( ). Відповідний стовпець і відповідний рядок називаються ключовими. Елемент, який знаходиться на перетині ключових рядка і стовпця називається розв’язувальним елементом. Таким чином перехід від одного опорного плану до другого означає перехід від одного базису до іншого, при цьому один із векторів попереднього базису виводиться, якому відповідає з найбільшою по модулю *(Z_j – С_j ) , на його місце вводиться вектор, якому відповідає оцінка з найбільшим по модулю добутком. Так одержимо новий базис (А₃ А₅ А₆).

Складаємо другу симплексну таблицю. Правило перерахунку елементів другої та наступних симплексних таблиць:

1. Елементи стовпців “Б” і “С_Б” заповнюються відповідно до аналізу попередньої таблиці;

2. Елементи ключового рядку ділимо на розв’язувальний елемент;

3. Якщо вектор у базисі, то на перетині рядка, що відповідає базисному вектору з одноіменним стовпцем, залишають одиницю, а решта елементів стовпця дорівнює нулю.

4. Інші елементи, включаючи індексний рядок, обчислюють за формулою:

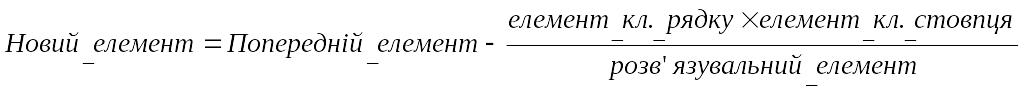
5. Якщо в ключовому рядку (стовпці) стоїть 0, то відповідний стовпець (рядок) переписується без змін.

Б	СБ		1	-1	-3	0	0	0
	-3	1	2	-1	1	1	0	0	-
	0	3	-2	1	0	1	1	0	3
	0	2	-3	3	0	-3	0	1
		-3	-7	4	0	-3	0	0

Наведемо приклад перерахунку елементів симплексної таблиці:

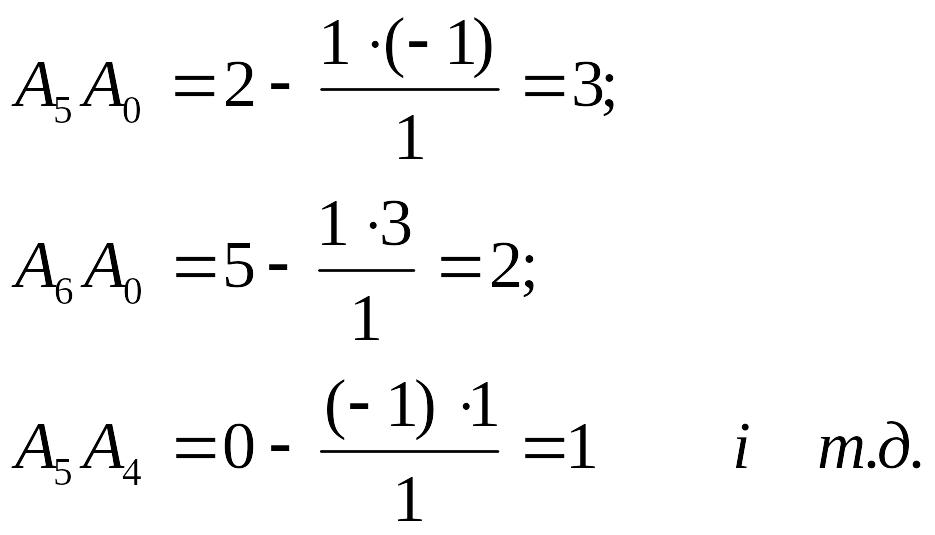
Опорний план неоптимальний. ЗЛП розв’язувана. Вектор вводять у базис, а вектор виводять.

Складаємо третю симплексну таблицю:

Б	СБ		1	-1	-3	0	0	0
	-3		1	0	1	0	0		-
	0		-1	0	0	2	1
	1		-1	1	0	-1	0		-
			-3	0	0	1	0

Опорний план неоптимальний. Вектор вводять у базис, а вектор виводять.

Складаємо четверту симплексну таблицю:

Б	СБ		1	-1	-3	0	0	0
	-3		1	0	1	0	0
	0			0	0	1
	1			1	0	0
				0	0	0

Усі оцінки недодатні, отже, - оптимальний план

Процедуру СМ розглядали стосовно ЗЛП, заданої в стандартній формі канонічного вигляду, що, зокрема, передбачає мінімізацію цільової функції. Разом із тим існують економічні постановки задач, що зводяться до ЗЛП на максимум цільової функції, для яких технічно простий перехід до задачі мінімізації призводить до втрати економічного смислу не лише кінцевого, а й проміжних результатів.

Водночас процедура СМ для задачі максимізації відрізняється від процедури мінімізації лише на етапах оцінки оптимальності, розв’язності й вибору вектора, який вводять у базис при переході до кращого плану. Сформулюємо відповідні теореми.

Теорема 2.12 (ознака неоптимальності опорних невироджених планів ЗЛП, що розв’язується на максимум цільової функції).

Якщо для деякого опорного невиродженого плану існує вектор з від’ємною оцінкою ( ), то план неоптимальний, тобто можна побудувати план у якого l-та компонента більше від 0, а значення цільової функції більше, ніж у вихідного плану.

Ця теорема встановлює також процедуру покращення плану: в базис треба вводити вектор з від’ємною оцінкою.

Теорема 2.13 (достатня ознака оптимальності опорних планів ЗЛП, що розв’язується на максимум цільової функції).

Якщо для деякого опорного плану оцінки векторів невід’ємні, план оптимальний. Формулюємо також ознаку необмеженості цільової функції в задачах максимізації. Якщо для деякого опорного плану існує вектор, оцінка якого від’ємна й усі коефіцієнти його розкладання за базисом недодатні, то цільова функція необмежена зверху, ЗЛП розв’язку немає.