7. Сетевая и иерархическая модели данных. Операции в сетевой и иерархической базах данных.

Иерархическая модель данных.  Иерархической модели данных соответствует дерево – связной ориентированный граф, который не содержит циклов. В дереве выделяется корень – вершина, в которую не заходит ни одно ребро, а исходит произвольное количество ребер. Ориентация ребер обычно определяется от корня.  В иерархической модели данных между записями двух типов выполняется групповое отношение . Владелец группового отношения – родительская запись, а члены группового отношения – дочерние записи.  Корневая запись каждого дерева обязательно должна содержать ключ с уникальным значением. Ключи некоторых записей должны иметь уникальное значение только в рамках группового отношения. Каждая запись идентифицируется полным ключом, под которым понимается совокупность ключей всех записей от корневой до искомой по иерархическому пути.  Иерархическая модель данных позволяет непосредственно реализовывать связи со степенями один - ко - многим (1:N) и один - ко - одному (1:1). Для реализации связи со степенью многие – ко – многим (M:N) необходимо производить дублирование деревьев.  Над данными в иерархической модели определены следующие основные операции:  - добавлять в базу данных новую запись с обязательным формированием значения ключа для корневой записи;  - изменять значения данных, причем ключевые значения данных не должны подвергаться изменениям;  - удалять некоторую запись и все подчиненные ей записи;  - извлекать ключевую запись по ключевому значению;  - извлекать следующую запись (следующая запись извлекается в порядке левостороннего/правостороннего обхода дерев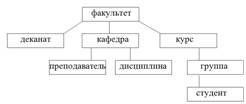а).  Для поиска выборки экземпляров записей типа "студент” надо указать корневой элемент – факультет; элементы – курс и группа.

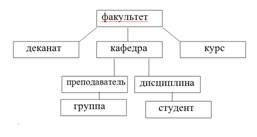
Сетевая модель данных

Сетевой модели данных в общем случае соответствует произвольный граф. В узлах графа помещаются типы записей, а ребра интерпретируются как связи между типами записей.  В сетевой модели данных также как и в иерархической используется графический способ представления данных, но ограничения на количество связей не накладывается. То есть можно изображать модели любой сложности.  Операции над типами записей в сетевой модели данных можно разделить на две основные группы:  1. операции с записями в наборе:  нахождение конкретной записи в наборе;  создание новой записи;  уничтожение записи;  модифицирование записи.  2 . операции навигации:  переход от предка к потомку по некоторой связи;  переход к следующему потомку в некоторой связи;  переход от потомка к предку по некоторой связи;  включение в связь;  исключение из связи;  перестановка в другую связь и т.д. 

8. Отображение сетевой и иерархической баз данных на структуры памяти. Отображение сетевой и иерархической баз данных в реляционную.

9. Способы ускорения доступа к данным. Индексы и методы их построения.

Ускорение доступа к данным достигается применением принципиально иных методов размещения информации, и ее поиска. Для этого создаются массивы вспомогательной информации о хранимых данных.

Эти же методы необходимы при организации доступа к информации по нескольким ключевым атрибутам одновременно.

Доступ к требуемым записям может осуществляться не только путем сравнения искомого значения ключа с ключами записей, извлекаемых из массива по определенному алгоритму (как это было в рассмотренных методах обработки данных), но и в результате вычисления местоположения требуемой записи. Сами записи могут быть упорядочены алгоритмом сортировки либо используется специальная расстановка записей.

6.1 Адресная функция

Расстановка записей происходит в соответствии с так называемой адресной функцией (другие общеупотребительные ее названия - "рандомизирующая функция" или"хэш-функция" от hashing – рассеянная память от глагола to hash – крошить рубить и делать из этого месиво ).

Идея хеширования состоит в использовании некоторой частичной информации, полученной из ключа. В качестве основы поиска. Вычисляется хеш-адрес F(p) и используется для проведения поиска.

Рассмотрим знаменитый пример «парадокс дня рождения». Который обсуждался математиками в 30-е годы. Например, в компании из 23 человек более всего вероятно совпадение дней рождения у двух человек, чем то что у всех дни рождения окажутся различеиные. Иными словами, если выбрать случайную функции, отображающую 23 ключа в таблицу размером 365, вероятность, что никакие два ключа не будут отображены в одно и тоже место таблицы , составляет 0,4927, т.е. менее половины. Этот пример предупреждает нас, что вероятно найдутся различныеключи Pi ¹ Pj при которых F(pi)=F(pj). Такое событие именуется коллизией. Для разрешения коллизий разработаны некоторые подходы.

Поэтому для использования хеширования программист должен решить две практических задачи – выбрать хеш-функцию f(p) и способ разрешения коллизий.

Адресной функцией или хеш функцией называется зависимость

i= f(p),

где i— номер (адрес) записи;

р - значение ключевого атрибута в записи.

К функции f предъявляются следующие требования:

• она должна быть задана аналитически и вычисляться достаточно быстро;

• ключевые атрибуты, подчиняющиеся произвольному распределению, функция должна переработать в равномерно распределенные номера записей; это условие обычно соблюдается приближенно;

• число записей-синонимов или коллизий должно составлять 10-20% от общего числа записей.

Для ускорения поиска записей в массиве используется дополнительная информация, организованная в виде массива индексов.

Индексом называется набор ключей и адресов записей, которые выбираются из основного массива по определенному закону. Отдельный элемент набора индексов также называется индексом, хотя это не соответствует значению слова таех -список.

Имеются три важные разновидности индексов:

• информация о каждой записи основного массива попадает в индекс (сплошная индексация);

• номера записей, информация о которых выносится в индекс, образуют арифметическую прогрессию с шагом d > 1. Основной массив, дополненный таким индексом, обычно называется индексно-последовательным;

• ключи записей, информация о которых выносится в индекс, приближенно образуют арифметическую прогрессию.

Сплошной индекс связан с созданием инвертированного массива ключевых атрибутов к основному массиву. Этот случай рассмотрен в теме ИПС, инвертированные файлы.

Индексно-последовательный массив представляет собой последовательный массив, отсортированный по значениям ключевого атрибута, к которому создается дополнительный массив индексов.

В индекс выносится информация о записях, номера которых образуют арифметическую прогрессию с шагом d. На рис. 6.5 показаны ключевые атрибуты основного массива и состояние массива индексов для d=3

Рис. 6.5. Индексно-последовательная организация данных

Поиск значения q в индексно-последовательном массиве происходит в две стадии:

• в массиве индексов (который отсортирован в силу упорядоченности основного массива);

• среди записей основного массива, расположенных между двумя соседними индексами, найденными на первой стадии.

Применение индексов приводит к ускорению доступа, если основной массив располагается на внешнем запоминающем устройстве, а массив индекса может быть полностью размещен в оперативной памяти ЭВМ.

Если ключи записей, информация о которых выносится в индекс, приближенно образуют арифметическую прогрессию, мы получаем ситуацию с адресной функцией для индекса (рандомизация индекса).

Точное описание рандомизированного индекса состоит в следующем. Индекс с номером n хранит адрес записи основного массива, ключ которой равен или непосредственно больше значения

p (1)+z (n-1),

где z - константа (шаг арифметической прогрессии);

р (1) - значение ключа первой записи основного массива.

На рис. 6.4 показаны ключевые атрибуты основного массива (идентичные с предыдущим примером) и состояние массива рандомизированных индексов для z = 10. Примечательно, что значения ключей в таком индексе хранить не нужно.

Рассмотрим поиск с использованием рандомизированных индексов. На первой стадии номер требуемого далее индекса определяется по формуле

Результат деления округляется в меньшую сторону. Интервал записей основного массива на второй стадии поиска определяется адресами, указанными в n-м и (n+1)-м индексах.

Рис. 6.4. Рандомизация индекса

Важной разновидностью доступа к данным, которая требует специальных методов ускорения доступа, является обработка информации по нескольким ключевым признакам. В структуре записи массива определяется несколько ключевых атрибутов, причем в различных прикладных программах требуется доступ к записям по различным сочетаниям этих атрибутов и, возможно, требуется последовательная обработка всего массива.

Среди ключевых атрибутов записи устанавливается порядок старшинства. Извлекаемые на обработку записи должны быть упорядочены в пределах всего массива по самому старшему ключу. В пределах группы записей с одинаковым значением старшего ключа должна соблюдаться упорядоченность по значениям следующего по старшинству ключа и т. д. Проще всего представить упорядоченность по нескольким ключам с помощью следующей схемы.