1. Двухфазная задача вытеснения без учета капиллярных сил описывается моделью

Модель Баклея  Леверетта

Без учета капиллярных сил двухфазная фильтрация для случая прямолинейно-параллельного вытеснения рассматривалась С. Баклеем и М. Левереттом в 1942 г., а позже независимо от них А. М. Пирвердяном, исследовавшим также случай более общего закона фильтрации при двухфазном течении. Задачи двухфазной фильтрации без учета капиллярных сил известны как задачи (модель) Баклея – Леверетта. Задачи вытеснения такого типа в одномерной постановке изучены достаточно полно.

Уравнение насыщенности задач данного типа принадлежит к классу квазилинейных гиперболических уравнений первого порядка.

2. Сумма насыщенностей

Насыщенностью _i порового пространства i –й фазой называется доля объема пор V_i , занятая этой фазой в элементарном объеме:

, i=1,2,…, n где n – число фаз.

Очевидно, что .

3. В стационарно-реологической жидкости напряжение сдвига зависит

Касательное напряжение зависит только от градиента скорости

4. Сумма относительных проницаемостей

, 0<<1.

5. В вязкоупругой жидкости напряжение сдвига зависит

Для таких сред зависимость между касательными напряжениями и градиентом скорости более сложная; она включает производные по времени как напряжений, так и градиента скорости.

6. В нестационарно-реологической жидкости напряжение сдвига зависит

Cвязь между  и du/dy зависит от времени действия напряжений.

7. С ростом насыщенности расход фазы

Растет

Экспериментально установлено, что расход каждой фазы растет с увеличением перепада давления и насыщенности данной фазой.

8. Какие законы положены в основу расчета по методу Борисова

Законы Ома и Кирхгоффа

9. При расчете скважин, эксплуатирующих при нелинейной фильтрации, в методе Борисова необходимо добавить добавочное сопротивление к

10. На какой аналогии основан метод Борисова?

Электро–магнитной

Метод основанный на электро–магнитной аналогии и позволяющий сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки – к одиночно работающей скважине и к одиночно работающей батареи.

11. Метод Борисова позволяет рассчитать

а) приток к отдельной скважине

б) приток к батареи скважин

Методом Борисова позволяет сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки – к одиночно работающей скважине и к одиночно работающей батареи.

12. Второй закон Кирхгоффа

Алгебраическая сумма произведения дебитов на сопротивления равна алгебраической сумме потенциалов, действующих в замкнутом контуре.

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура.

13. Для уменьшения эффекта взаимодействия разбуривание надо вести в направлении

Уменьшения проницаемости пласта

Ослабление взаимодействия наблюдается в случае более низкой проницаемости в направлении линии расстановки скважин по сравнению с проницаемостью в перпендикулярном направлении.

14. Для параллельных сопротивлений общее сопротивление r равно

15. Для последовательных сопротивлений общее сопротивление r равно

16. Параметром уравнения пьезопроводности для упругой жидкости является

Коэффициент упругоёмкости пласта

Коэффициент упругоёмкости пласта – показывает долю объема жидкости от выделенного элемента объема пласта, высвобождающейся из элемента пласта при снижении давления на единицу. (^*=m₀_f +_c) [1/Па].

17. Упругий запас характеризует количество жидкости высвобождённой за счёт упругих свойств пласта при снижении

Давления

По Щелкачеву упругий запас – это количество жидкости, высвобождающейся в процессе отбора из некоторой области пласта при снижении пластового давления до заданной величины.

18. Степень нестационарности процесса определяет параметр

Фурье

Степень нестационарности процессов определяется безразмерными параметрами Фурье:

для призабойной зоны  ; для всего пласта –

19. Дилатантные жидкости характеризуются

Показательной функцией градиента скорости с n>1

Дилатантные жидкости - это такие материалы, у которых вязкость возрастает при увеличении скорости деформации сдвига. Такие жидкости являются одним из видов неньютоновских жидкостей.

20. Вязкопластичные жидкости характеризуются

Начальным сопротивлением сдвига

Для вязкопластичных жидкостей характерной особенностью является то, что они до достижения некоторого критического внутреннего напряжения т0 ведут себя как твёрдые тела и лишь при превышении внут­реннего напряжения выше критической величины начинают двигаться как обычные жид­кости.

21.Анизотропные тела характеризуются

(зависимостью изменения проницаемости от направления и зависимостью изменения пористости от направления)

22. Задача двухфазного вытеснения с учетом капиллярного давления описывается моделью (Рапопорта-Лиса) – подробно рассмотрено в 28.

23. Параметром уравнения пьезопроводности для газа является

функция Лейбензона

24. Капиллярное давление равно

Давления в фазах р₁ и р₂ не равны друг другу из-за капиллярных эффектов, приводящих к скачку давления на границе раздела фаз:

р₂-р₁=р_к ,

где р_к – капиллярное давление (или капиллярный скачок).

25. На границе двух фаз давление

Больше в менее смачиваемой фазе и меньше в более смачиваемой фазе

26. Псевдопластичная модель применима для описания течения

Для описания движения растворов и расплавов полимеров

27. Задача Баклея-Леверетта позволяет определить

Пренибрегаем капиллярным давлением, функция Баклея  Леверетта или функция распределения потоков фаз f() представляет собой отношение скорости фильтрации вытесняющей фазы к суммарной скорости, и равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз.

Функция Баклея – Лаверетта определяет полноту вытеснения и характер распределения нефтегазоконденсатонасыщенности по пласту.

28. Задача Раппопорта-Лиса позволяет определить

С учетом капиллярного скачка давления р_к, Модель Рапопорта – Лиса позволяет определить ширину данной зоны l и распределение насыщенностей по ней. В зоне l распределение насыщенности при постоянной скорости вытеснения – стационарно.

29. К стационарно реологическим жидкостям не относятся

Вязкоупругие – среды, обладающие свойствами как твердого тела, так и жидкости, а также способные к частичному восстановлению формы после снятия напряжений.

30. Внутренне фильтрационное сопротивление – это

Местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам. Появление этого сопротивления объясняется искривлением линий тока у скважин и, по Борисову, оно получило название внутреннего

( –- расстояние между скважинами батареи; h – толщина пласта, n – количество скважин)

31. Модель дилатантной жидкости применима для описания течения

Cуспензий с большим содержанием твердой фазы

32. Обратные активные задачи

Это задачи управления, регулирования процесса разработки пласта или месторождения.

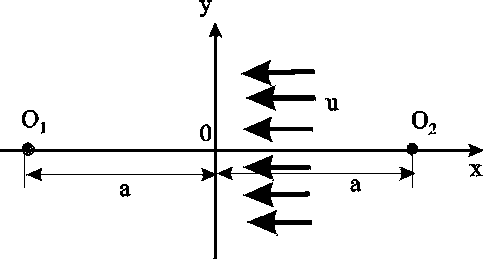
33. Решение задачи о притоке к скважине в пласте прямолинейным контуром питания требует

Определения поля течения. Для этого добиваются выполнения граничных условий на контуре. Затем вводят понятие, фиктивного источника О₂ с дебитом, равным дебиту стока О₁, путём зеркального отображения данного стока относительно прямой 0у.

34. Поле плоско-радиального течения характеризуется

Траектории всех частиц жидкости – прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют цилиндрические окружности с осью, совпадающей с осью скважины. (Горизонтальный пласт постоянной толщины h и неограниченной протяженности, подошва и кровля пласта непроницаемы. Пласт вскрыт единственной гидродинамически совершенной скважиной, то есть вскрыт на всю толщину, и забой полностью открыт. Для эксплуатационной скважины поток – радиально-сходящийся, а для нагнетательной – радиально-расходящийся. Плоскорадиальным потоком будет занята вся зона от стенки скважины до контура питания.