Лабораторная работа 2

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ РАДИОТЕХНИКИ,

ЭЛЕКТРОНИКИ И АВТОМАТИКИ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ

(СТАТИСТИЧЕСКАЯ РАДИОТЕХНИКА)

Лабораторная работа №2

«Исследование функций корреляции случайных процессов»

1. Содержание работы

1. Ознакомление с понятием функции корреляции случайных и детерминированных процессов.

2. Изучение связи функции корреляции с энергетическим спектром случайного процесса.

3. Экспериментальное измерение функции корреляции эргодических случайных процессов.

2. Теоретические сведения

Наиболее полно случайный процесс характеризуется многомерными плотностями вероятностей. Но в ряде случаев оказывается достаточным знание лишь отдельных параметров плотности вероятностей, так называемых – моментов.

Начальным моментом первого порядка или математическим ожиданием непрерывной случайной величины называется среднее значение случайной величины в сечении по ансамблю реализаций:

Второй начальный момент случайной величины равен среднему по ансамблю реализаций от квадрата этой случайной величины:

Обычно оперируют с центрированными случайными процессами , не содержащими статистического среднего, т.е.

Моменты центрированного случайного процесса называются центральными моментами.

Очевидно, для любой центрированной случайной величины центральный момент первого порядка равен 0. Второй центральный момент называется дисперсией случайной величины и определяется как математическое ожидание квадрата соответствующей центрированной величины:

Дисперсия характеризует рассеивание, разброс значений случайной величины около её математического ожидания и имеет размерность квадрата случайной величины.

В качестве характеристик случайной величины чаще всего используют первый начальный момент (математическое ожидание) и второй центральный момент (дисперсию).

Для стационарных случайных процессов первые и вторые моменты не зависят от времени.

Для эргодических случайных процессов усреднение по ансамблю может быть заменено усреднением по времени, т.е.

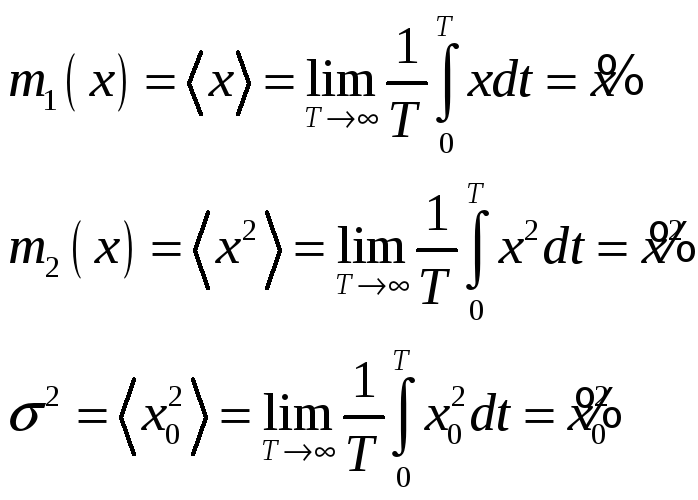
При этом временное среднее значение равно постоянной составляющей процесса. Дисперсия характеризует среднюю мощность переменной составляющей случайного процесса. Второй начальный момент характеризует суммарную мощность постоянной и переменной составляющих случайного процесса. Среднее значение (математическое ожидание) и дисперсия характеризуют случайный процесс статически, т.е. не дают сведения о его динамике, не позволяя тем самым прогнозировать поведение случайного процесса на некоторый интервал времени.

Зная значение процесса в момент времени , можно с определённой точностью спрогнозировать его значение в некоторый другой момент . Необходимые сведения о динамике случайного процесса даёт смешанная моментная функция второго порядка:

Она характеризует статистическую связь между мгновенными значениями случайного процесса в два различных момента времени и . Чем ближе расположены точки отсчётов и (или) медленнее процесс, тем большее количество реализаций будет характеризоваться одним знаком значений исследуемого процесса в точках отсчёта. По мере увеличения временного сдвига между отсчётами и (или) скорости изменения процесса процент таких реализаций будет меньше и значение уменьшится.

Если случайный процесс центрированный, то смешанная моментная функция второго порядка – корреляционная функция - определяется как математическое ожидание от произведения значений соответствующих центрированных функций, взятых в моменты времени и :

Здесь и - значения центрированных случайных функций в моменты времени и , соответственно:

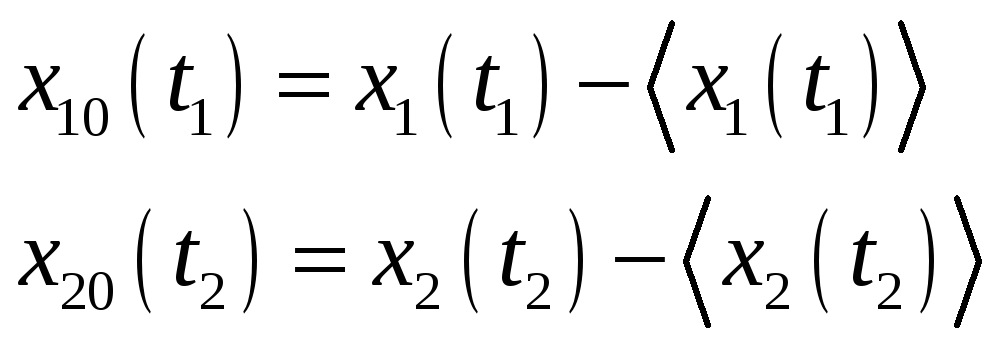
- двумерная плотность вероятностей случайного процесса .

Для стационарных случайных процессов двумерная плотность вероятностей зависит лишь от разности моментов отсчёта времени .

Поэтому и функция корреляции определяется усреднением по ансамблю реализаций произведения выборок и сдвинутых на .

Для эргодических случайных процессов функция корреляции определяется усреднением по времени произведения выборок из одной реализации, сдвинутых на интервал :

Корреляционная функция обладает следующими свойствами:

1. - функция корреляции стационарного случайного процесса является чётной функцией своего аргумента.

2. - функция корреляции при принимает максимальное значение, равное дисперсии.

3. Значение корреляционной функции чисто случайных процессов (не содержащих детерминированных составляющих) с ростом временного сдвига уменьшается . Корреляционная функция периодического сигнала не стремится к 0 при , что позволяет обнаружить периодический сигнал на фоне интенсивного шума.

4. Преобразование Фурье от функции корреляции должно быть неотрицательным, т.е. .

Для характеристики чисто временных связей используют нормированную функцию – коэффициент корреляции:

,

который в отличие от функции корреляции является безразмерной функцией, равной единице при и стремящейся к 0 при . При остальных значениях коэффициент корреляции не превышает по модулю единицы.

Значение , начиная с которого , называется интервалом корреляции. Величину определяют либо по уровню 0.05 функции , либо по формуле:

Различие между сигналами принято характеризовать взаимной корреляционной функцией, которая определяется по формуле:

Следует отметить, что перечисленные выше свойства относятся только к корреляционной функции и не справедливы для взаимной корреляционной функции .

Введём понятие спектра случайного процесса . Спектр случайных процессов является действительной функцией частоты и характеризует распределение мощности случайного процесса по частоте. Функция определяется как спектральная плотность мощности или энергетический спектр случайных процессов. Она является неотрицательной (), чётной функцией своего аргумента () и имеет размерность энергии .

Энергетический спектр и функция корреляции связаны между собой интегральным преобразованием Фурье (теорема Винера-Хинчина), т.е.

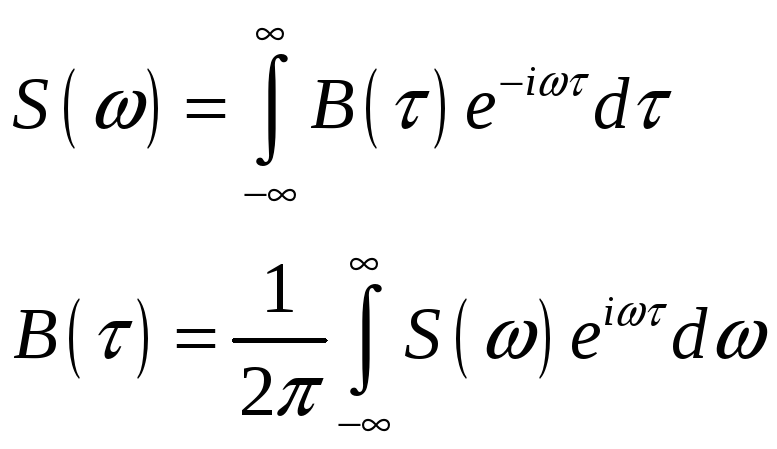
Из свойства преобразования Фурье следует, что ширина энергетического спектра и интервал корреляции обратнопропорциональны, т.е. .Следовательно, чем шире энергетический спектр случайного процесса тем меньше интервал корреляции и наоборот. «Белый шум» имеющий равномерный спектр во всей области частот, обладает функцией корреляции в виде дельта-функции.

3. Описание лабораторной установки

Экспериментальное определение функции корреляции основывается на использовании свойств эргодичности случайных процессов. При этом для отдельных реализаций имеем:

Согласно этой формуле, коррелятор должен состоять из линии задержки, перемножителя и интегратора. В качестве линии задержки использованы 6 последовательно соединённых линий с суммарной задержкой 4 мкс. Линия имеет отводы через каждые 0.2 мкс.

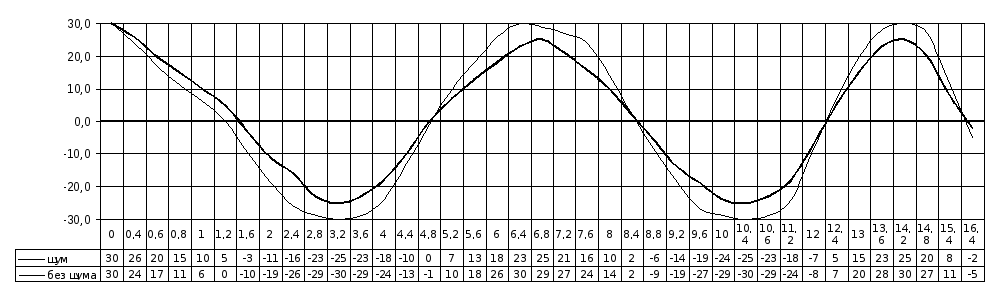
1. Зависимость напряжения на выходе коррелятора от величины задержки.

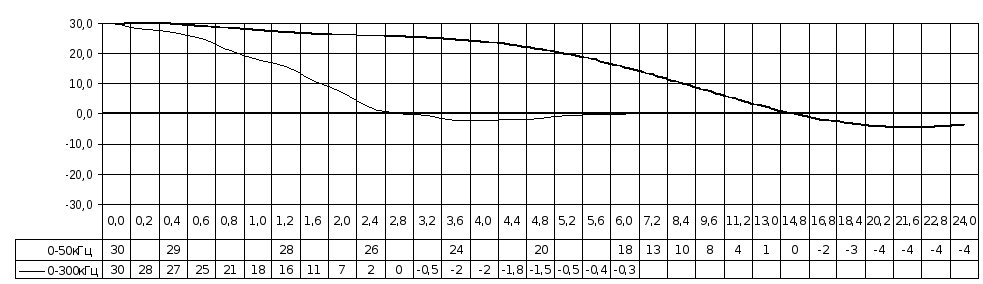
2. Зависимость напряжений на выходе коррелятора для двух значений напряжения шума.

0