
4.7 Диодные преобразователи частоты
Два варианта схем диодных ПЧ – на рис.4.24. На СВЧ схемы следует рассматривать как электрические эквиваленты, так как в реальных конструкциях СВЧ резонансные цепи выполняются в виде отрезков полосковых (микрополосковых) или коаксиальных линий и волноводов. Напряжение (мощность) от гетеродина подается на тот же колебательный контур, на который подается и сигнал (рис. 4.24,а) в том случае, когда частотаfГ, отличающаяся отfСна величину промежуточной частоты fПР, оказывается в полосе пропускания входного контура.
Если ослабление колебаний гетеродина во входном контуре слишком велико, то источники напряжений гетеродина и сигнала можно соединить в цепи диода последовательно – рис.4.24, б).
|
|
|
Р |
|
Рис. 4.25 –
Эквивалентные схемы диода
|
Эквивалентная схема диода – рис.4.25, а): g – активная проводимость;C– емкостьp-n-перехода;LS– индуктивность; rS– сопротивление соединительных проводников;CД– емкость держателя кристалла. На рис.4.25, б):C =Cpn+CД, где Cpn – емкостьp-n-перехода. |
У диодов, предназначенных для преобразования частоты в диапазонах дециметровых и сантиметровых волн, LS иrSочень малы. Их можно не учитывать и пользоваться более простой схемой – рис. 4.25,б):C– емкость диода, равная сумме емкостиp-n-перехода и емкости держателя кристаллаCД.
При анализе диодного ПЧ, как и ранее, будем полагать UГиUПРмалыми по сравнению сUГ.Это допущение соответствует истинному положению, так как для преобразования частоты напряжение гетеродина должно быть большим, чтобы изменение тока захватывало значительный нелинейный участок характеристики диода.
|
Р преобразователя частоты |
При малых уровнях преобразуемого сигнала и промежуточной частоты нелинейность диода не проявляется. При наличии модулирующего напряжения гетеродина диод для сигнала действует как линейная цепь с переменными параметрами и эквивалентную схему ПЧ – на рис. 4.26. |
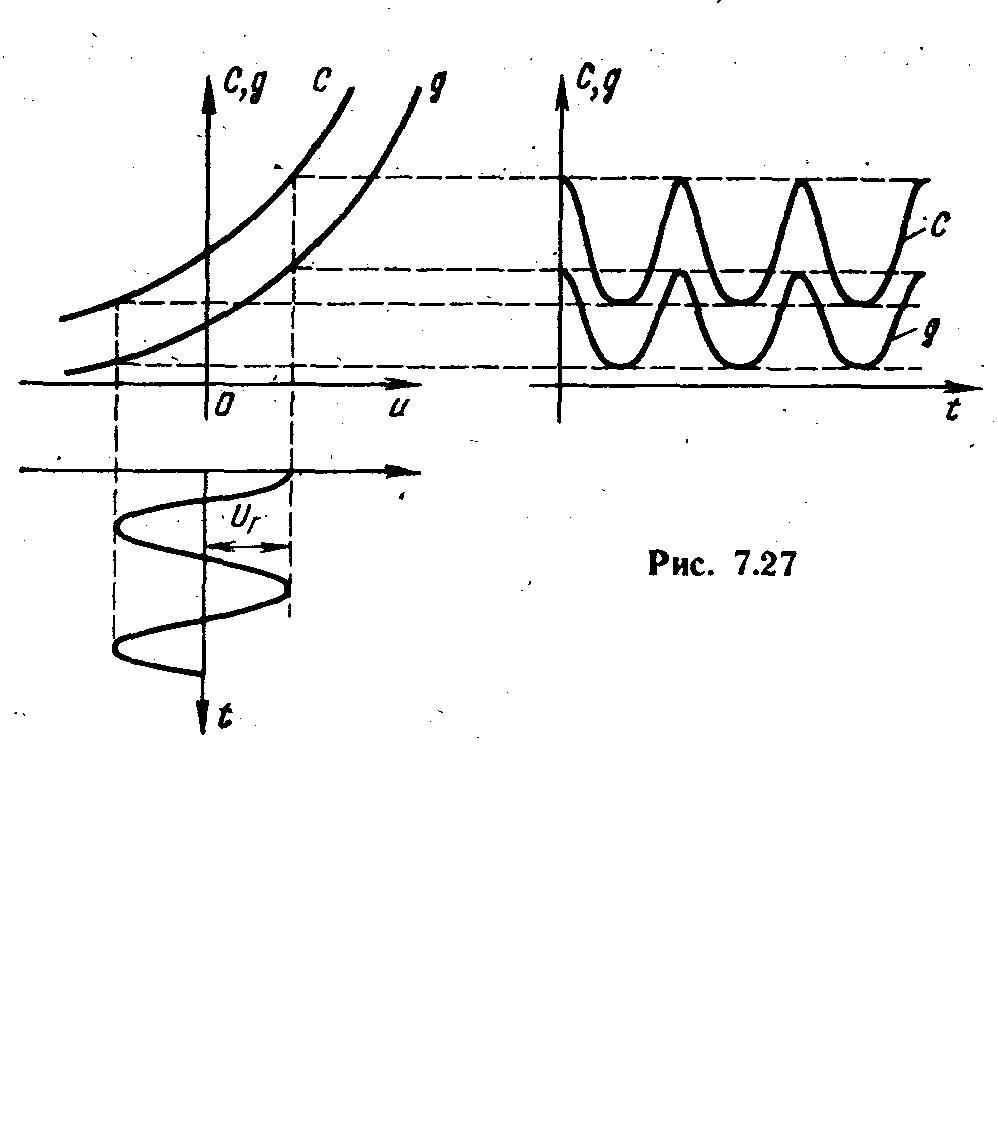
Изменение проводимости gи емкостиCдиода (рис. 4.27) под действием напряжения гетеродинаuГ = UГ cos(Гt)можно представить рядами Фурье:
g(t)
=
![]() +
+![]() coskГt;
C(t)
= C0 +
coskГt;
C(t)
= C0 +
![]() C0
coskГt. (4.33)
C0
coskГt. (4.33)
|
|
| |
|
|
Рис. 4.27 | |
Полный ток в цепи диода в соответствии со схемой рис.4.26
i = ug + dqС /dt,
где u = uС + uПР;qС — заряд емкости.
Учитывая равенство qС = Cu, определим ток в цепи диода:
i = ug + Cdu/dt + udC/dt. (4.34)
Напряжения сигнала uС и промежуточной частоты uПРопределяются выражениями (4.1) и (4.4). Фазовый уголПР зависит от соотношения емкостной и резистивной составляющих проводимостей диода и от фазового угла проводимости нагрузки (на рис.4.24 – резонансный контур). Подставляя в (4.34) значенияg(t)иC(t) из (4.33) иu = uС + uПР, заменяя произведения тригонометрических функций функциями суммарных и разностных углов и группируя слагаемые, можно получить выражение для тока диода.
Ток диода содержит составляющие различных частот. В случае не инвертирующего ПЧ ПР = kГ + C илиПР =C kГ, соответственноC= ПР ± kГ. Выделяя из суммы гармоник и комбинационных частот составляющие частотПР,C, находим токи iПР, iС.
Комплексные амплитуды токов частот ПР, C
İпр= 0,5ŪС (![]() +jПРCk)
+ ŪПР(
+jПРCk)
+ ŪПР(![]() +jПРC0),
+jПРC0),
İC=ŪС
(![]() +jCC0)
+ 0,5 ŪПР(
+jCC0)
+ 0,5 ŪПР(![]() +jCCk).
(4.36)
+jCCk).
(4.36)
Для инвертирующего ПЧ ПР = kГ C иC =kГ ПР.
Некоторые компоненты тока в цепи диода
в инвертирующем ПЧ имеют фазовые углы,
знак которых противоположен знаку
фазовых углов входных напряжений. Эти
компоненты обусловлены сопряженными
комплексными амплитудами напряжений
![]() и
и![]() .
Следовательно, у инвертирующего ПЧ
уравнения комплексных амплитуд токов
отличаются от (4.36):
.
Следовательно, у инвертирующего ПЧ
уравнения комплексных амплитуд токов
отличаются от (4.36):
İпр= 0,5 ŪС(![]() +jПРCk)
+ ŪПР(
+jПРCk)
+ ŪПР(![]() +jПРC0),
+jПРC0),
İC=ŪС(![]() +jCC0)
+ 0,5 ŪПР(
+jCC0)
+ 0,5 ŪПР(![]() +jCCk).
(4.37)
+jCCk).
(4.37)
Параметр СПР = 0,5Сkназываетсяпреобразующей емкостью;
Gпр=0,5![]() —
преобразующей проводимостьюили
крутизной преобразования.
—
преобразующей проводимостьюили
крутизной преобразования.
Введем обозначения для комплексных параметров преобразования:
Y11
=
![]() +
jCC0;
Y22
=
+
jCC0;
Y22
=
![]() +
jПРC0;
+
jПРC0;
Y12 = Gпр + jCCПР; Y21 = Gпр + jПРCПР. (4.38)
С учетом этих обозначений уравнения прямого и обратного преобразований для не инвертирующего диодного ПЧ (4.36) примут вид
İС=Y11 ŪС +Y12 ŪПР,İПР=Y21 ŪС +Y22 ŪПР, (4.39)
а уравнения прямого и обратного преобразований для инвертирующего диодного ПЧ (4.37) примут вид
İС=Y11 ŪС +Y12 ŪПР,İПР=Y21 ŪС +Y22 ŪПР. (4.40)
По форме (4.39) и (4.40) совпадают с (4.26), (4.27) и (2.23). Согласно (4.39) и (4.40) преобразующий элемент (ПЭ) можно представить в виде линейного четырехполюсника с Y-параметрами (4.38). Общая эквивалентная схема ПЧ с источником сигнала и нагрузкой приведена на рис.4.28.
|
Р |
Уравнения источника сигнала с входным контуром и нагрузки с учетом знака определяются выражениями
İС = m1İГ Y1 ŪС ; İПР = YНЭ ŪПР, (4.41); (4.42)
где Y1 =Yк1+m12YГ — суммарная проводимость входного контура и источника сигнала, пересчитанная к контуру в точках 1–1;Yк1=Gк1+jВк1 – собственная проводимость входного контура;YНЭ =Yк2+m22YН – проводимость эквивалентной нагрузки ПЭ в точках 2–2;
Yк2 =Gк2+jВк2 – собственная проводимость выходного контура;İГ =ЕГYГв соответствии с теоремой об эквивалентном генераторе;ЕГ – ЭДС источника сигнала.
Коэффициент передачи напряжения ПЭ КП = ŪПР /ŪСнайдем, подставив в первое выражение (4.39) уравнение нагрузки (4.42), для не инвертирующего ПЧ
КП =Y21/YЭ2; (4.44)
для инвертирующего ПЧ
КП =Y21/YЭ2. (4.45)
Здесь YЭ2 =YНЭ+Y22 — эквивалентная проводимость выходного контура.
Используя вторые уравнения (4.39) и (4.40), можно определить входную проводимость в точках 1–1 преобразующего элемента ПЭ – рис. 4.28. С учетом (4.44) и (4.45) для неинвертирующего ПЧ
YВХ =İС/ŪС С=Y11+Y12 ŪПР /ŪС =Y11Y12 Y21/ YЭ2; (4.46)
для инвертирующего ПЧ
YВХ = Y11 + Y12 Y21/ YЭ2. (4.47)
Выходную проводимость ПЭ в точках 2–2 найдем из первого уравнения (4.39):
YВЫХ =İПР/ŪПР=Y22+Y21 ŪС /ŪПР. (4.48)
Здесь ŪС /ŪПР=КОБР– коэффициент передачи ПЭ при обратном преобразовании. Из (4.39) и (4.41) получим
КОБР= ŪС /ŪПР=Y12 / YЭ1, (4.50)
где YЭ1=Y1 +Y11– эквивалентная проводимость входного контура. При рассмотрении обратного преобразования полагаемЕГ= 0.
Подставляя (4.50) в (4.48), получаем для не инвертирующего ПЧ
YВЫХ =Y22Y12 Y21/ YЭ1. (4.51)

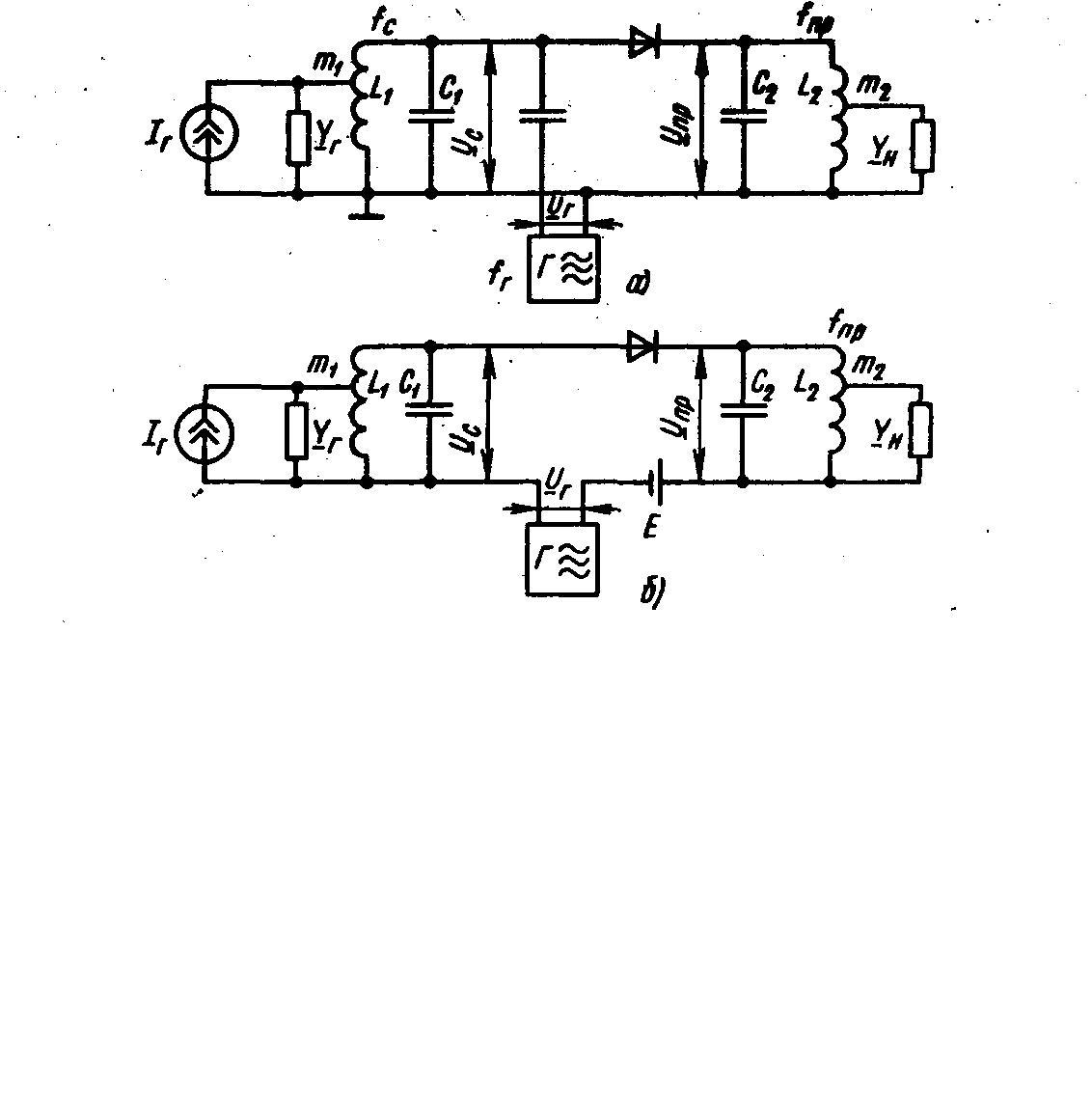
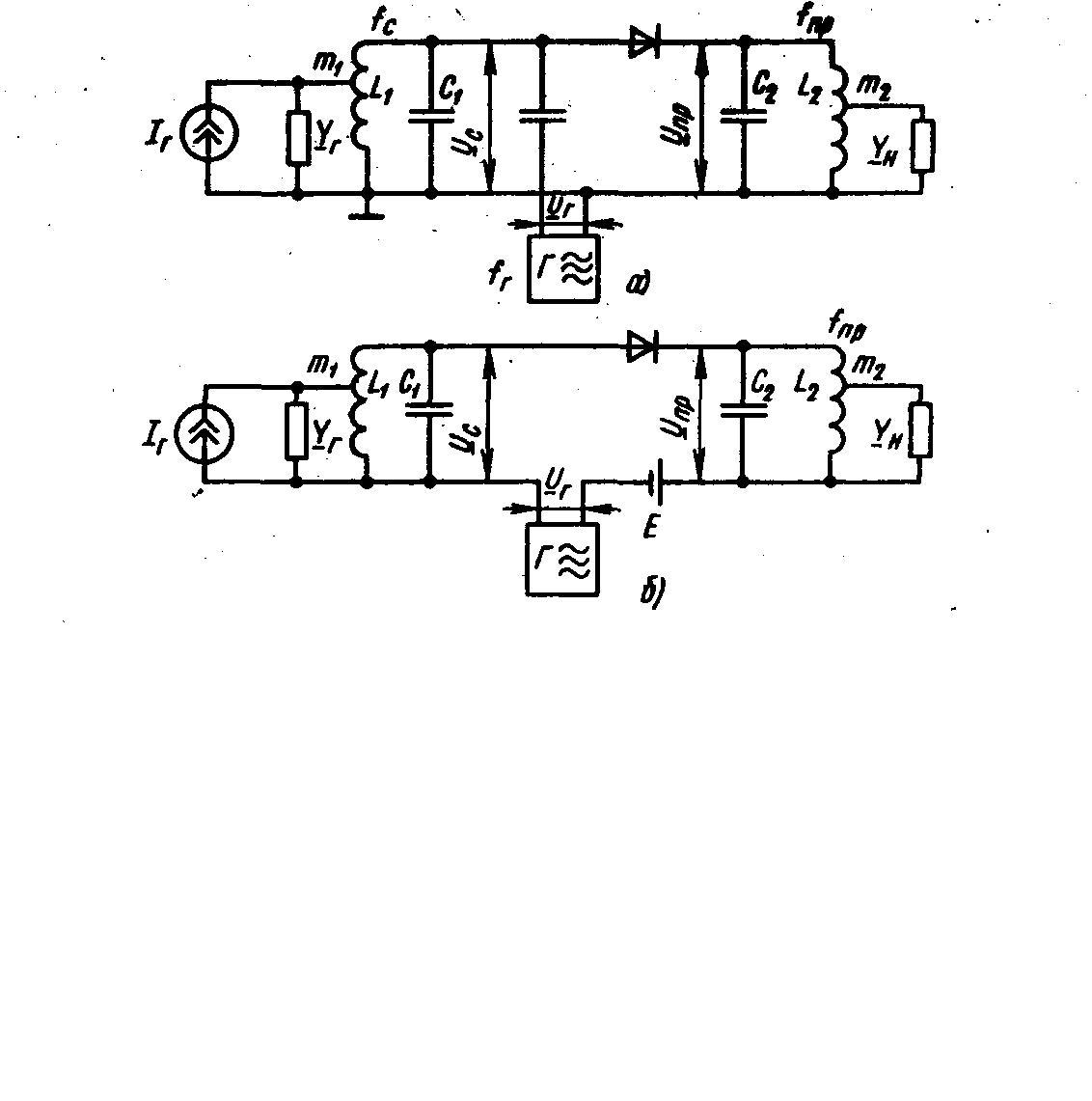 ис.4.24
– Диодный преобразователь частоты
ис.4.24
– Диодный преобразователь частоты
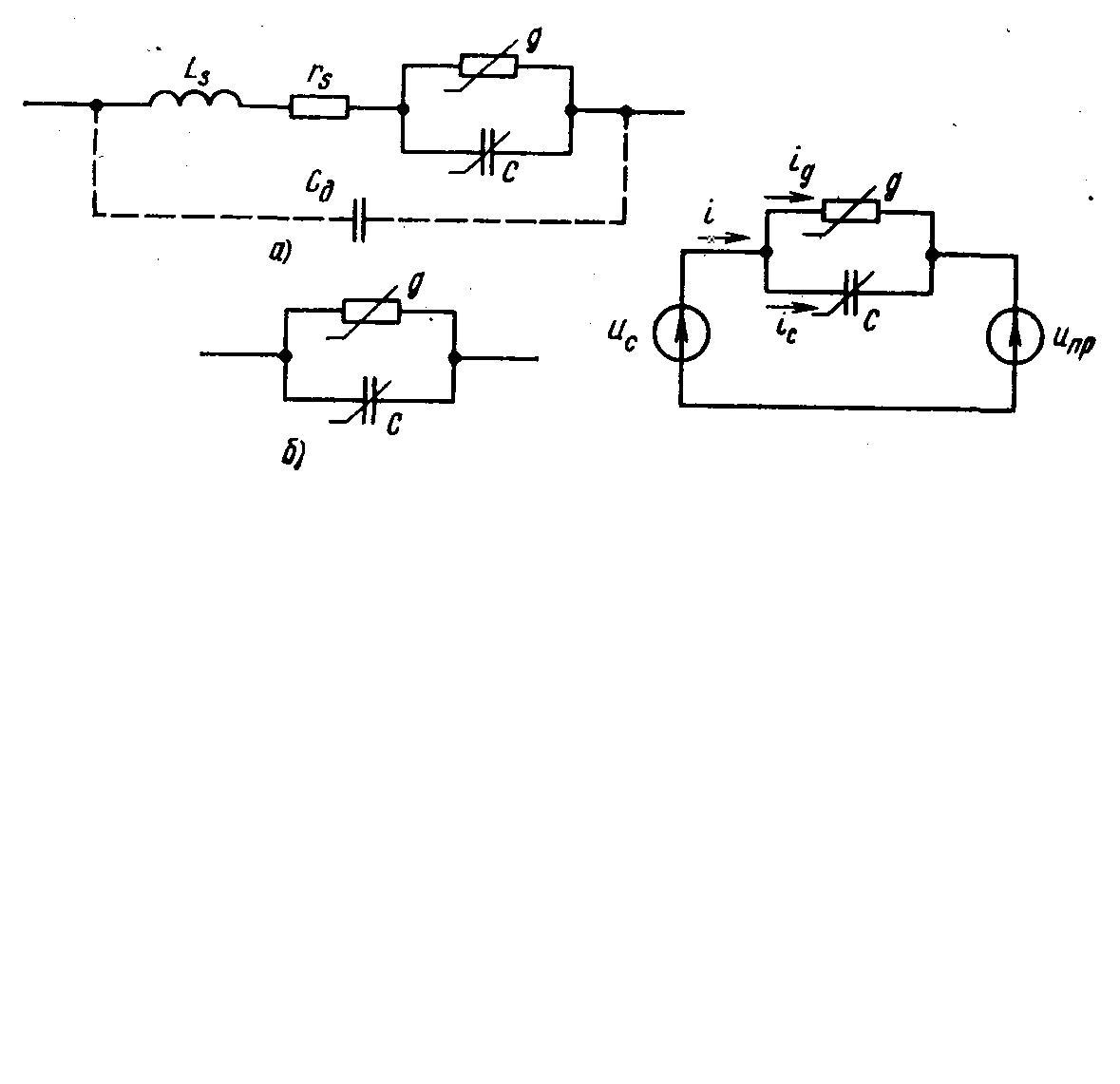
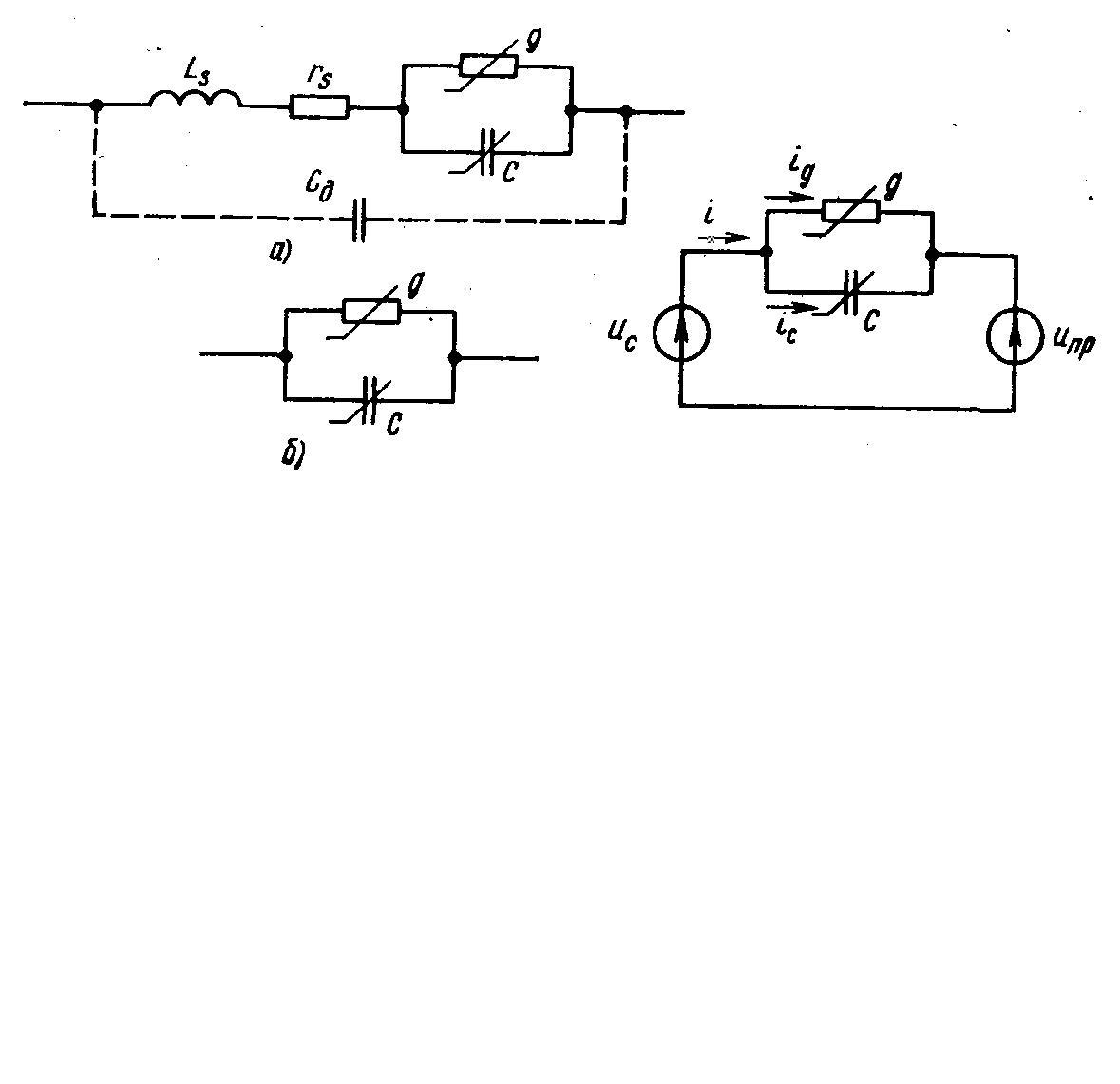 ис.
4.26 – Эквивалентная схема
ис.
4.26 – Эквивалентная схема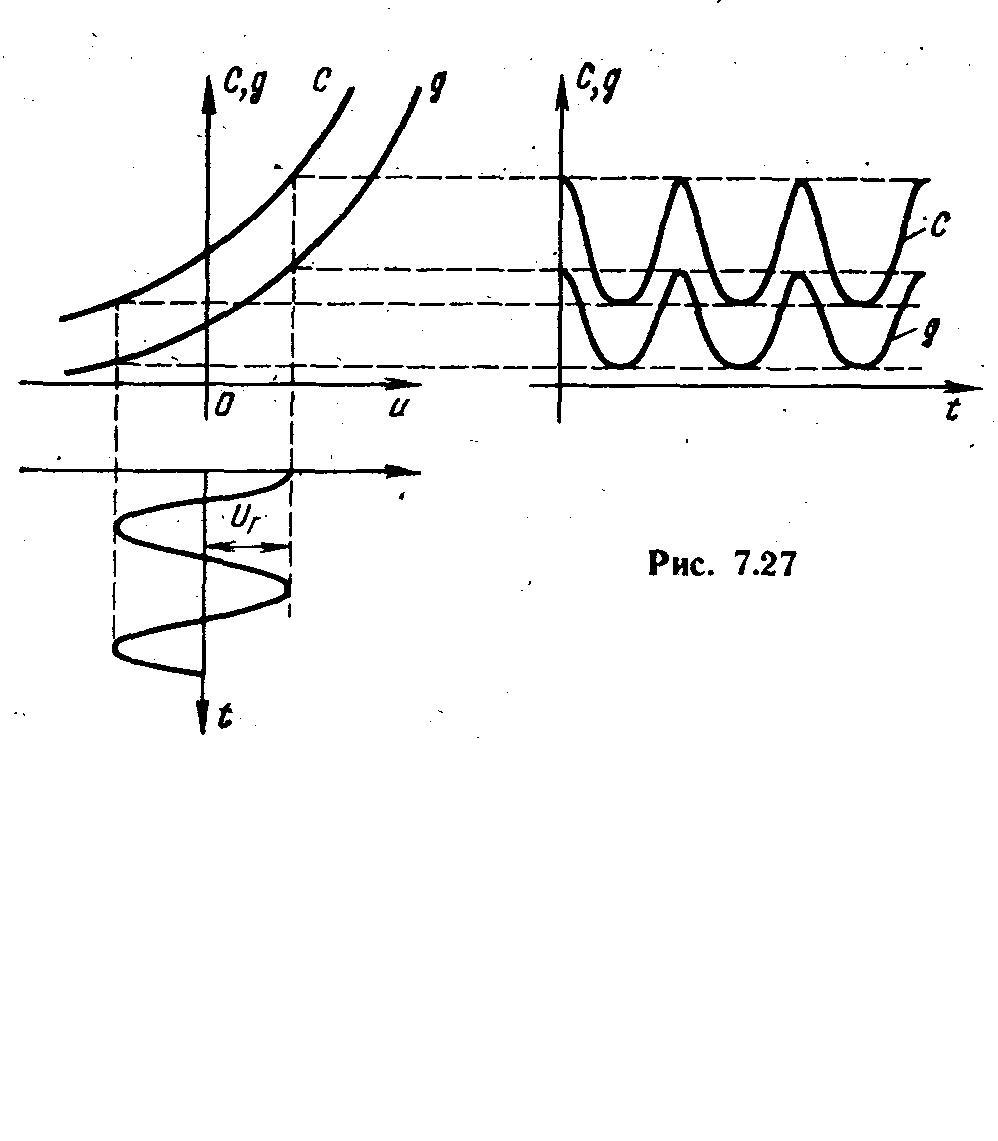
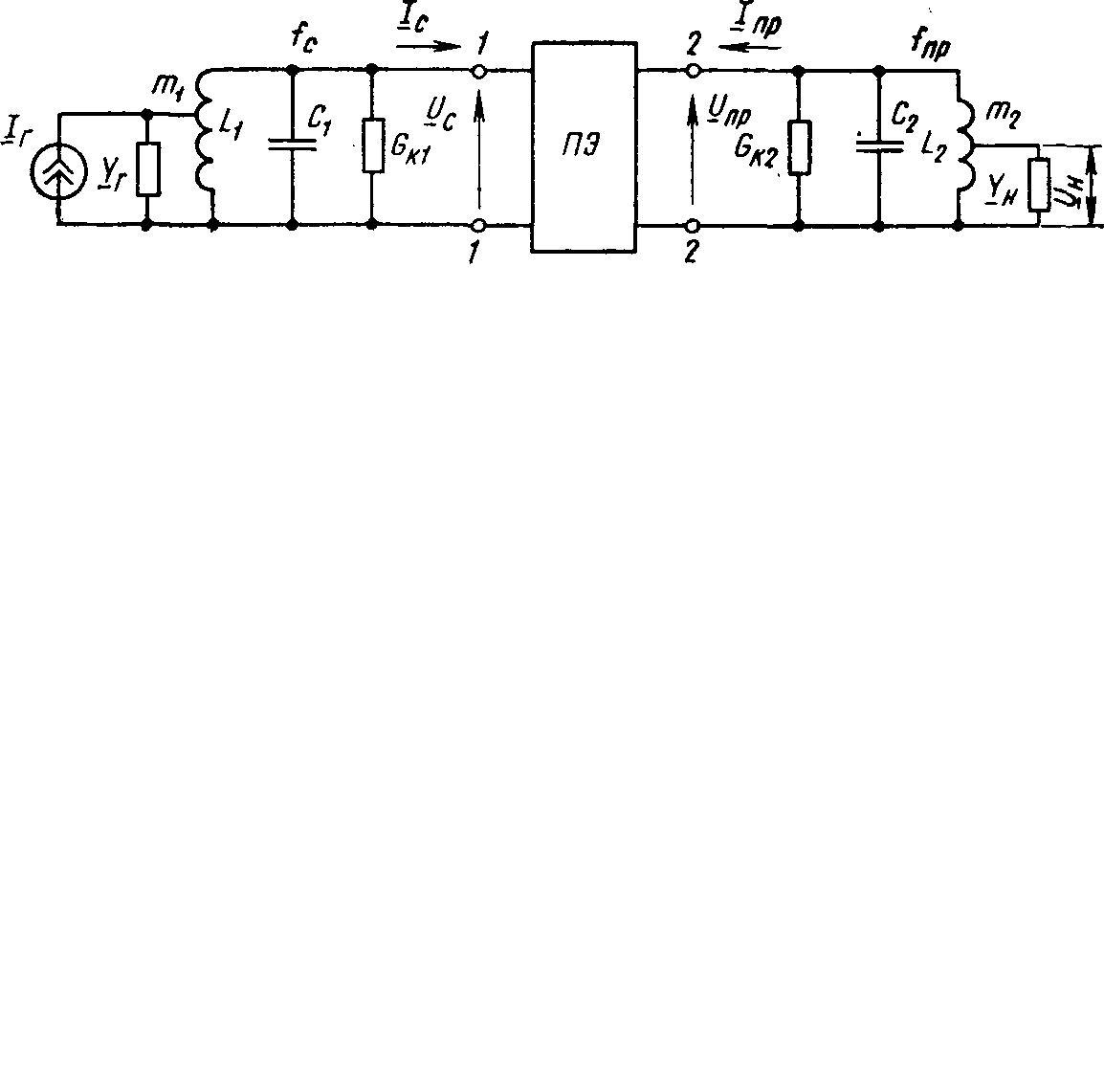 ис.4.28
– Эквивалентная схема преобразователя
частоты
ис.4.28
– Эквивалентная схема преобразователя
частоты