Импликация
Результатом операции импликации для высказывания А В будет ложь только тогда, когда первое высказывание (А) истинно, а второе (В) ложно. При этом А – предпосылка, а В – следствие.
Пример 15. Высказывания А = «2 + 2 = 4» и В = «1 – 8 = 5». Сложное высказывание А В (А В) ложно, так как высказывание А истинно, а В – ложно.
Антиконъюнкция
Результатом операции антиконъюнкции для высказывания А В будет ложь только тогда, когда оба высказывания истинны.
Пример 16. Высказывания А= «Москва – столица России» и В= «Рим – столица Италии». Сложное высказывание А В ложно, так как истинны оба высказывания.
Антидизъюнкция
Результатом операции антидизъюнкции для высказывания А В будет истинна только тогда, когда оба высказывания ложны.
Пример 17. Высказывания А= «Рим – столица России» и В= «Москва – столица Италии». Сложное высказывание А В истинно, так как ложны оба высказывания.
Основными символами алгебры логики являются:
пропозициональные переменные;
унарная связка и бинарные связки , , , ~;
скобки ( ).
Переменная, значениями которой являются высказывания, называется пропозициональной переменной.
Далее индуктивно вводится понятие формулы, являющееся формализацией понятия «сложного» высказывания. К формуле алгебры логики относят:
выражение, состоящее только из пропозициональной переменной (А1, В, с);
выражения, состоящие из пропозициональных формул соединенных связками ( С, (А1 А2), (Н1 Н2)).
Правила сокращения записей в пропозициональных формулах:
вместо А пишут ;
вместо А1 А2 пишут А1А2;
приоритет применения связок возрастает в следующем порядке
~
внешние скобки опускаются.
Пример 18.
;
.
Для преобразований формул в равные формулы важную роль в алгебре логики играют следующие равенства:
(закон коммутативности).
(закон ассоциативности).
(закон поглощения).
(закон дистрибутивности).
(закон противоречия).
(закон исключенного третьего);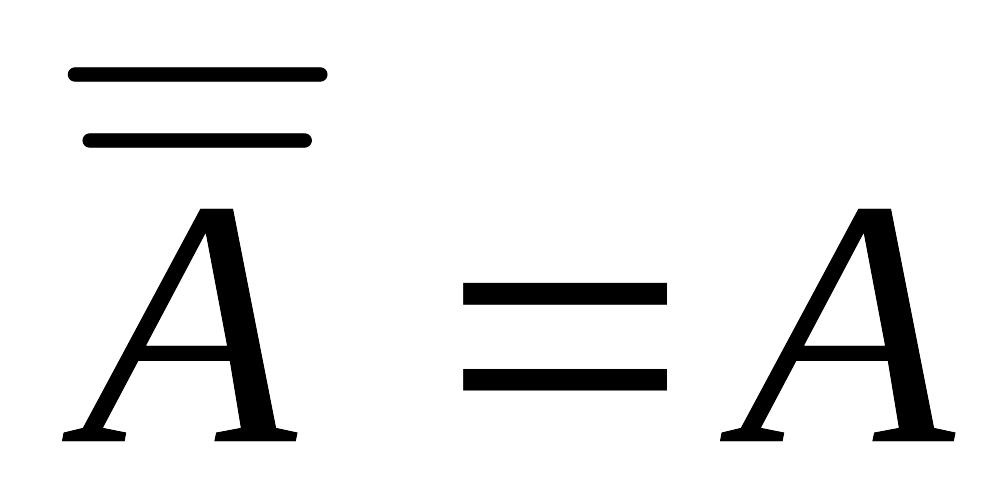
(закон снятия двойного отрицания);
(закон склеивания);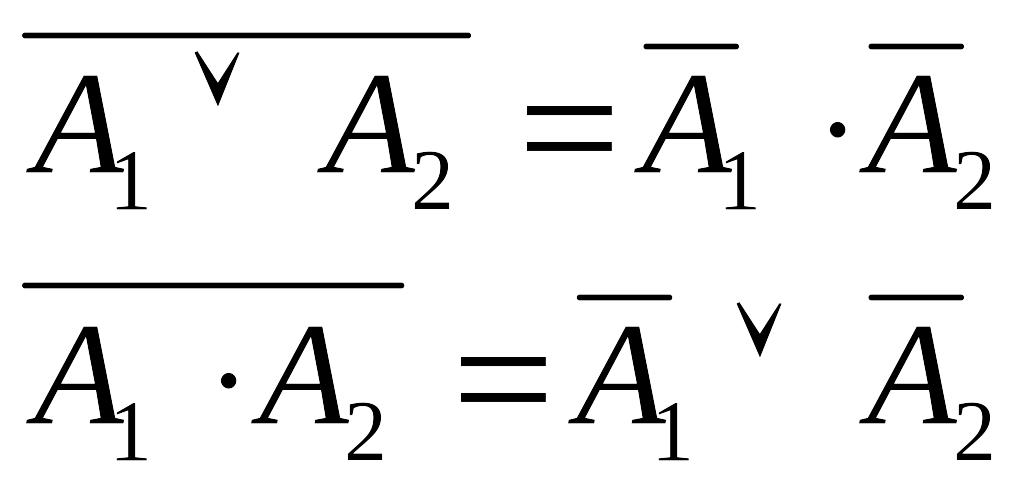
(закон де Моргана);
(закон свертки).
Эти равенства позволяют существенно упростить запись формул освобождением от лишних скобок.
2.2. Нормальные формы
Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые.
Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые.
Конъюнктивная нормальная форма
Всякая конъюнкция элементарных дизъюнкций называется конъюнктивной нормальной формой, то есть КНФ.
Совершенной КНФ (СКНФ) называется КНФ, в которой нет равных элементарных дизъюнкций и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с отрицанием).
Дизъюнктивная нормальная форма
Всякая дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой, то есть ДНФ.
Совершенной ДНФ (СДНФ) называется ДНФ, в которой нет равных элементарных конъюнкций и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с отрицанием).
3. Применение средств алгебры логики для описания функционирования устройств компьютера
Для описания того, как функционируют аппаратные средства компьютера очень удобен математический аппарат алгебры логики, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры «1» и «0».
Следовательно, одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных; на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Данные и команды в памяти компьютера и в регистрах процессора представляются в виде двоичных последовательностей различной структуры и длины.
Существуют различные физические способы кодирования двоичной информации, но чаще всего единица кодируется более высоким уровнем напряжения, чем ноль.
В логической схеме компьютера выделяют логические элементы. Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую формулу.
Логическими элементами компьютеров являются электронные схемы «И», «ИЛИ», «НЕ», «И-НЕ», «ИЛИ-НЕ» и другие (называемые также вентилями), а также триггер. С помощью этих схем можно реализовать любую логическую формулу, описывающую работу устройств компьютера.
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую формулу, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Схема «И» реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы «И» с двумя входами представлено на рис. 5.
Рис. 5. Схема «И»
На выходе схемы «И» значение «1» будет тогда и только тогда, когда на всех входах будут «1». Когда хотя бы на одном входе будет «0», на выходе также будет «0».
Операция конъюнкции на функциональных схемах обозначается знаком «&» (читается как «амперсэнд»), являющимся сокращенной записью английского слова and.
Схема «ИЛИ» реализует дизъюнкцию двух или более логических значений. Условное обозначение схемы «ИЛИ» представлено на рис. 6.
Рис. 6. Схема «ИЛИ»
Значение дизъюнкции равно «1», если сумма значений операндов больше или равна «1». Когда хотя бы на одном входе схемы «ИЛИ» будет «1», на её выходе также будет «1».
Операция дизъюнкции на функциональных схемах обозначается знаком «1».
Схема «НЕ» (инвертор) реализует операцию отрицания. Условное обозначение схемы НЕ представлено на рис. 7.
Рис. 7. Схема «НЕ»
Если на входе схемы – «0», то на выходе будет «1». Когда на входе – «1», на выходе будет «0».
Схема «И-НЕ» состоит из элемента «И» и инвертора и осуществляет отрицание результата схемы «И». Условное обозначение схемы «И-НЕ» представлено на рисунке 8. Таблица истинности схемы «И-НЕ» – это таблица 5.
Рис. 8. Схема «И-НЕ»
Таблица истинности схемы «И-НЕ»
Таблица 5
х |
у |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Схема «ИЛИ-НЕ» состоит из элемента «ИЛИ» и инвертора и осуществляет отрицание результата схемы «ИЛИ». Условное обозначение схемы «ИЛИ-НЕ» представлено на рис. 9, а таблица истинности схемы ИЛИ-НЕ – это табл. 6.
Рис. 9. Схема «ИЛИ-НЕ»
Таблица истинности схемы «ИЛИ-НЕ»
Таблица 6
х |
у |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
