1. Проекции с параллелями постоянной кривизны

• Параллели прямые линии. Описывается уравнениями, выраженными только в прямоугольной системе координат. Включает 4 класса проекций

1. Ц илиндрические проекции (меридианы - равностоящие параллельные прямые, а параллели – параллельные прямые, ортогональные меридианам). Их общие уравнения х=f(φ) и y=βλ

Где β – параметр проекции

2. о бобщенные цилиндрические проекции (меридианы – неравностоящие параллельние прямые, а параллели – параллельные прямые,ортогональные меридианам. Об. Ур-е х=f₁(φ) и х=f₂(λ)

3. Псевдоцилиндрические проекции (параллели – параллельные прямые, меридианы – кривые или прямые симметричные относительно среднего прямолинейного меридиана.

Об. Ур-я х=f₁(φ) и х=f₂(φ,λ)

4. цилиндрическо-конические проекции, в которых параллели изображаются пучком прямых, а меридианы – концентрическими окружностями.

• Конические окружности. Выражаются в системах плоских полярных и прямоугольных координат.

1. К 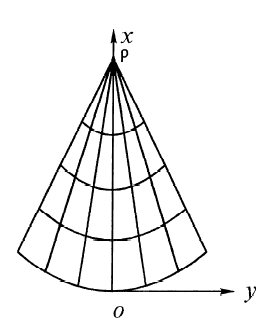онически епроекции (параллели – концентрические окружности, а меридианы – пучок прямых, исходящих из центра окружности). Углы между меридиаными на проекции δ пропорциональны углам между ними на поверхности эллипсоида (шара). В точке полюса Р имеется разрыв изображения. Ур-я

2. Обобщенные конические проекции (параллели – конц окружности, меридианы - пучок прямых, исходящих из центра окружности). Углы между меридиаными на проекции δ являются функциями этих углов на эллипсоиде (шаре). В точке полюса Р имеется разрыв.

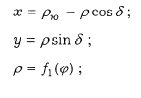
3. Псевдоконические проекции (параллели - концентрические окружности, меридианы – кривые симметричные относительно среднего прямолинейного меридиана). Уравнения

4. Азимутальные проекции (параллели -концентрические окружности, меридианы - пучок прямых, исходящих из центра окружности). В точке полюса отсутствует разрыв изображения. Углы между меридианами на проекции равны углам между ними на шаре (эллипсоиде). Плоские полярные координаты выражаются в функции полярных сфероидических (сферических) координат z=const, a=const. Уравнения

5. Обобщенные азимутальные проекции (параллели -концентрические окружности, меридианы - пучок прямых, исходящих из центра окружности, углы между ними являются функциями этих углов на эллипсоиде, в точке полюса отсутствует разрыв изображения. Меридианы с долготами 0 и 360 совпадают). Уравнения

6. Псевдоазимутальные проекции. Параллели – конц. Окр, в точке полюса нет разрыва изображения. Меридианы с долготами 0 и 360 совпадают и являются либо прямыми либо кривыми, в каждой точке которых они имеют одинаковую кривизну, остальные меридианы – прямые или кривые линии. Уравнения

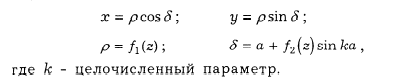
• Эксцентрические окружности. Выражаются в плоских и прямоугольных координатах.

1. Поликонические проекции в широком смысле(параллели – эксцентрические окружности, центры которых находятся на среднем меридиане, а меридианы – кривые симметричные относительно среднего прямолинейного меридиана). Уравнения

2. Поликонические проекции в узком смысле. Накладывается еще два условия: полярный радиус p=Nctg φ. Частный масштаб длин на среднем меридиане имеет постоянное значение m₀=k, в частности m₀=1.

2) Картографические проекции с параллелями переменной кривизны

• Полиазимутальные проекции и обобщенные полиазимутальные проекции

1. Полиазимутальные проекции. Параллели-эллипсы, меридианы – пучок прямых или кривых, исходящих из центра эллипсов, в точке полюса отсутствует разрыв изображения. Общие уравнения

2. Обобщенные полиазимутальные (параллели – кривые произвольной кривизны, а меридианы пучок прямых или кривых, исходящих из точки полюса, в котором нет разрыва изображения). Общие уравнения

• Обобщенные поликонические, различающиеся изображением параллелей; в виде – эллипсов, парабол, гипербол и параллелями произвольной кривизны, меридианы изображаются кривыми линиями. Обобщенные уравнения

• Полицилиндрические проекции. Параллели и меридианы изображаются кривыми произвольной или заданной кривизны (эллипсами, параболами и гиперболами)

Общие уравнения

• Проекции произвольных поверхностей, картографическая сетка которых отражает форму картографических поверхностей. Обобщение азимутальных, цилиндрических, конических и др проекций.

• Проекции для создания аноморфированных карт, обладающие дополнительными функциональными возможностями:

1. Варивалентные проекции

2. Переменно-масштабные проекции (при сохранении общего масштаба карты достигается сжатие или растяжение изображения на ее отдельных участках

3. Проекции с измененной метрикой пространства (исп эвклидова метрика и др метрики)

Классификация проекций По характеру искажений (свойствам изображения)

• Равноугольные (картографическая сетка ортогональна, частные масштабы длин не зависят от направлений, но имеются большие искажения площадей)

• Равновеликие (сохраняется постоянным отношение площадей на поверхности эллипсоида или плоскости, но имеются большие искажения углов)

• Произвольные (не выполняется ни равноугольность, ни равновеликость)

Классификация проекций по способам получения

• Решение прямой задачи математической картографии. Определяются отображающие функции, с их использованием получают формулы для вычисления частных масштабов длин, площадей и др характеристик проекции.

• Решение обратной задачи математической картографии осуществляется по заданным значениям характеристик проекции. Определяются прямоугольные координаты искомой проекции и недостающие ее характеристики.