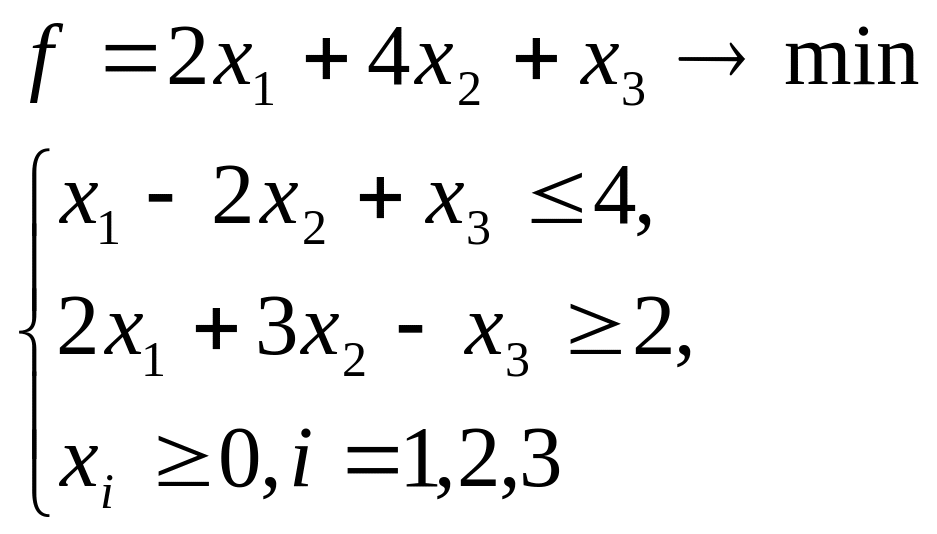Объективно обусловленные оценки и их смысл.

Компоненты оптимального решения двойственной задачи называются оптимальными (двойственными или объективно обусловленными) оценками исходной задачи.

Таблица 7

число единиц продукции		остатки ресурсов
p1	p2	S1	S2	S3	S4
x1=6	x2=4	x3=0	x4=0	x5=1	x6=3
y5=0	y6=0	y1=4/5	y2=3/5	y3=0	y4=0
превышение затрат на ресурсы над ценой ресурса		объективно обусловленные оценки ресурсов (условные цены ресурсов)

Объективно обусловленные оценки ресурсов определяют степень дефицитности ресурсов по оптимальному плану производства. У дефицитных ресурсов объективно обусловленная оценка отлична от нуля, у недефицитных равна нулю. В нашем случаи ресурсы S₁ и S₂ расходуются полностью, т.е. являются дефицитными, а ресурсы S₃ и S₄ носят избыточный характер, т.е. в данном производственном цикле полностью не расходуются.

Рассмотрим превышение затрат на ресурсы над ценой ресурса. Если бы, например, y₆>0, то х₂=0, и из этого следовало бы, что продукцию Р₂ производить не выгодно, т.к. затраты на ресурсы превысили бы цену изготовляемой из них продукции. Следовательно в оптимальный план производства могут попасть только рентабельные, неубыточные виды продукции.

Третья теорема двойственности: компоненты оптимального решения двойственной задачи равны значениям частных производных функции F_max(b₁,b₂,…b_m) по соответствующим аргументам

Двойственные оценки могут служить инструментом анализа и принятия правильных решений в условиях постоянно меняющегося производства. Так, например, с помощью объективно обусловленных оценок ресурсов возможно сопоставление оптимальных условий затрат и результатов производства.

Пример 10.

В результате решения задачи был получен оптимальный план Р₁ и Р₂. Появилась возможность выпуска продукции Р₃. Затраты каждого ресурса S₁, S₂, S₃ и S₄ на выпуск этой продукции соответственно равны: a₁₃=3, a₂₃=2, a₃₃=4 и а₄₃=1. Цена продукции с₃=3. Даст ли прибыль включение в план дополнительной продукции?

X^*=(6;4;0;0;1;3) и Y^*=(4/5;3/5;0;0;0;0).

Сопоставим дополнительные затраты на ресурсы в расчете на единицу продукции Р₃ с ценой ее реализации:

a₁₃y₁^*+a₂₃y₂^*+a₃₃y₃^*+a₄₃y₄^*=3*4/5+2*3/5+4*0+1*0=3.6

Полученный результат больше, чем цена продукции с₃=3, следовательно ее выпуск не является рентабельным. Ясно, чтобы включение новой продукции в производство было выгодно, надо, чтобы ее цена мыла не менее 3,6.

Объективно обусловленные оценки ресурсов позволяют судить об эффекте не любых, а лишь сравнительно маленьких изменениях ресурсов. При крупных изменениях меняются сами оценки, что делает невозможным использование оценок для анализа производства.

Задания.

1. Постройте задачи, двойственные к данным:

   1. 

   2. 

   3. 

   4. 

   5. 

2. Постройте задачу, двойственную к данной. Решите прямую и двойственную задачу графическим методом:

   1. 

   2.