Задания.

Задачи 1-6 из раздела особые случаи симплекс-метода решить с помощью М-метода.

Двойственные задачи

Экономическая интерпретация двойственной задачи.

Рассмотрим две задачи ЛП

Таблица 4

Задача 1 (исходная)	Задача 2 (двойственная)
Целевая функция: F=c1x1+ c2x2+…+ cnxnmax При ограничениях И условиях неотрицательности x10, x20,… xn0 Составить такой план выпуска продукции Х=(х1, х2,…хn), при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов	Целевая функция: Z=b1y1+ b2y2+…+ bnynmax При ограничениях И условиях неотрицательности y10, y20,… ym0 Найти такой набор цен (оценок) ресурсов Y=(y1, y2,…yn), при котором общие затраты на ресурсы будут минимальны при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли от реализации этой продукции

Цены ресурсов y₁, y₂…y_m - это цены на ресурсы, которые мы называем учетными, неявными, теневыми. Смысл этих названий состоит в том, что это условные "ненастоящие" цены, которые появились бы в том случае, если фирма, осуществляющая данный производственный процесс, вместо производства, решила бы продать имеющиеся ресурсы, причем таким образом, чтобы прибыль от их продажи была бы не меньше, чем прибыль от данного производственного процесса. А фирма, покупающая ресурсы, желала бы минимизировать затраты на покупку. В отличие от "внешних" цен с₁, с₂…с_n на продукцию, известных до начала производства, цены ресурсов y₁, y₂…y_m считаются "внутренними", не известными до начала производственного процесса, так как они определяются в процессе решения задачи. Их называют оценками ресурсов.

Свойства взаимно двойственных задач.

1. В одной задачи ищется максимум, в другой минимум линейной функции.

2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи.

3. Каждая задача записана в стандартной форме, причем в задаче на минимум все неравенства вида "", а в задаче на максимум - вида "".

4. Матрицы коэффициентов при переменных в системах ограничений обоих задач являются транспонированными друг к другу: А и А^т.

5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных другой задачи.

6. Условия неотрицательности переменных имеются в обеих задачах.

Две задачи ЛП, обладающие этими свойствами называются симметричными взаимно двойственными (двойственными).

Алгоритм составления двойственных задач.

1. Приводим все неравенства системы ограничений исходной задачи к одному символу (причем в задаче на минимум к "", а в задаче на максимум к "").

2. Составляем расширенную матрицу А₁, в которую включаем матрицу А, столбец свободных членов и строку переменных коэффициентов целевой функции.

3. Находим А₁^т.

4. Формулируем двойственную задачу на основе полученной матрицы А₁^т и условии неотрицательности переменных.

Пример 8.

Приведем ограничения к виду ""

Составим расширенную матрицу А₁

Транспонируем матрицу:

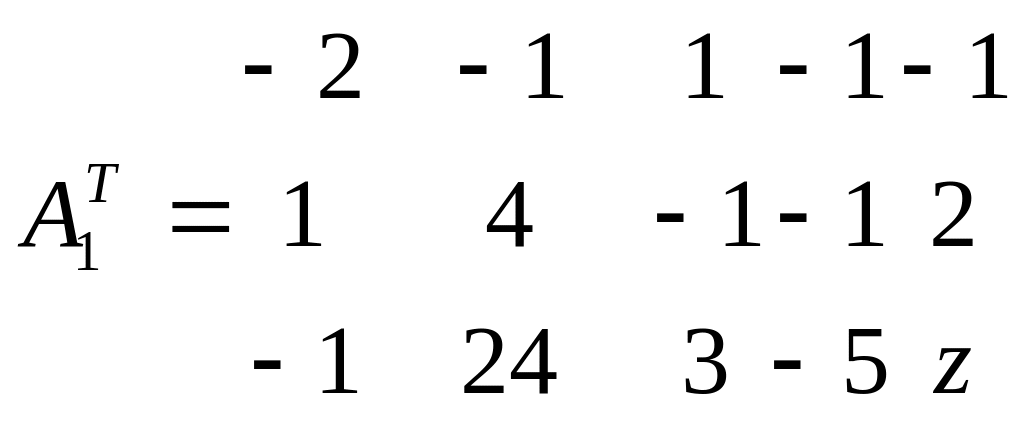
И сформулируем двойственную задачу:

Первая (основная) теорема двойственности: если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая задача, причем оптимальные значения их целевых функций равны. F_max=Z_min. Если область допустимых решений одной из задач неограниченна, то условия другой задачи противоречивы.

Замечание. Обратное утверждение не верно. Если условия одной задачи противоречивы, это не означает, что другая задача неограниченна.

Экономический смысл первой теоремы двойственности. План производства Х^*=(х^*₁, х₂^*,…х^*_n) и набор оценок ресурсов Y^*=(y^*₁, y₂^*,…y^*_m) оказываются оптимальными тогда и только тогда, когда прибыль от продукции, найденная по "внешним", заранее известным ценам с₁, с₂,…с_n, равна затратам на ресурсы по "внутренним", определенным в процессе решения, ценам y₁, y₂,…y_m. Для всех других планов Х и Y прибыль всегда меньше (или равна) затратам на ресурсы. Т.е. предприятию безразлично производить ли продукцию по оптимальному плану X^* или продавать ресурсы по оптимальным ценам Y^*. Прибыль и в том и в другом случае одинакова.

Тесная связь между двумя двойственными задачами проявляется не только в равенстве оптимальных значений их целевых функций. Если каждую из двойственных задач решать симплекс-методом, то необходимо привести их к каноническому виду. Для этого в задаче I вводятся m неотрицательных переменных х_n+i, где i=1,2,…m, а во II задаче n неотрицательных переменных y_m+j, где j=1,2,…n. Системы ограничений принимают вид:

Таблица 5

Переменные исходной задачи
Первоначальные переменные				Дополнительные переменные
x1	x2	…	xn	xn+1	xn+2	…	xn+m
ym+1	ym+2	…	ym+n	y1	y2	…	ym
Дополнительные переменные				Первоначальные переменные
Переменные двойственной задачи

Теорема: положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых i выполнено: если х^*_j0, то y^*_m+i=0 и если х^*_j=0, то y^*_m+i0 и аналогично для любых j выполнено: если y^*_j0, то x^*_n+j=0 и если y^*_j=0, то x^*_n+j0.

Вторая теорема двойственности: компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции, выраженной через не основные переменные, ее оптимального решения.

Пример 9:

Если в исходной задаче на последнем шаге выполнения симплекс-метода получили: F=24-4/5x₃-3/5x₄ и F(x^*)=24 - максимум функции, оптимальное решение X^*=(6;4;0;0;1;3), то в двойственной задаче будем иметь: z=24+y₃+3y₄+6y₅+4y₄ z(x^*)=24 - минимум функции, а оптимальным решением будет: Y^*=(4/5;3/5;0;0;0;0).

Соответствие между переменными:

Таблица 6

Переменные исходной задачи
Первоначальные переменные		Дополнительные переменные
x1	x2	x3	x4	х5	x6
y5	y6	y1	y2	y3	y4
Дополнительные переменные		Первоначальные переменные
Переменные двойственной задачи

Замечание: Если в одной из двойственных задач нарушается единственность оптимального решения, то оптимальное решение двойственной задачи вырожденно.

Метод, при котором сначала симплекс-методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находится с помощью теорем двойственности, называется двойственным симплекс-методом. Он применяется в случаях, когда первое базисное решение недопустимо или m>n.