Основы симплекс - метода линейного программирования

Симплекс - метод представляет собой итеративную процедуру решения задач ЛП, в каноническом виде (любую задачу ЛП можно привести к каноническому виду:

(1)

Переменные, входящие с единичными коэффициентами только в одно уравнение системы и с нулевыми - в остальные, называются базисными. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Остальные n-m переменных называются небазисными переменными.

Будем считать, что решается задача на максимум (задачу на минимум можно свести к задаче на максимум, умножив целевую функцию на (-1))

Алгоритм симплекс - метода:

1. После введения добавочных переменных, система уравнений записывается в виде, который называется расширенной системой (1). Предполагается, что все добавочные переменные имеют тот же знак, что и свободные члены.

2. Исходную расширенную систему заносим в первую симплекс таблицу. Последняя строка в которой приведено уравнение для линейной функции цели, называется оценочной. В ней указываются коэффициенты функции цели с противоположным знаком. В левом столбце таблицы записываем базисные переменные (на первом шаге за базисные переменные берутся дополнительные переменные), в первой строке – все переменные, во втором столбце – свободные члены расширенной системы b₁,…,b_m. Последний столбец подготовлен для оценочных отношений, необходимый при расчете. В рабочую часть таблицы, начиная с третьего столбца и второй строки, занесены коэффициенты при переменных a_ij расширенной системы. Далее таблица преобразуется по определенным правилам.

3. Проверяем выполнение критерия оптимальности (при решении задачи на максимум критерий оптимальности состоит в отсутствии отрицательных коэффициентов в оценочной строке). Если критерий оптимальности выполнен, то следовательно, максимум достигнут и оптимальное значение z равно с₀ (в левом нижнем углу таблицы). Базисные переменные принимают значения b_i, остальные переменные равны 0. Если критерий оптимальности не выполнен, переходим к следующему шагу.

4. По оценочной строке выбираем переменную вводимую в базис. Находим наибольший по модулю отрицательный коэффициент в оценочной строке. Соответствующая этому столбцу переменная х_s будет вводимой в базис, а сам столбец называется разрешающим.

5. Находим переменную, выводимую из базиса. Для этого составляем оценочные отношения (они заносятся в столбец для оценочных отношений) по следующим правилам:

   1. , если b_i и a_is имеют разные знаки;

   2. , если b_i=0 и a_is<0;

   3. , если a_is=0;

   4. 0, если b_i=0 и a_is>0;

   5. , если b_i и a_is имеют одинаковые знаки.

Определяем 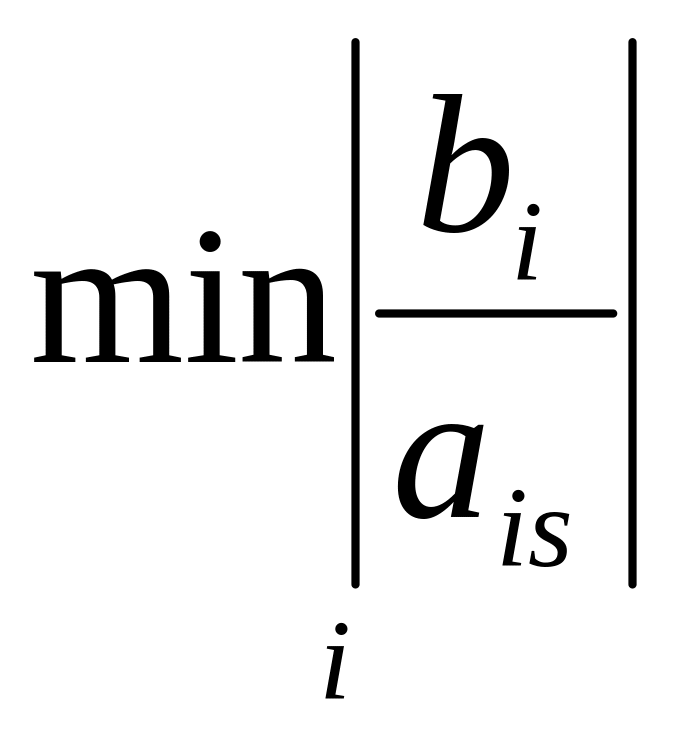. Если конечного минимума нет, то задача не имеет конечного оптимума (z_max=). Если минимум конечен, то выбираем строку q, на которой он достигается (если их несколько, то любую), и называем ее разрешающей строкой. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент a_qs.

6. Переходим к следующей таблице по правилам (преобразования Гаусса-Жордана):

   1. в левом столбце записываем новый базис: вместо основной переменной x_q – переменную x_s;

   2. в столбцах, соответствующих базисным переменным, проставляем нули и единицы: 1- на пересечении строки и столбца, соответствующих одной и той же базисной переменной; 0 – во всех других позициях столбцов базисных переменных;

   3. Новую строку q получаем из старой делением на разрешающий элемент a_qs;

   4. все остальные элементы а_ij^' вычисляем по правилу:

(2)

Далее переходим к шагу III.

Пример 6.

Решим задачу:

Приведем систему ограничений к каноническому виду. Получим расширенную систему:

Целевую функцию представим в виде z-2x₁-3x₂=0.

Базисными переменными будут являться дополнительные переменные x₃, x₄, x₅, x₆.

Заполним первую симплекс-таблицу:

Базис	Свобод-ный член	Переменные						Оценоч-ные отношения
		x1	x2	x3	x4	x5	x6
x3	18	1	3	1	0	0	0	18/3
x4	16	2	1	0	1	0	0	16
x5	5	0	1	0	0	1	0	5
x6	21	3	0	0	0	0	1	
z	0	-2	-3	0	0	0	0

Проверяем критерий оптимальности задачи. В последней оценочной строке имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю – (-3). Следовательно s=2, переменная х₂ является выводимой из базиса, а соответствующий ей столбец – разрешающим.

Находим оценочные отношения и выбираем из них минимальное (=5). Следовательно, q=3, переменная х₅ является вводимой в базис, а соответствующая ей строка – разрешающей.

Переходим к новой симплекс-таблице:

1. в новом базисе основные переменные x₃, x₄, x₂, x₆;

2. расставляем 0 и1; например, на пересечении столбца и строки, соответсвущих переменной х₃ ставим 1, а остальные элементы столбца х₃ равны 0 и т.д. Третья строка получается делением на разрешающий элемент а₃₃=1. Остальные клетки таблицы заполняем по формулам (2). Например:

Получаем вторую симплекс таблицу:

Базис	Свобод-ный член	Переменные						Оценоч-ные отношения
		x1	x2	x3	x4	x5	x6
x3	3	1	0	1	0	-3	0	3
x4	11	2	0	0	1	-1	0	11/2
x2	5	0	1	0	0	1	0	
x6	21	3	0	0	0	0	1	7
z	15	-2	0	0	0	3	0

Критерий оптимальности вновь не выполнен. Теперь разрешающий первый столбец и х₁ – вводимая переменная. Считаем оценочные отношения и находим разрешающую строку – первая и выводимую из базиса переменную – х₃. Разрешающий элемент а₁₁.

Переходим к новой симплекс-таблице:

Базис	Свобод-ный член	Переменные						Оценоч-ные отношения
		x1	x2	x3	x4	x5	x6
x1	3	1	0	1	0	-3	0	
x4	5	0	0	-2	1	5	0	5/5
x2	5	0	1	0	0	1	0	5/1
x6	12	0	0	-3	0	9	1	12/9
z	21	0	0	2	0	-3	0

И на этот раз критерий оптимальности не выполнен.

Выводимая переменная х₄; вводимая х₅. Переходим к новой таблице.

Базис	Свобод-ный член	Переменные						Оценоч-ные отношения
		x1	x2	x3	x4	x5	x6
x3	6	1	0	-1/5	3/5		0
x5	1	0	0	-2/5	1/5	1	0
x2	4	0	1	2/5	-1/5	0	0
x6	3	0	0	3/5	-9/5	0	1
z	24	0	0	4/5	3/5	0	0

Критерий оптимальности выполнен, значит z_max=24. Оптимальное решение (6; 4; 0; 0; 1; 3).