Алгоритм решения злп графическим методом.

(число переменных n=2)

1. Строится многоугольная область допустимых решений на плоскости х₁Ох₂, соответствующая ограничениям. Затем строится вектор-градиент целевой функции z в любой точке х₀, принадлежащей области допустимых решений.

2. Прямая (линии уровня функции z), перпендикулярная вектору-градиенту, передвигается параллельно самой себе в направлении вектора-градиента в случае задачи на максимум (в противоположном направлении – в случае задачи на минимум) до тех пор, пока она не покинет область допустимых решений. Предельная точка (или точки) области являются оптимальными точками.

3. Чтобы найти координаты оптимальной точки, надо решить систему уравнений, которая соответствует прямым, пересечение которых образует эту точку. Значение целевой функции в этой точке будет оптимальным, а сами координаты точки будут являться решением задачи ЛП.

Пример 5.

Решить геометрически задачу:

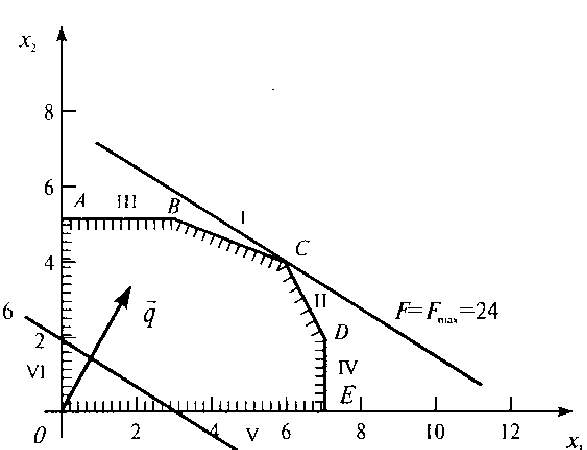
Построим многоугольник всех допустимых решений OABCD и направляющий вектор целевой функции _z (см. рис.1). Направление вектора-градиента указывает направление возрастания целевой функции. Так как рассматриваемая задача на отыскание максимума, то прямую, перпендикулярную вектору _z перемещаем в направлении этого вектора параллельно самой себе до тех пор, пока эта прямая не покинет область допустимых решений. На границе области, в нашем случае в точке С, и будет решение задачи. Точка С находится на пересечении (1) и (2) прямых и, следовательно, ее координаты определяются решением системы уравнений: , откуда х₁=6, х₂=4, т.е. точка С имеет координаты (6,4).

М

Рисунок 1

аксимум (максимальное значение целевой функции) равен:

z=26+34=24

Итак, ответ: z=24 при оптимальном решении х₁=6, х₂=4, т.е. максимальна прибыль может быть достигнута при производстве 6 единиц первой и 4 единиц второй продукции.

Задания:

Решить задачи графическим методом:

Задача № 1

Задача № 2

Задача № 3

Задача № 4

Задача № 5

Задача № 6

Особые случаи задач линейного программирования.

(графический метод)

Неограниченность области допустимых решений.

Решим геометрически следующую задачу:

Из рисунка 2 видно, что область допустимых значений неограниченна. Перемещая линию уровня функции z в направлении убывания целевой функции (т.е. в направлении, противоположном вектору_z), убедимся, что она всегда будет пересекать область допустимых значений, следовательно целевая функция неограниченно убывает.

Ответ будет звучать следующим образом: конечного оптимума целевая функция не имеет, z=-.

Внимание! В некоторых случаях неограниченности области допустимых решений целевая функция может достигать своего оптимума.

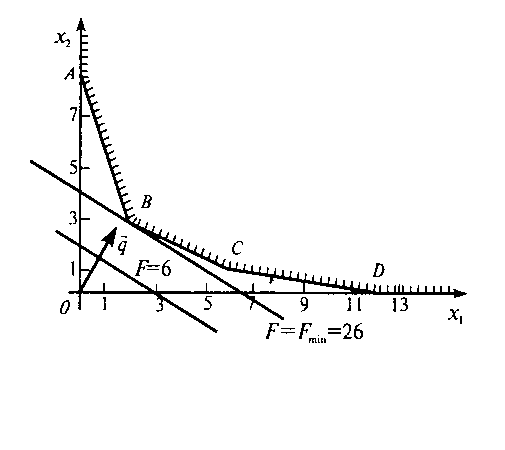
Рисунок 2

Не единственность оптимального решения.

Рассмотрим задачу:

Геометрическое решение задачи показано на рисунке 3. Из него следует, что линия уровня с максимальным уровнем совпадает с граничной линией АВ области допустимых решений ABCD, т.е. с линией х₁+х₂=8 (Внимание! Данная ситуация возможна только в том случае, если коэффициенты целевой функции пропорциональны коэффициентам какой-либо прямой ограничений. Это условие необходимое, но не достаточное.). Следовательно на всем отрезке АВ целевая функция z принимает одно и то же оптимальное значение. Это означает, что задача имеет бесконечное множество оптимальных решений (их задают координаты отрезка АВ), среди которых базисных оптимальных решений два -–соответственно в угловых точках А(3,5) и В(6,2) (точки находим решая соответствующие уравнения). Точки отрезка АВ задаются как линейная комбинация точек А и В:

Максимальное значение целевой функции можно найти подставив координаты любой точки отрезка АВ в уравнение целевой функции.

В нашем случае z=24.

Рисунок 3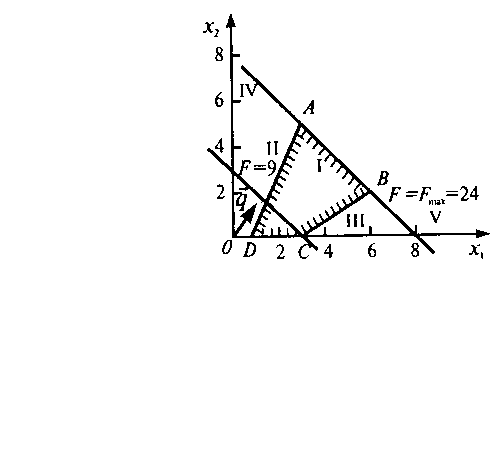

Задания:

Решить задачи геометрически:

1.

2.

3.

4.

5.

6.

7.