Лабораторная работа №1 Исследование характеристик дифференцирующей цепи

1. Цель работы: овладение методами измерения основных характеристик линейной цепи (звена).

2. Теоретические основы

Дифференцирующей называется электрическая цепь, в которой выходная величина пропорциональна производной от входной величины. Простейшими дифференцирующими цепями могут служить цепи с емкостью или индуктивностью (рис.2.1).

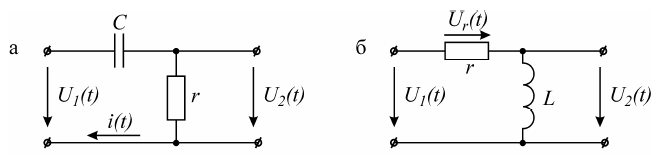
Рис.2.1 Простейшие дифференцирующие цепи

В цепи с емкостью

Принимая u_c (t) за входную величину, а ток i_c (t) – за выходную, получим дифференцирующую цепь.

В цепи с индуктивностью

Принимая i_L(t) за входную величину, а u_L(t) – за выходную, получим дифференцирующую цепь.

Использовать ток как входную или выходную величину практически затруднительно, так как в первом случае необходимо иметь стабильный источник тока, а во втором для его измерения необходимо включить последовательно дополнительное сопротивление, которое оказывает влияние на процесс. Следовательно, входной и выходной величинами целесообразно выбирать напряжения, при этом используются rC - и rL – цепи. На практике широкое распространение получила rC - цепь.

Условие, при котором rC-цепь выполняет операцию дифференцирования, вытекает из уравнения

Если принять

то

При синусоидальном входном напряжении уравнение цепи в комплексной форме

По условию дифференцирования

тогда

или

При несинусоидальной форме напряжения U₁(t) условие дифференцирования должно быть выполнено для всех гармонических составляющих входного сигнала. При этом условием дифференцирования является

где ω_В – частота наивысшей гармоники, которой нельзя пренебречь.

Идеальное дифференцирование прямоугольного импульса показано на рис. 2.2,а. Амплитуда выходного сигнала u₂(t) бесконечно велика.

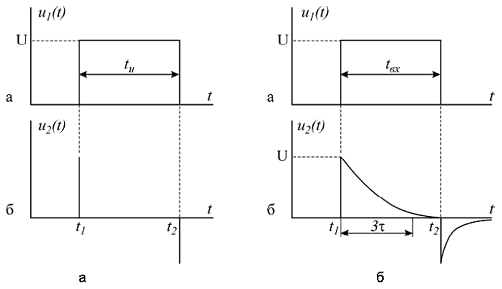
Рис.2.2 Идеальное (а) и реальное (б) дифференцирование прямоугольного импульса

График напряжения u₂(t) на выходе реальной дифференцирующей цепи показан на рис.2.2,б. Напряжение u₂(t) представляет собой импульсы экспоненциальной формы с чередующейся полярностью.

За длительность выходного импульса принимают время, равное утроенному значению постоянной времени цепи . Амплитуда импульсов равна величине входного напряжения. Сравнение временных диаграмм реальной и идеальной дифференцирующей цепи (рис.1,а и 1,б) показывает, что при уменьшении τ длительность импульсов u₂(t) сокращается и кривая u₂(t) стремится по форме к производной входного напряжения. Величина τ называется постоянной времени цепи и соответствует изменению выходного напряжения на 63% от исходного (e^-1 = 0.37). Очевидно, что время изменения выходного напряжения зависит от сопротивления резистора и емкости конденсатора и, соответственно, постоянная времени цепи пропорциональна этим значениям, т. е. τ = RC (в секундах).

Дифференцирующая цепь называется еще укорачивающей, так как длительность выходных импульсов значительно меньше, чем входных.

Допустим, конденсатор разряжен. При подаче на вход RC-цепи импульса напряжения конденсатор сразу же начнет заряжаться током, проходящим через него самого и резистор. Сначала ток будет максимальным, затем по мере увеличения заряда конденсатора постепенно уменьшится до нуля по экспоненте. Когда через резистор проходит ток, на нем образуется падение напряжения, которое определяется, как U=i R, где i-ток заряда конденсатора. Поскольку ток изменяется экспоненциально, то и напряжение будет изменяться также - экспоненциально от максимума до нуля. Падение напряжения на резисторе как раз и является выходным, величину которого можно определить по формуле U_вых = U₀e^-t/τ.

Передаточная функция цепи (коэффициент передачи) - равна отношению комплексной амплитуды сигнала на выходе к комплексной амплитуде сигнала на входе:

, где - фазово-частотная характеристика, - амплитудно-частотная характеристика цепи.

Импульсная характеристика g(t) - реакция цепи на действие сигнала в виде δ-функций, т. е. это сигнал на выходе, если сигнал на входе есть d-функция.  при . При этом g(t) = 0 при t < 0 – выходной сигнал не может возникнуть ранее момента появления входного сигнала.

Импульсная характеристика цепи и передаточная функция связаны преобразованием Фурье:

Переходная характеристика цепи h(t) - является откликом на сигнал, называемый единичным скачком: h(t) = 1 при t >0, h(t) = 0 при t < 0, при этом

Для дифференцирующей цепи:

Комплексный коэффициент передачи: ,