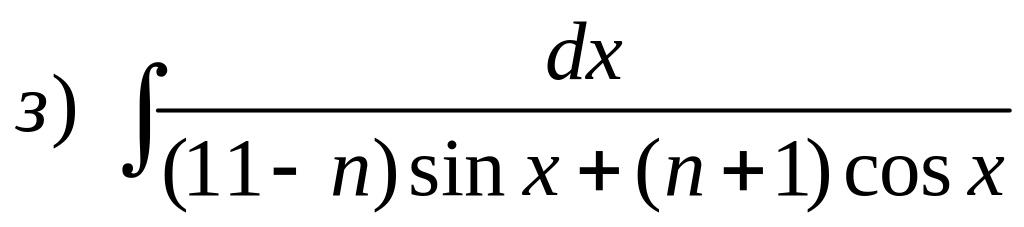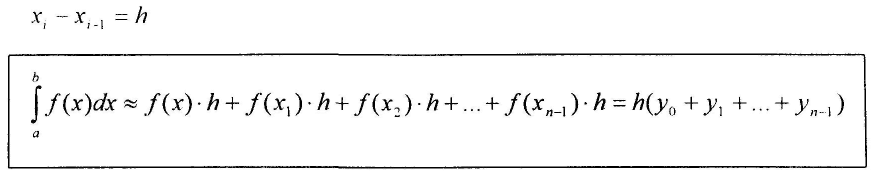- •Аннотация.
- •Содержание.
- •3. Заключение………………………………………………………………………
- •Введение.
- •Основная часть.
- •1.1.Список практических работ.
- •1.2. Ход выполнения практической работы
- •1.3 Критерии оценивания практических работ
- •1.4 Практические работы 1-15. Практическая работа №1
- •Ход работы.
- •Практическая работа №2
- •Ход работы.
- •Решение.
- •Практическая работа №3
- •Ход работы.
- •Контрольные вопросы:
- •Практическая работа №4
- •Ход работы.
- •Практическая работа №5
- •Ход работы.
- •Практическая работа №6
- •Ход работы.
- •Контрольные вопросы:
- •2) Для закрепления теоретического материала и получения прочных знаний решить примеры:
- •Формула Симпсона.
- •2).Контрольные вопросы:
- •Практическая работа №11
- •Ход работы.
- •Практическая работа 12
- •Ход работы.
- •1). Повторение теоретического материала и образцы решения задач:
- •2) Для закрепления теоретического материала и получения прочных знаний
- •Практическая работа 13
- •Дифференциальные уравнения первого порядка.
- •2. Методы решения основных типов дифференциальных уравнений
- •3.Решение задачи Коши для дифференциальных уравнений 1-ого порядка методом Эйлера.
- •Практическая работа 14
- •Методы решения дифференциальных уравнений 2-го порядка, допускающих понижение порядка
- •Практическая работа 15
Контрольные вопросы:
1.Что называется производной функции в данной точке?
2.Чему равен угловой коэффициент касательной к функции в данной точке?
3.Каков физический смысл производной?
4.Сформулировать правила дифференцирования.
5.Основные табличные производные.
6.Условия монотонности, выпуклости функции на заданном промежутке.
7.Уравнение касательной и нормали к графику функции.
8. Физический смысл первой и второй производных.
2) Для закрепления теоретического материала и получения прочных знаний решить примеры:
1.Найти производные функций в данных точках( n- номер варианта):
1.1.![]() в точке
в точке
![]() .
.
1.2.
![]() в точке
в точке
![]() .
.
1.3.
![]() в
точке
в
точке
![]() .
.
1.4.
![]() в точке
в точке
![]() .
.
1.5.
![]() в точке
.
в точке
.
1.6.
![]() в точке
в точке
1.7.
![]() в
точке
в
точке
![]() .
.
1.8.
![]() в
точке
в
точке
![]() .
.
1.9.
![]() в точке
.
в точке
.
1.10.
![]() в точке
в точке
![]() .
.
1.11.![]() в точке
в точке
![]() .
.
1.12.
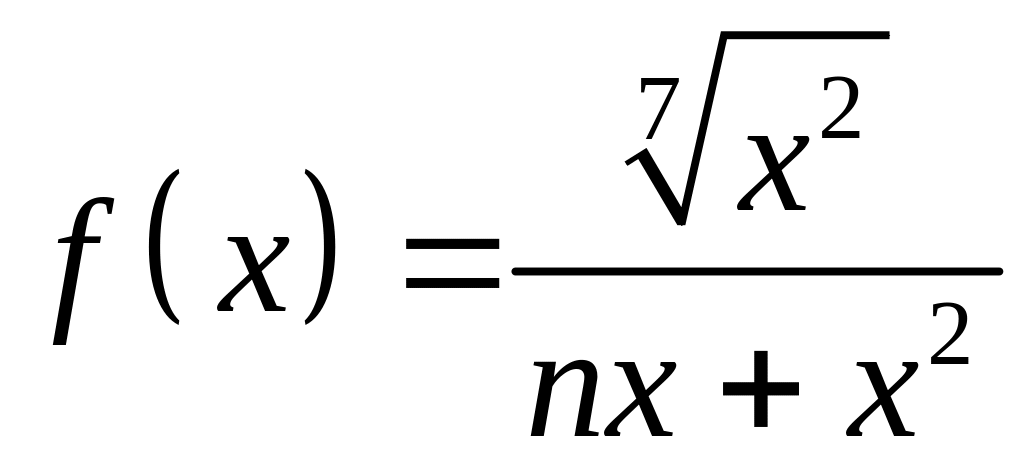 в точке
.
в точке
.
2. Написать уравнение касательной к графику функции в данных точках ( n- номер варианта):
1.13.
![]() в точке
.
в точке
.
2.1.
![]() в точке
.
в точке
.
2.2.
![]() в точке
в точке
![]() .
.
3. Найти уравнение
касательной к графику функции а)![]() в точке
.
в)
в точке
.
Сделать чертежи. ( n- номер
варианта)
в точке
.
в)
в точке
.
Сделать чертежи. ( n- номер
варианта)
4.
Точка движется прямолинейно по
закону
![]() (
(![]() -в
метрах,
-в
метрах,
![]() -в
секундах). Найти скорость движения через
2 секунды после начала движения. ( n-
номер варианта)
-в
секундах). Найти скорость движения через
2 секунды после начала движения. ( n-
номер варианта)
в1. Провести исследование функций и построить графики:
в2. Провести
исследование функций и построить
графики:
в3. Провести исследование функций и построить графики:
в4. Провести исследование функций и построить графики.
в5. Провести исследование функций и построить графики:
в6. Провести исследование функций и построить графики:
в7. Провести исследование функций и построить графики:
В8. Провести исследование функций и построить графики:
В9. Провести исследование функций и построить графики:
В10. Провести исследование функций и построить графики:
В11. Провести исследование функций и построить графики:
В12. Провести исследование функций и построить графики:
В13. Провести исследование функций и построить графики:
В14. Провести исследование функций и построить графики:
В15. Провести исследование функций и построить графики:
Практическая работа №7
Тема: Приближенное решение алгебраических и трансцендентных уравнений. Цель работы: уметь отделять корни уравнения графически и аналитически; уметь уточнять корни уравнения методом половинного деления, методом хорд, методом касательных ( Ньютона) и методом итераций.
Ход работы.
1). Повторить краткие теоретические сведения и разобрать задачи с решениями: Графический способ отделения корней уравнения
Записываем уравнение в виде:
.
Пример: Отделить все
действительные корни для уравнения
:
Решение.
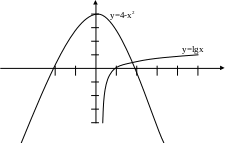
Запишем уравнение в виде:
Строим графики левой и правой частей уравнения на одном чертеже. y = lgx
y = 4-x2
Количество перемен знака равно количеству корней.
Примеры:
Решение.
Пусть
7x6-18x5=0 x5(7x-18) =0
x5=0 7x-18=0
x=0 и x=
2.. Отделить все действительные корни для уравнения :
Решение. Отделим корни расчетным путем. Для этого:
Найдем производную функции
Приравниваем производную 0:
Решаем квадратное уравнение.
Следовательно, уравнение имеет
единственный корень. Найдем знак
функции
в точке
Следовательно, корень уравнения
находится на промежутке
Метод половинного деления для решения уравнений
Дана функция f(x)=0,
корень отделён на промежутке
Требуется отделить корень с точностью
Определяем знак
Выбираем тот конец, на котором значение функции имеет противоположный знак.
Определяем знак f(x1)
и т.д. Процесс заканчиваем, когда
Пример:
-
+
a
b
-2
-1
-1,5
-1
-1,25
-1
-1,13
-1
-1,13
-1,07
Ответ: -1;1
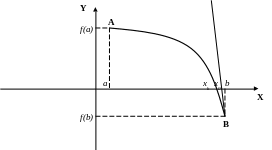
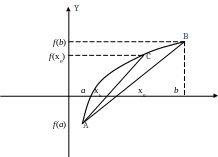
Метод касательных (Ньютона) для решения уравнений.
Дана функция f(x)=0, корень отделён на промежутке . На этом промежутке первая и вторая производные имеют постоянный знак.
Y
f’’(x)<0
A
f(b) f’(x)>0; f’’(x)>0
f(a)
Случай 3: f’(x)<0; f ’’(x)<0
Формула такая же как во втором случае
f’(x)<0; f ’’(x)<0
Формула такая же как в случае 1
Мнемоническое правило. В методе касательных за неподвижный конец принимаем тот, в котором знак функции совпадает со знаком второй производной.
Пример:
Критических точек нет.
a = -1 – подвижный конец
Ответ:
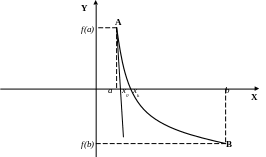
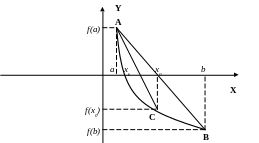
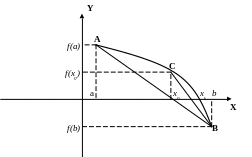
Метод хорд для решения уравнений
Дана функция f(x)=0, корень отделён на промежутке . На этом промежутке первая и вторая производные (f'(x) и f''(x)) имеют постоянный знак.
I. Случай (Знаки производных различны).
f(a)<0, f(b)>0
X
Формулы те же самые.
Y
xk –корень уравнения
Формула такая же как в случае, когда f'(x)>0, f''(x)>0
Мнемоническое правило. В метоле хорд за неподвижный конец принимаем тот, в котором знак второй производной f''(x) совпадает со знаком функции.
Пример: Отделить корни и
уточнить их методом хорд
f’>0
b=2 – неподвижный конец
Метод итераций для решения систем уравнений
Дана функция f(x)=0, корень отделён на промежутке . Из данного уравнения выразим x. Это всегда возможно, например:
или
Запишем уравнение в виде
Строим график левой и правой части
За нулевое приближение выбираем любое
число из промежутка
Находим
Находим погрешность:
Если погрешность больше требуемой,
то продолжаем процесс итерации:
Находим погрешность:
Если погрешность больше требуемой,
то продолжаем процесс итерации:
Пока не получим , где - требуемая погрешность.
метод касательных:
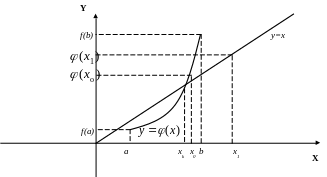
Ответ: -1;4 Условия сходимости итерационного процесса Теорема «О сходимости итерационного процесса»
Итерационный процесс сходится независимо от выбора начального приближения x0, если:
1)
2)
3) Существует такое число q<1,
что
Пусть
Итерационный процесс сходится, если
функцию представить в виде
Пример:
Ответ: 3,51
2). Контрольные вопросы: 1) Способы отделения корней уравнения. 2) Способы уточнения корней уравнения.
3). Выполнить задания. n – номер варианта Задание 1. Отделить корни уравнения графически:
Задание 2. Отделить корни уравнения аналитически:
11
Задание 3.
Приближенно найти все корни уравнения
с точностью
, используя а) метод половинного деления. б) метод касательных. в) метод хорд. г) метод итераций.
Практическая работа №8
Тема: Методы вычисления неопределенного интеграла.
Цель работы: уметь вычислять неопределенные интегралы различными методами. Непосредственное интегрирование, замена переменных, внесение под знак дифференциала. Интегрирование по частям. Интегрирование функций, содержащих квадратный трехчлен. Интегрирование рациональных дробей. Интегрирование тригонометрических функций.
Ход работы.
1). Повторить краткие теоретические сведения и разобрать задачи с решениями.
Функция F(x) называется первообразной для функции f(x) на интервале (a, b), если для всех x из этого интервала выполняется равенство
Неопределенным
интегралом
от функции f(x)
называется множество всех первообразных
этой функции, то есть неопределенный
интеграл – это выражение вида
Процедуру нахождения неопределенного интеграла называют интегрированием. Таблица интегралов
2. Свойства неопределенного интеграла. Интегрирование методом подведения под знак дифференциала части подинтегральной функции При интегрировании функций наиболее часто используются следующие его свойства:
1)
2)
3)
Пример 1.
Найти
Решение. Воспользуемся свойствами 1-3, а также таблицей интегралов:
Ответ: . Иногда при интегрировании удобно использовать свойство дифференциала:
Пример 2.
Найти
Решение. Согласно формуле (2) можно записать:
Теперь воспользуемся свойством 2, а также таблицей интегралов:
Инвариантность формул интегрирования позволяет применять при интегрировании подведение под знак дифференциала части подинтегральной функции, основанное на следующей формуле:
Пример 3.
Найти
Решение. Воспользуемся методом подведения под знак дифференциала, а также таблицей интегралов:
=
Ответ:
3. Интегрирование по частям Формулой интегрирования по частям называют следующую формулу:
Обычно за
Можно выделить два основных класса интегралов, берущихся по частям:
1)
– здесь за u
принимают
многочлен
2)
– здесь за u
принимают обратную функцию, например,
arcsinbx,
за
– оставшееся
выражение, то
есть
4. Интегрирование рациональных дробей
Рациональной
дробью
где k,
r
– целые положительные числа, а трехчлен
5. Интегрирование некоторых тригонометрических функций
Для нахождения
интегралов видов
Для нахождения
интегралов вида
6. Вычисление определенного интеграла по формуле Ньютона–Лейбница Формула Ньютона–Лейбница для вычисления определенного интеграла имеет вид:
если
и
Пример 4.
Вычислить определенный интеграл Решение. Это определенный интеграл, берущийся по частям, поэтому, применяя формулу (4), а затем формулу Ньютона–Лейбница, получаем:
= Ответ:
Примеры: Задача 1. Найти неопределенные интегралы:
В примерах
Задача 2. Вычислить несобственные интегралы или доказать их расходимость:
а) Задача 3.
а)
Вычислить
с помощью определенного интеграла
площадь фигуры, ограниченной в ДСК
линиями l1:
б)
Вычислить
с помощью определенного интеграла
площадь фигуры, ограниченной в ПСК
линией l:
Задача 4. Вычислить с помощью определенного интеграла объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями
l1:
Задача 5.
Вычислить
с помощью определенного интеграла
длину дуги кривой, заданной в ДСК
уравнением
Решение задачи 1.
а)
Так как
Проверим результат дифференцированием:
следовательно, выполнено условие (1).
Ответ:
б)
Интеграл
Проверим результат дифференцированием:
Ответ:
в) Подинтегральная функция является правильной рациональной дробью, поэтому ее можно представить в виде суммы простейших дробей:
Неопределенные коэффициенты А, В, С найдем, приравнивая коэффициенты при одинаковых степенях х в левой и правой частях тождества:
Коэффициенты А, В, С можно найти другим способом – подставляя в тождество «удобные» значения х (метод отдельных значений):
Из первого
уравнения получим:
Таким образом,
Переходим к интегрированию:
Здесь использовано:
Проверим результат
дифференцированием:
Ответ:
г) Применим универсальную тригонометрическую подстановку:
Возвращаясь к переменной х, получаем:
Ответ:
2) Ответить на контрольные вопросы:
3) Выполнить задания. Задача 1. Найти неопределенные интегралы (n-номер варианта):
Практическая работа 9 .
Тема: Приложения определенного интеграла.
Цель работы: уметь применять определенные интегралы для вычисления площади плоской фигуры, длины дуги кривой, объема тела вращения.
Ход работы.
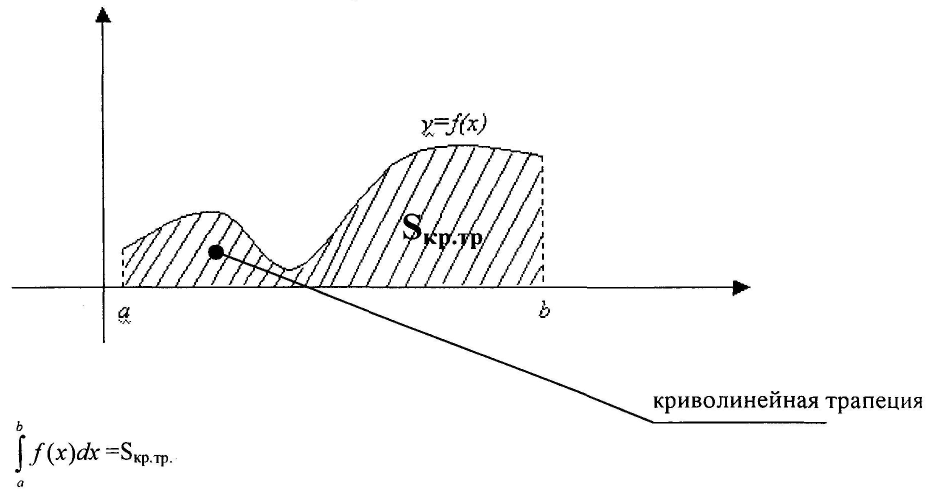
1). По пособию Подольского В.А., Суходского А.М., Мироненко Е.С. «Сборник задач по математике» М.: Высш. шк., 2008 г. повторить теоретические сведения и разобрать задачи с решениями: гл.13§3-7 Контрольные вопросы:
1. Какая фигура называется криволинейной трапецией? 2. Чему равна площадь криволинейной трапеции в прямоугольных координатах? 3. Чему равна площадь криволинейной трапеции в полярных координатахкоординатах? 4. Как найти объем тела вращения?
2). Для закрепления теоретического материала и получения прочных знаний решить примеры по образцу.
1;16в. №№13.67; 13.82; 13.98 2;17в. №№ 13.68; 13.83; 13.99 3;18в. №№13.69; 13.84; 13.100 4;19в. №№13.70; 13.85; 13.101 5;20в. №№13.71; 13.86; 13.102 6;21в. №№13.72; 13.87; 13.103 7;22в. №№13.73; 13.88; 13.104 8;23в. №№13.74; 13.89; 13.105 9;24в. №№13.75; 13.90; 13.106 10;25в. №№13.76; 13.91; 13.107 11;26в. №№13.77; 13.92; 13.110 12-27в. №№13.78; 13.93; 13.111 13-28в. №№13.79; 13.94; 13.112 14;29в. №№13.80; 13.95; 13.113 15;30в. №№13.81; 13.97; 13.114
Практическая работа № 10
Тема: Методы вычисления неопределенного интеграла.
Цель работы: уметь вычислять интегралы по формулам прямоугольников, трапеций и Симпсона и находить погрешность полученных значений интеграла методом двойного пересчета.
Ход работы.
1). Повторить краткие теоретические сведения и разобрать задачи с решениями:
Постановка задачи численного интегрирования. Требуется вычислить интеграл
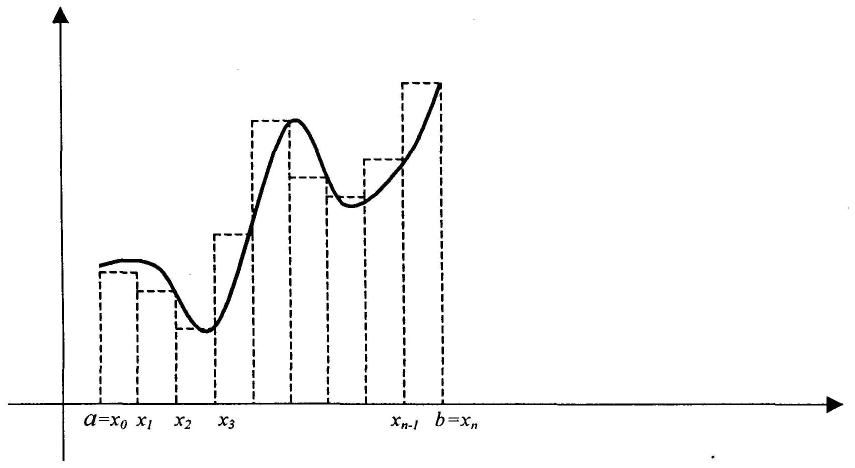
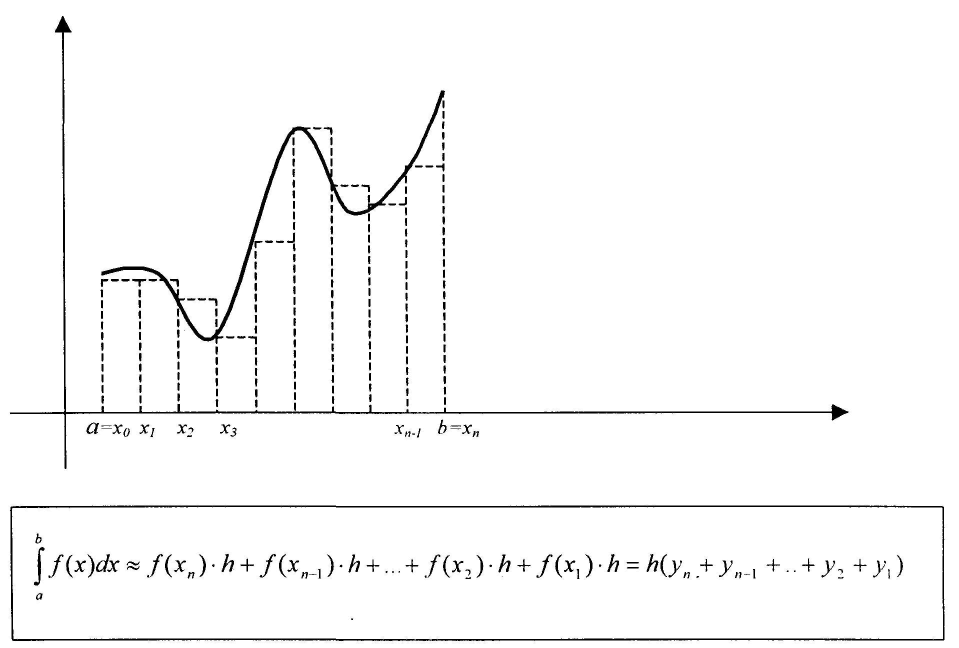
Задача численного интегрирования - заменить криволинейную трапецию простой геометрической фигурой: прямоугольником, трапецией и др. Формула прямоугольников Левосторонняя формула прямоугольников:
Расстояние между соседними значениями х обозначается h и называется шагом интегрирования.
Правосторонняя формула прямоугольников:
Пример:
Вычислить интеграл следующими способами:
|
2)
![]()
+ 0,16807 + 0,32768 + 0,59049) = 0,120834
3)
![]()
+0,59049+1)=0620824
Среднее арифметическое:
= 0,164537*0,16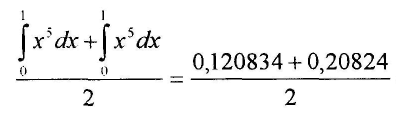
Погрешность формулы прямоугольников (см. Приложение)
Формула трапеций.
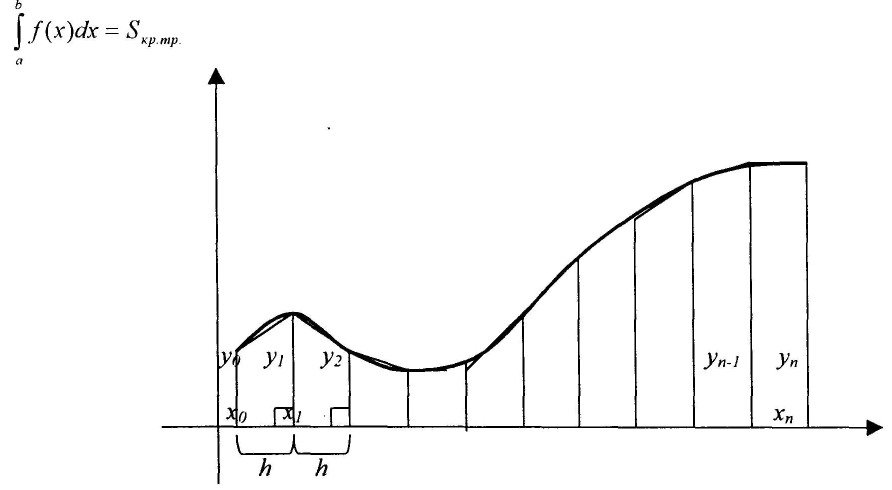
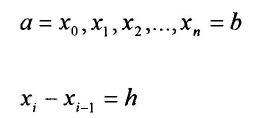
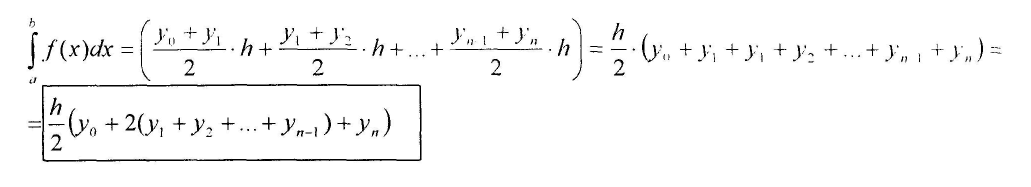
Пример:

= 0,05 • (1 + 2(1,21 +1,44 +1,69 +1,96 + 2,25 + 2,56 + 2,89 +
3,24 + 3,61) + 4) = 2,34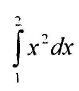
= 2,34-2,33 =0,01![]()

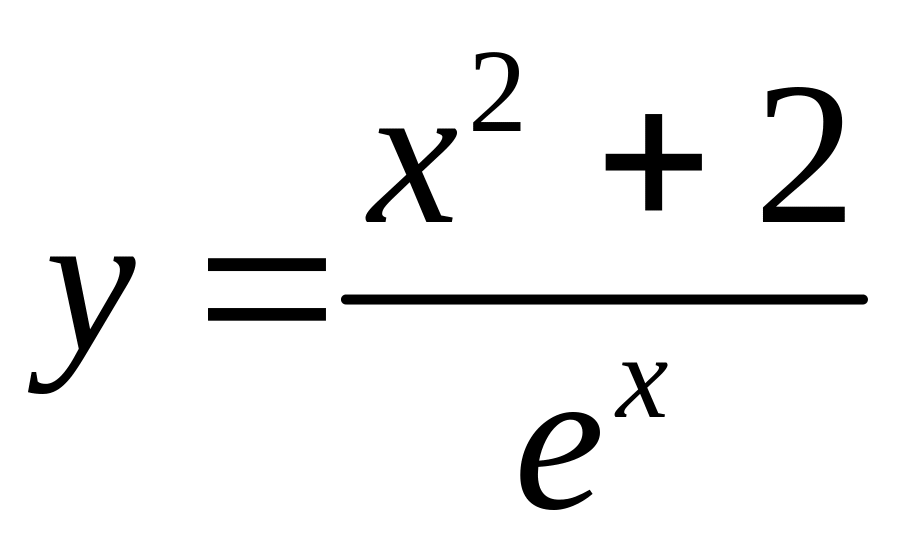
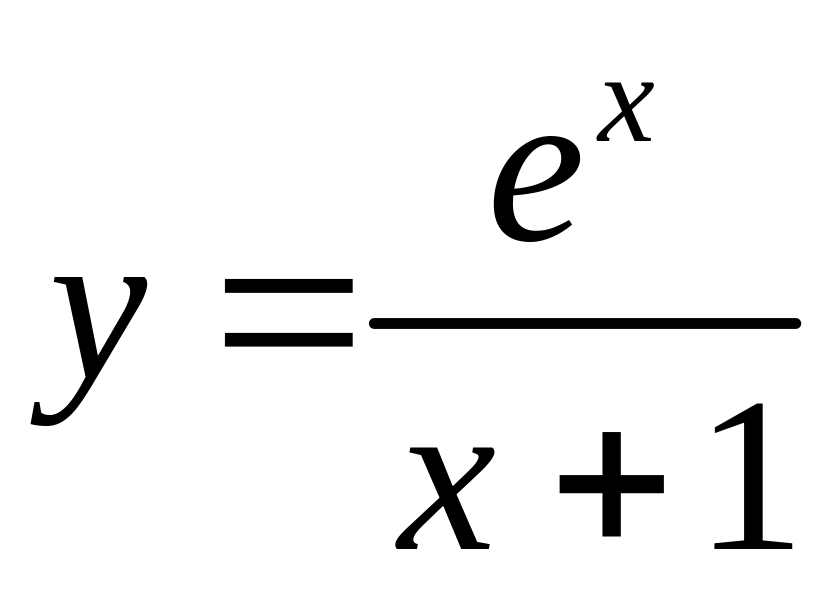


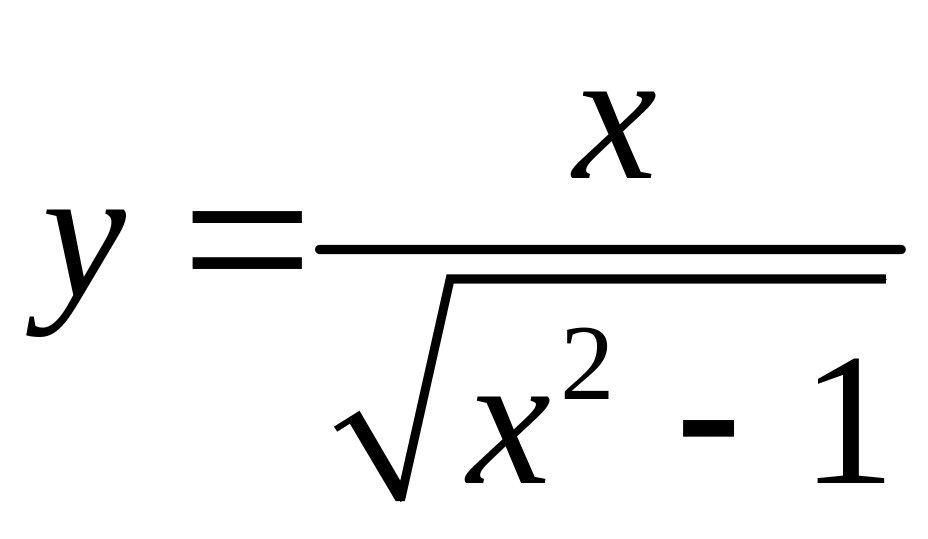
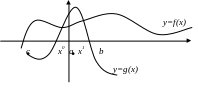



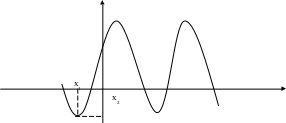 Аналитическое
отделение корней уравнения
Аналитическое
отделение корней уравнения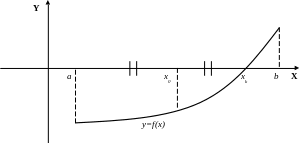

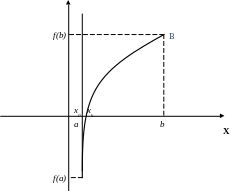 f’(x)>0;
f’(x)>0;



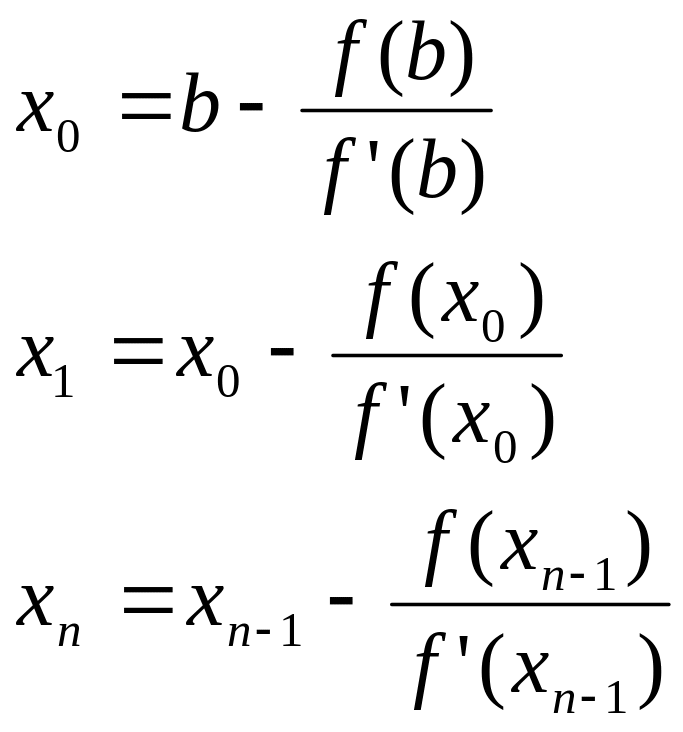
 Случай
4:
Случай
4: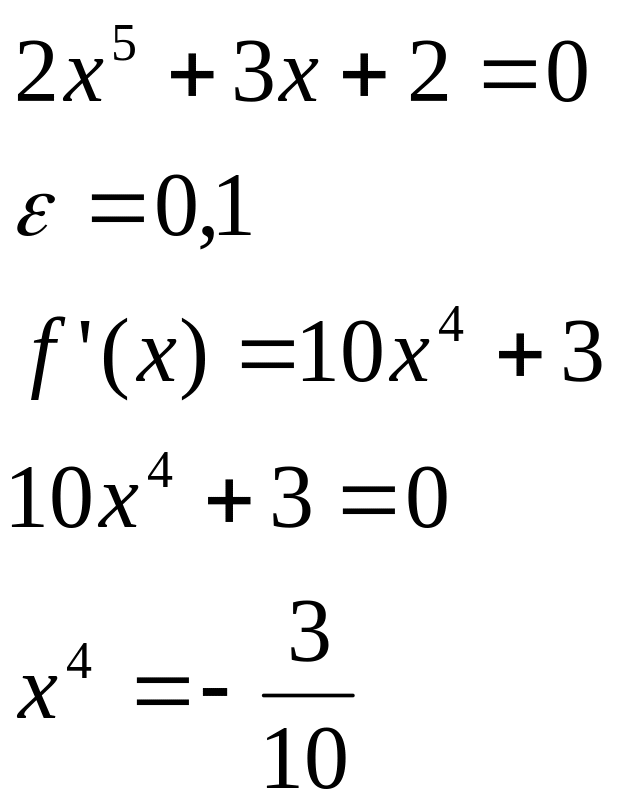
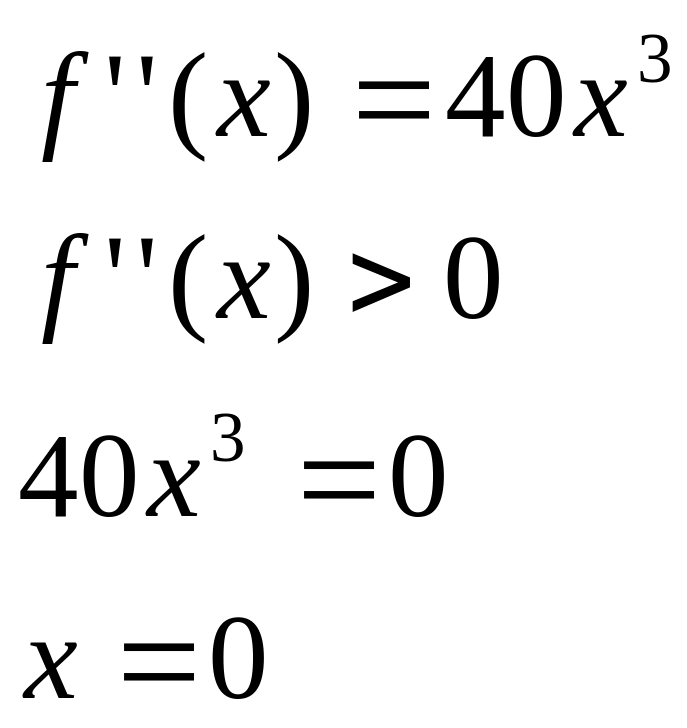

 f'(x)>0,
f''(x)<0
f'(x)>0,
f''(x)<0

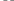 xk
–корень уравнения
xk
–корень уравнения


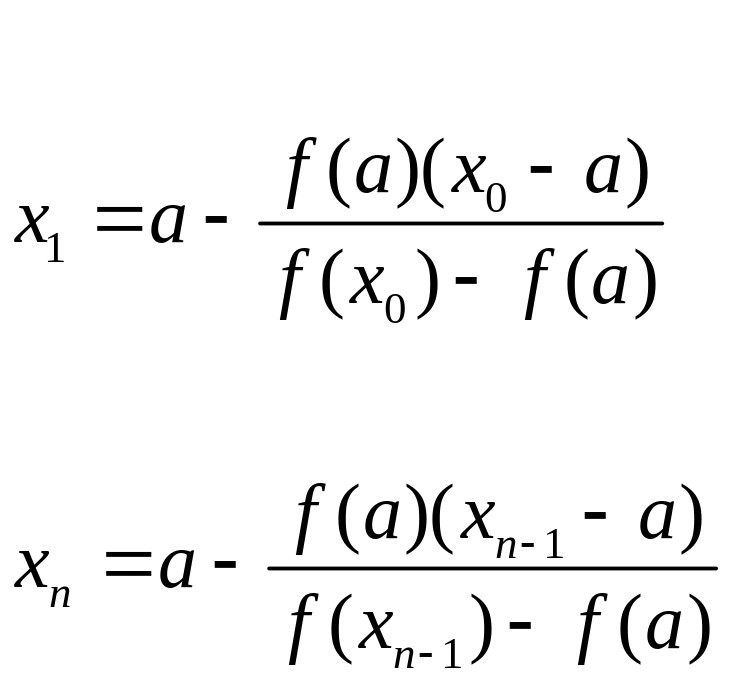
 f'(x)<0,
f''(x)>0
f'(x)<0,
f''(x)>0
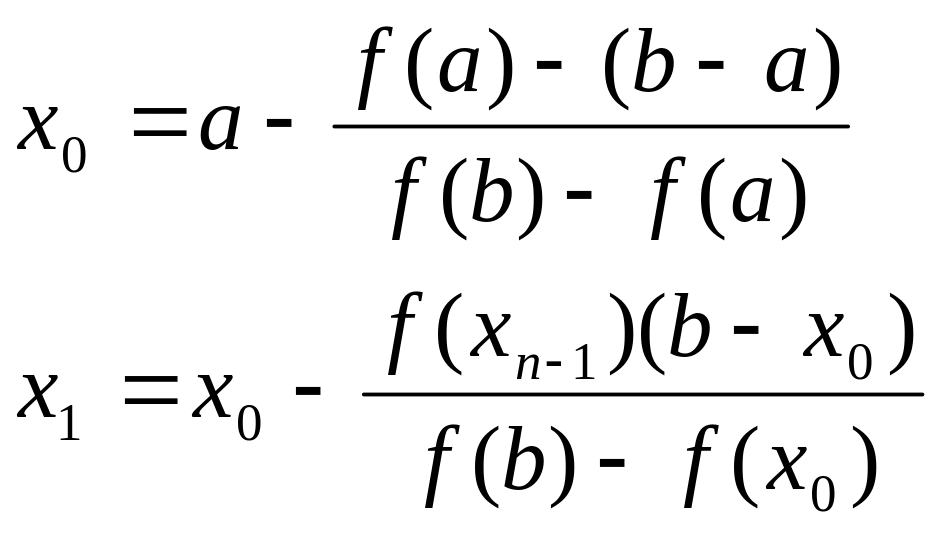

 2)
f'(x)<0,
f''(x)<0
2)
f'(x)<0,
f''(x)<0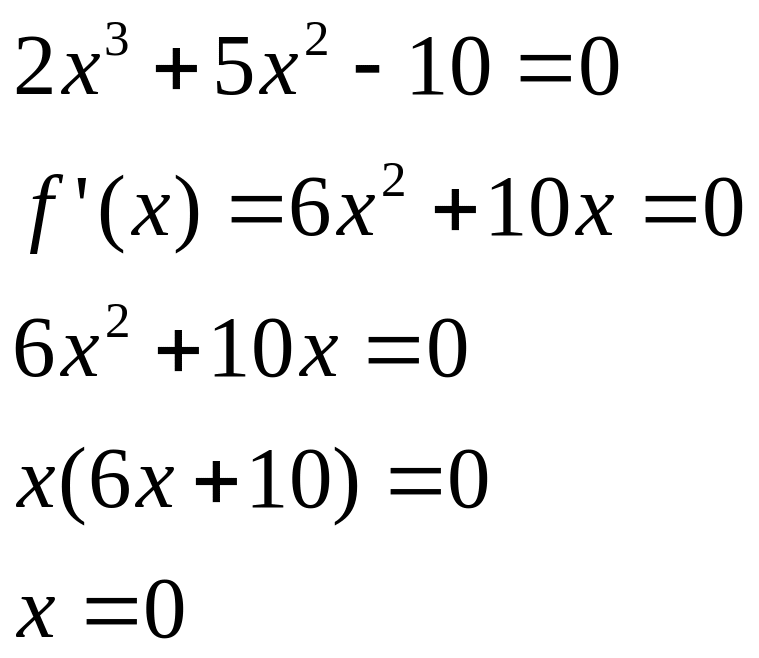


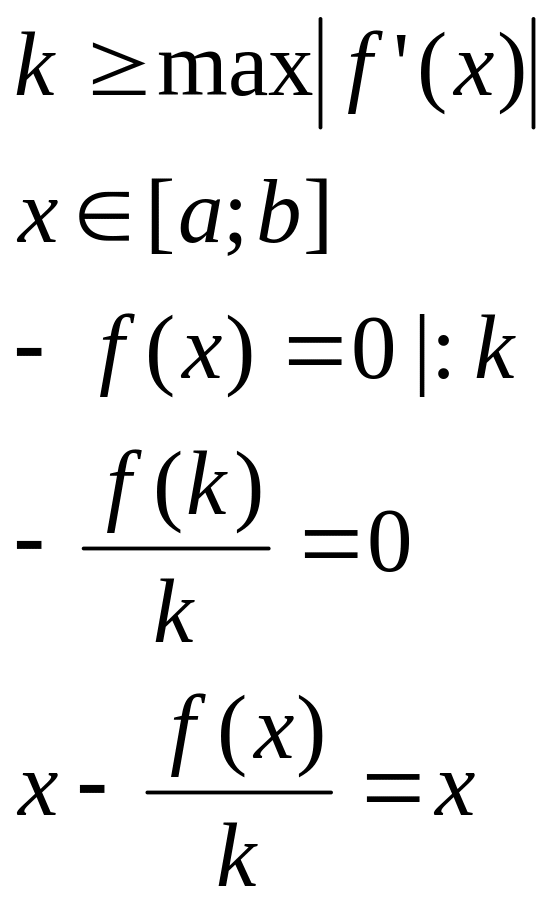
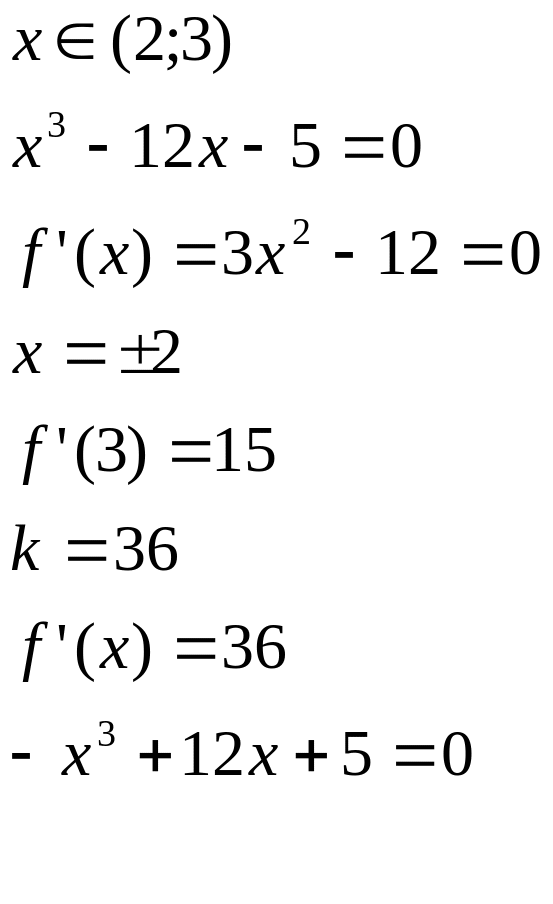

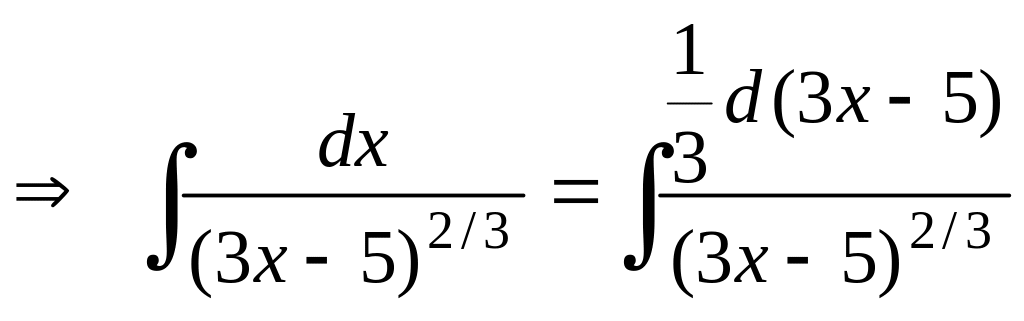 .
.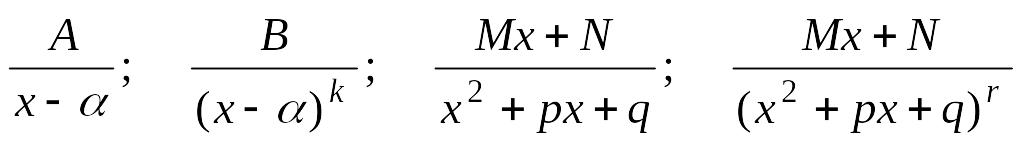 ,
,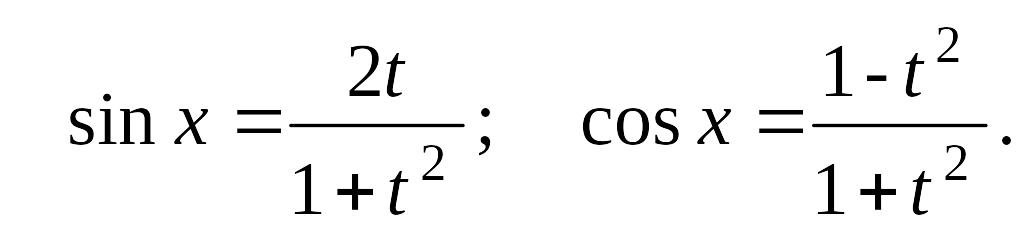
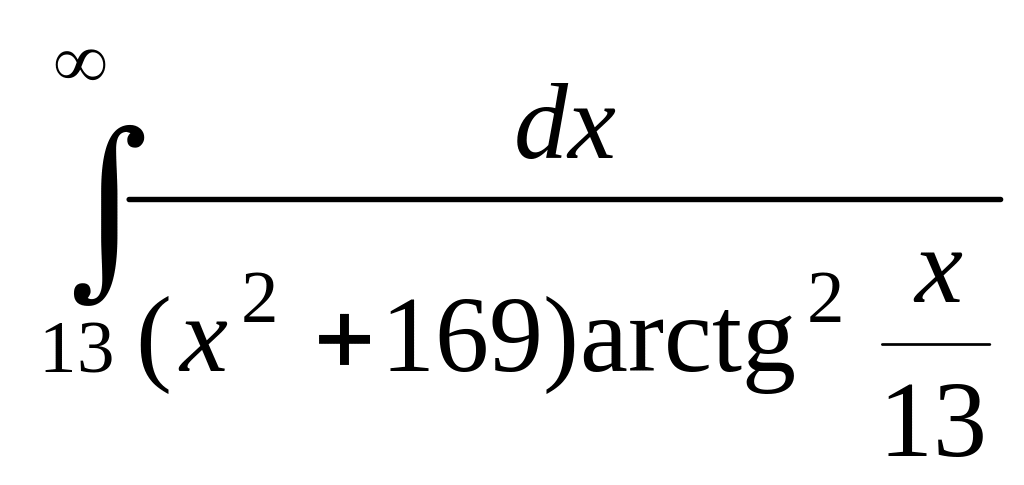 ,
б)
,
б)
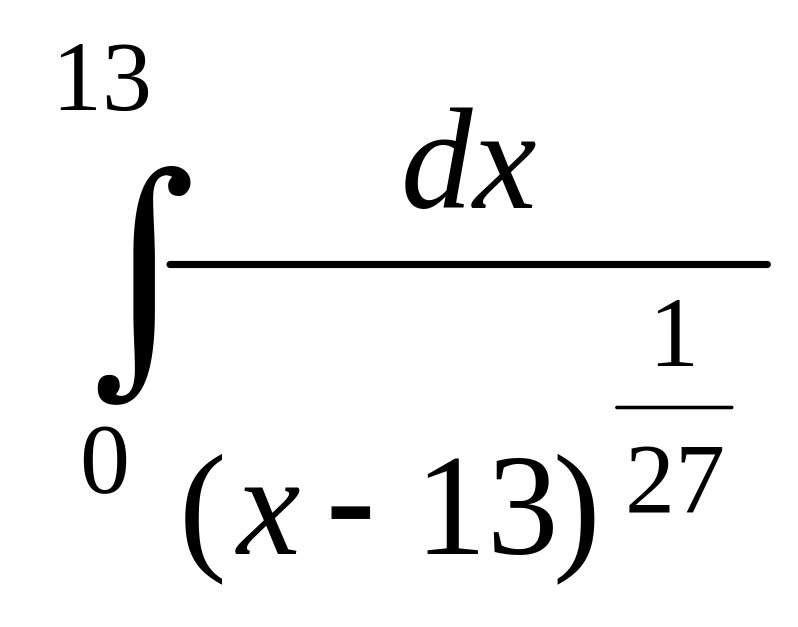 .
.
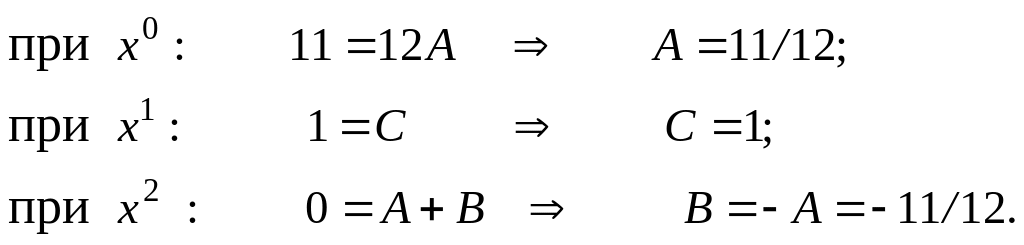
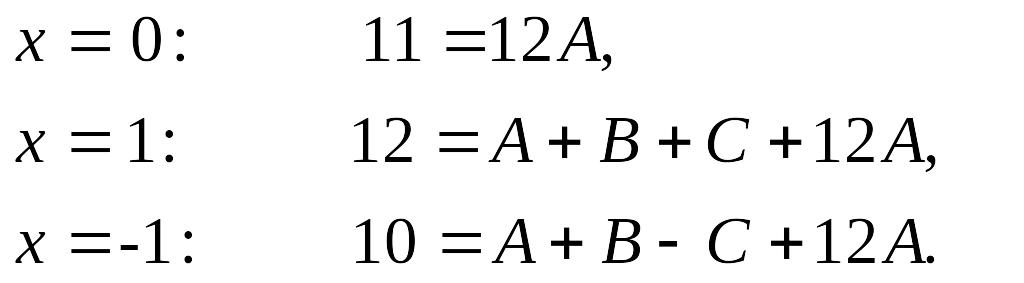
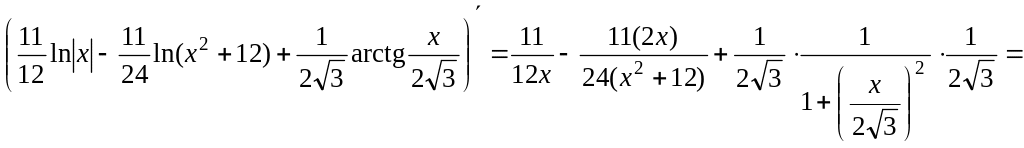
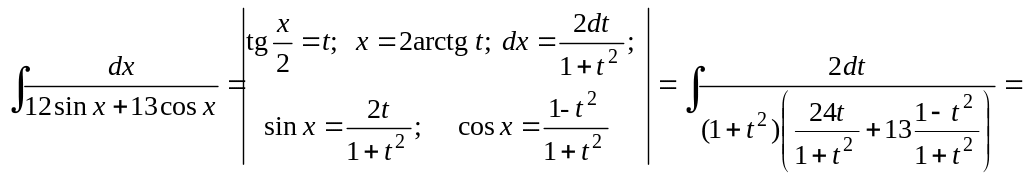
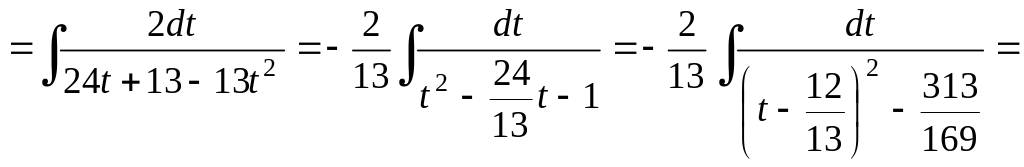
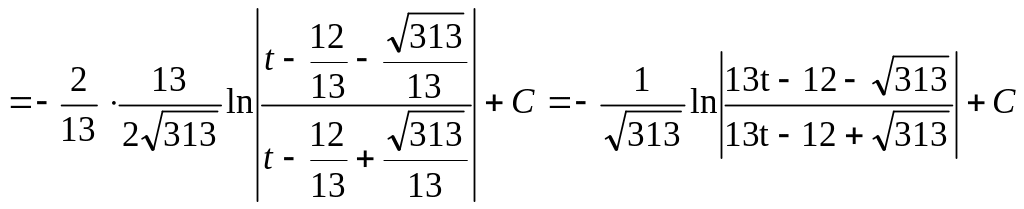 .
.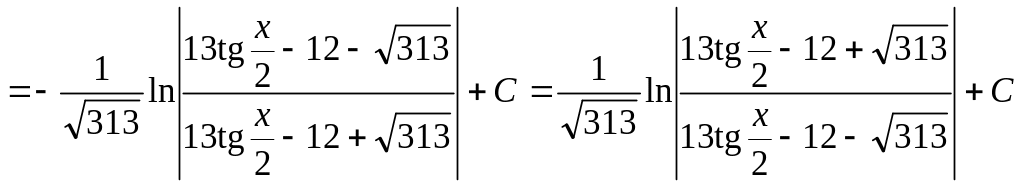 .
. .
.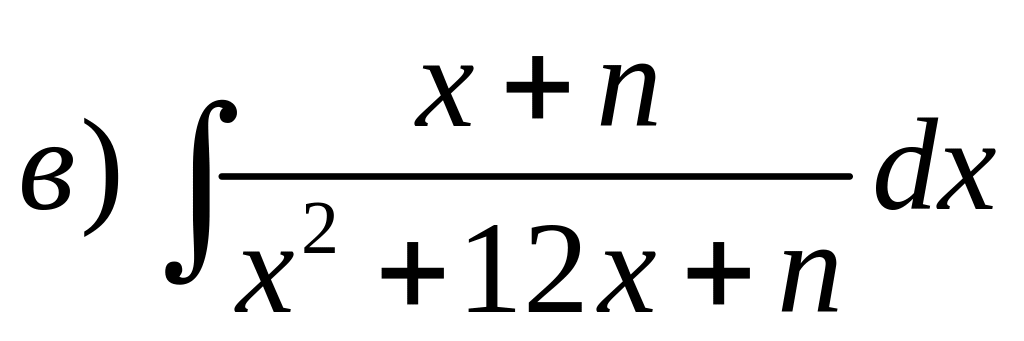 ,
В примерах
правильность полученных результатов
проверить дифференцированием.
,
В примерах
правильность полученных результатов
проверить дифференцированием.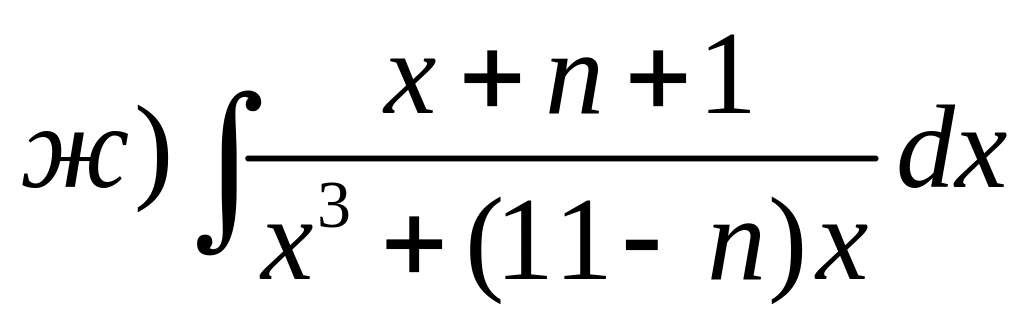 ;
;