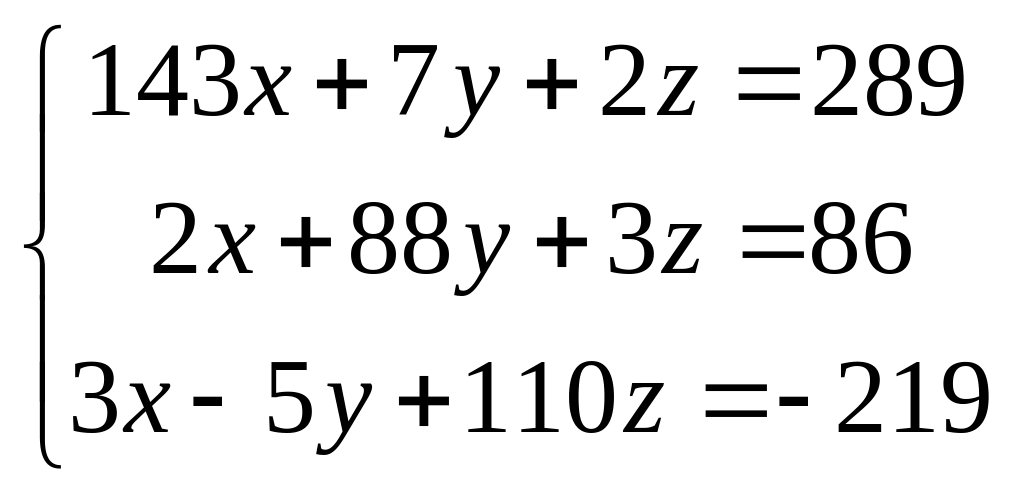- •Аннотация.
- •Содержание.
- •3. Заключение………………………………………………………………………
- •Введение.
- •Основная часть.
- •1.1.Список практических работ.
- •1.2. Ход выполнения практической работы
- •1.3 Критерии оценивания практических работ
- •1.4 Практические работы 1-15. Практическая работа №1
- •Ход работы.
- •Практическая работа №2
- •Ход работы.
- •Решение.
- •Практическая работа №3
- •Ход работы.
- •Контрольные вопросы:
- •Практическая работа №4
- •Ход работы.
- •Практическая работа №5
- •Ход работы.
- •Практическая работа №6
- •Ход работы.
- •Контрольные вопросы:
- •2) Для закрепления теоретического материала и получения прочных знаний решить примеры:
- •Формула Симпсона.
- •2).Контрольные вопросы:
- •Практическая работа №11
- •Ход работы.
- •Практическая работа 12
- •Ход работы.
- •1). Повторение теоретического материала и образцы решения задач:
- •2) Для закрепления теоретического материала и получения прочных знаний
- •Практическая работа 13
- •Дифференциальные уравнения первого порядка.
- •2. Методы решения основных типов дифференциальных уравнений
- •3.Решение задачи Коши для дифференциальных уравнений 1-ого порядка методом Эйлера.
- •Практическая работа 14
- •Методы решения дифференциальных уравнений 2-го порядка, допускающих понижение порядка
- •Практическая работа 15
Ход работы.
По пособию Подольского В.А., Суходского А.М., Мироненко Е.С. «Сборник задач по математике» М.: Высш. шк., 1999г. повторить краткие теоретические сведения и разобрать задачи с решениями: гл.5 стр.78-82,85-101.
Контрольные вопросы:
Виды матриц.
Законы действий над матрицами.
Миноры и алгебраические дополнения.
Основные свойства определителей.
Определение матрицы, обратной данной.
Порядок нахождения матрицы, обратной данной.
для закрепления теоретического материала и получения прочных знаний решить примеры по образцу.
Задание №1.
Даны матрицы
![]() А=
А=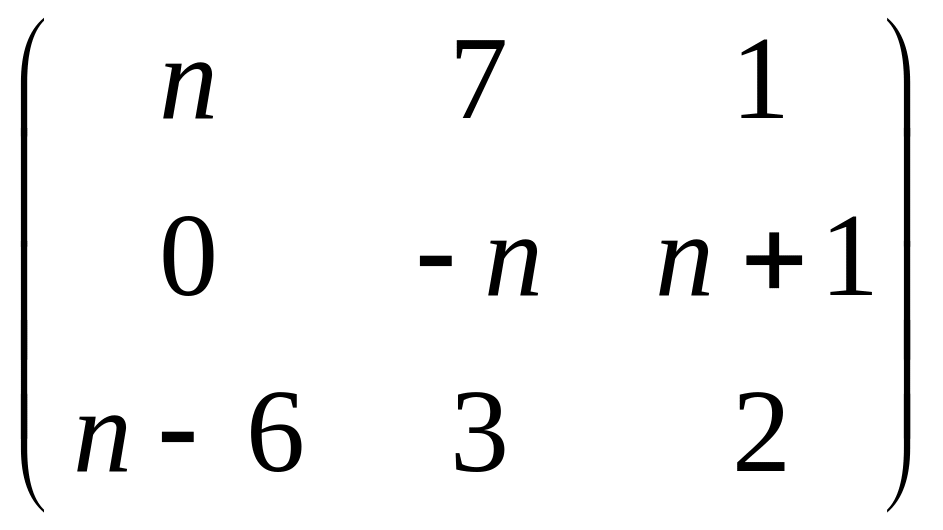 ,
B=
,
B=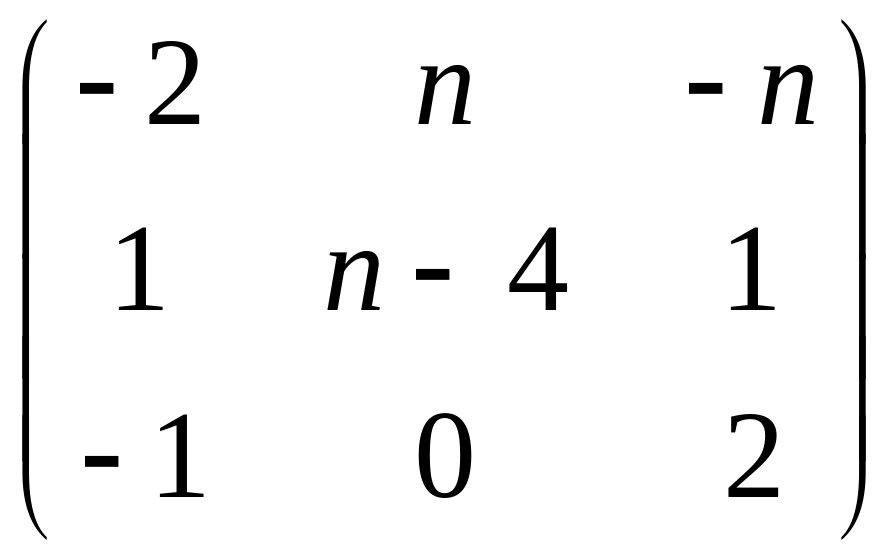 .
Найти матрицу
.
Найти матрицу
![]() .
.
Образец выполнения задания:
Даны матрицы
А=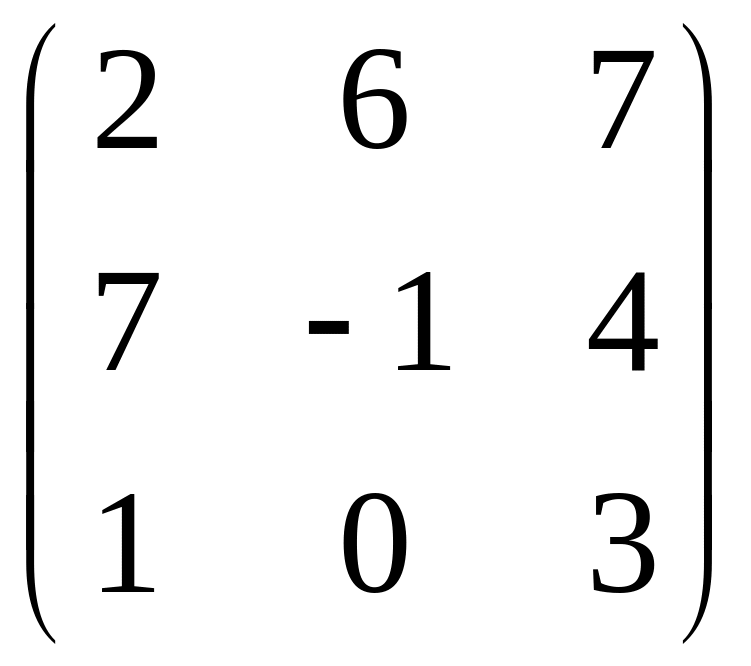 ,
B=
,
B=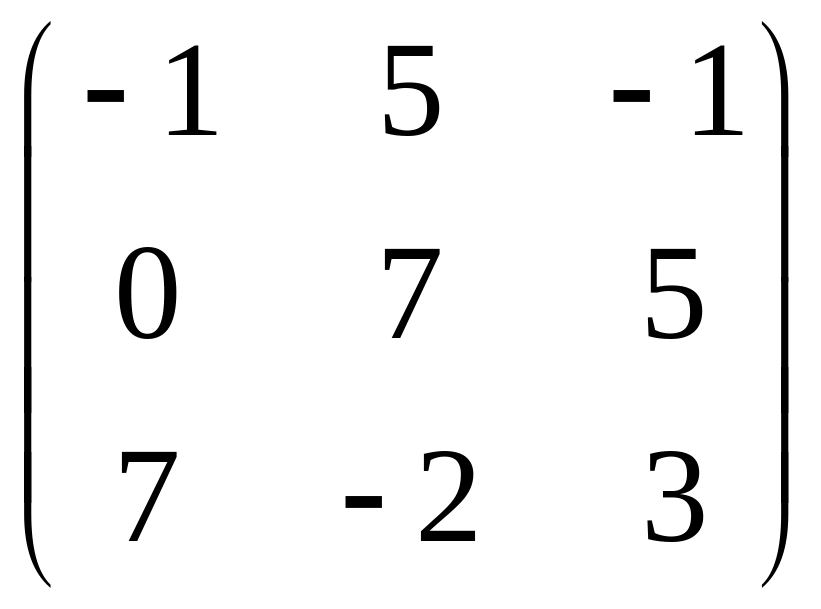 .
Найти матрицу
.
Найти матрицу
![]() .
.
Решение.
2В= .
А-2В=
.
А-2В=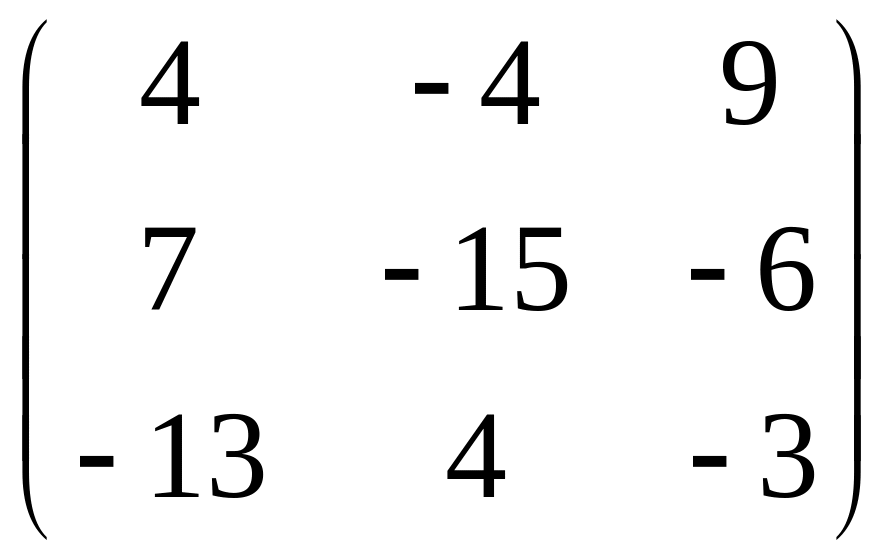 .
.
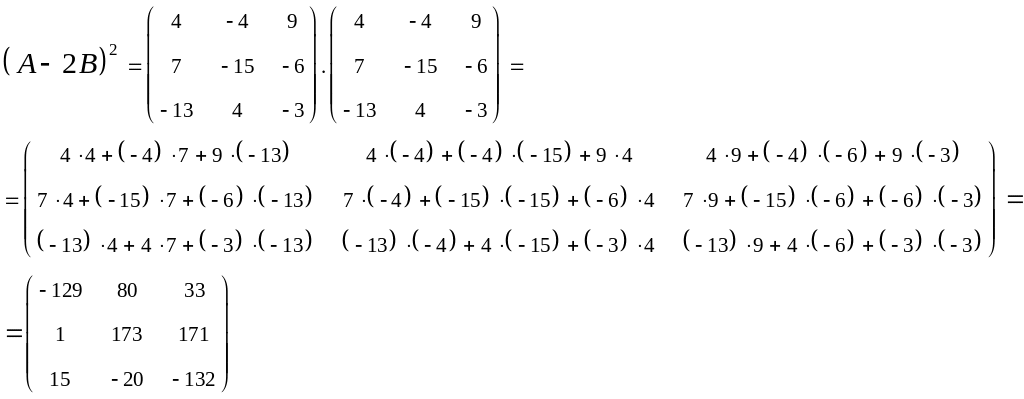
Ответ:
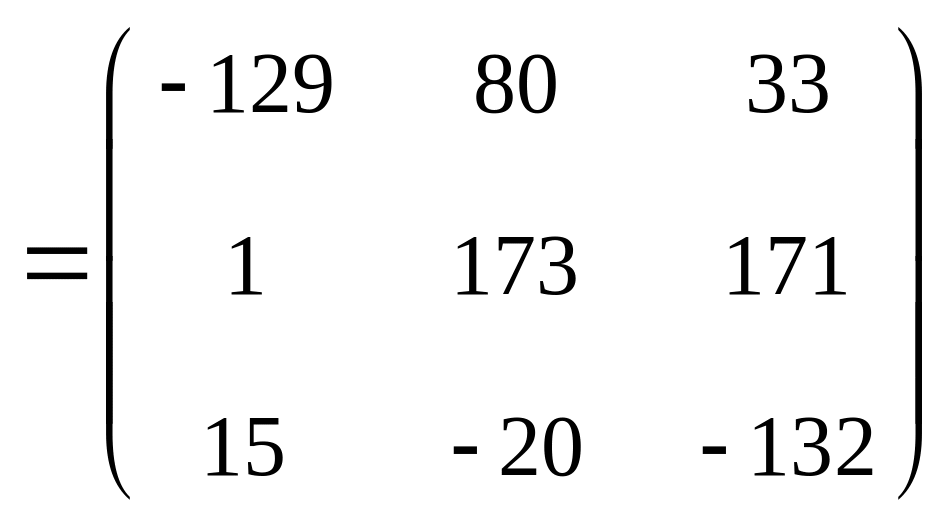
Задание №2:
Вычислить определитель заданной матрицы
способом разложения определителя по элементам строки или столбца:
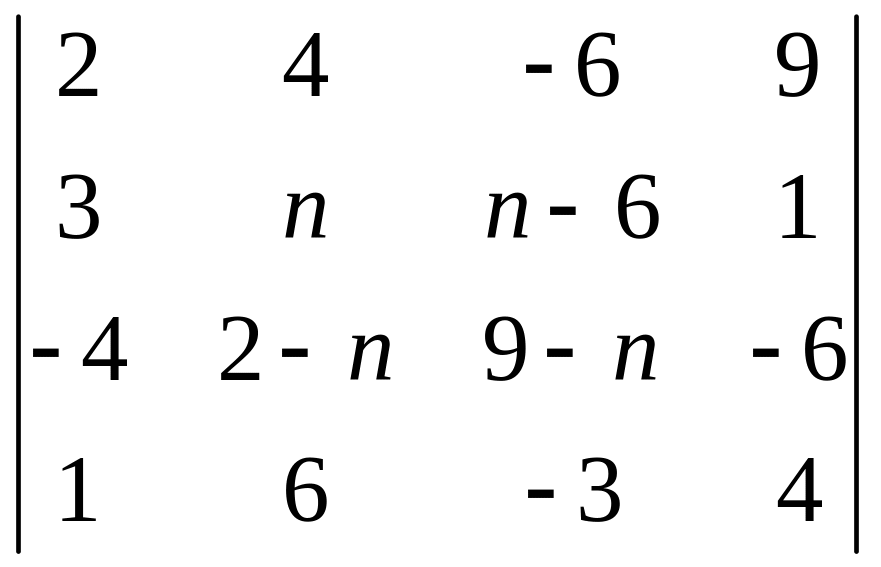
Образец выполнения задания:
Вычислить определитель заданной матрицы
способом разложения определителя по элементам строки или столбца:
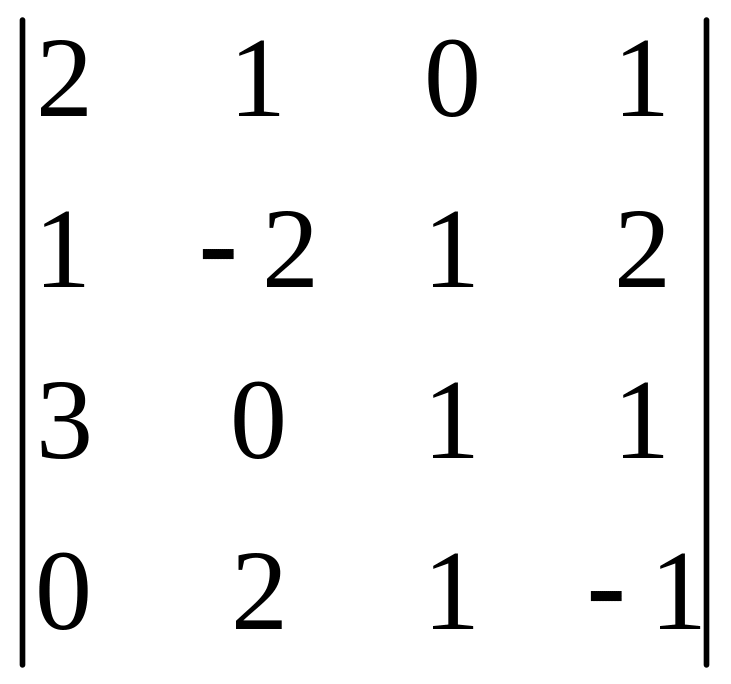
Решение.
Разложим определитель по элементам 1-ого столбца:
=2![]()
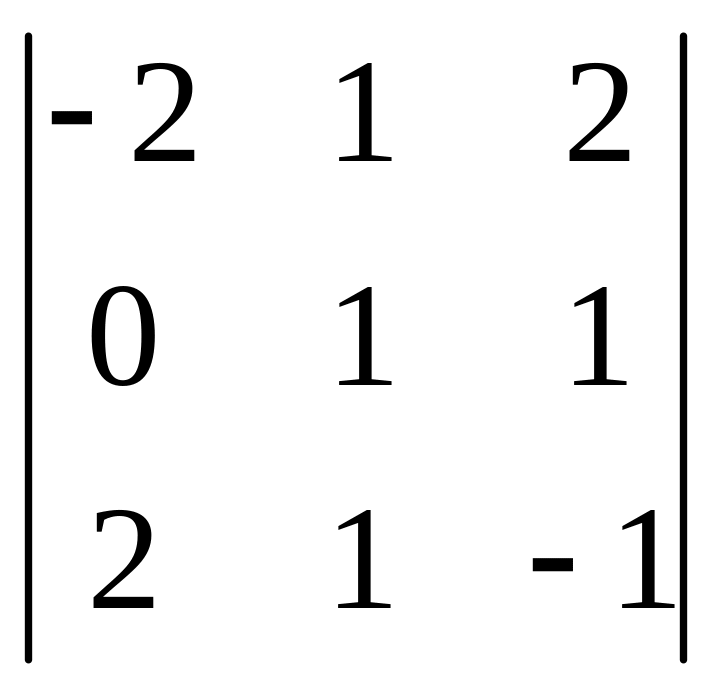 -1
-1
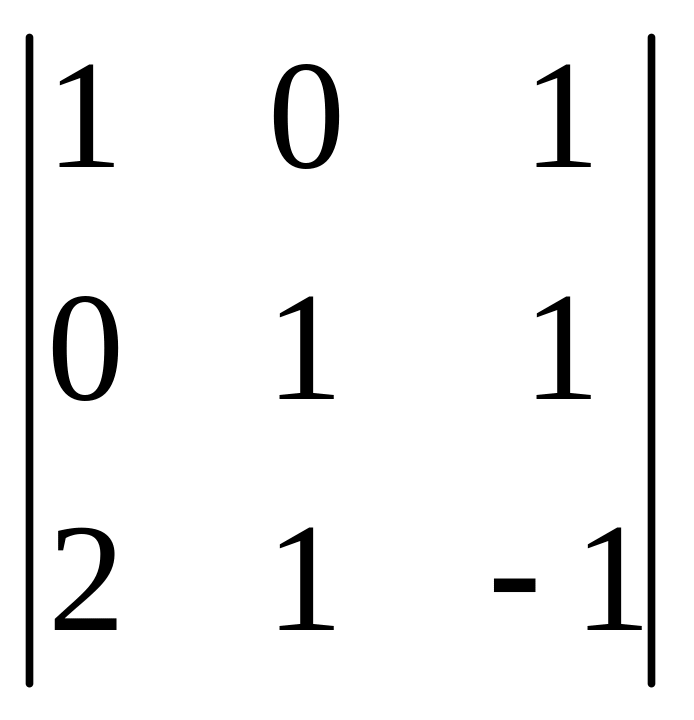 +3
+3
 -0=2(-2
-0=2(-2
![]() -0+2
-0+2
![]() )-1
(1
-0+2
)-1
(1
-0+2
![]() )+3
(1
)+3
(1
![]() +2
+2
![]() +2
+2
![]() )=2
(-2
(-2)+2
(-1))-(-2-2)+
)=2
(-2
(-2)+2
(-1))-(-2-2)+
+3 (-3-2-2)=4+4-21= -13
Задание 3:
Найти матрицу A-1
обратную для матрицы А=
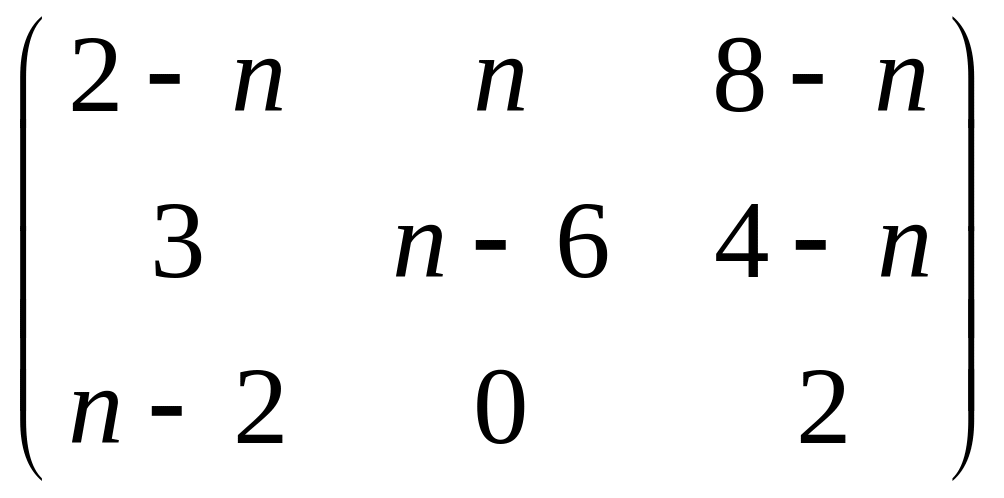 и сделать проверку.
и сделать проверку.
Образец выполнения задания:Найти
матрицу A-1 обратную
для матрицы А=

Решение.
Для нахождения обратной матрицы A-1используется основное соотношение AA-1 = E, где Е – единичная матрица n-го порядка.
находим определитель матрицы:
![]()
 =
-16
=
-16![]() .
.
Т.к.
![]() ,
то матрица имеет обратную.
,
то матрица имеет обратную.
Находим алгебраические дополнения к каждому элементу матрицы:
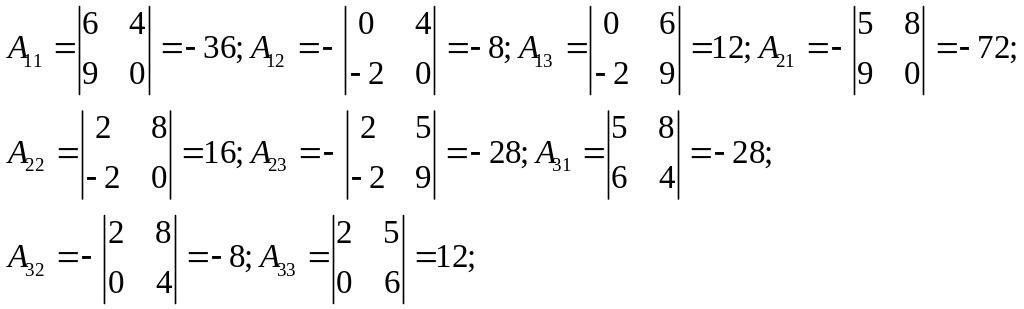
Составляем союзную матрицу:
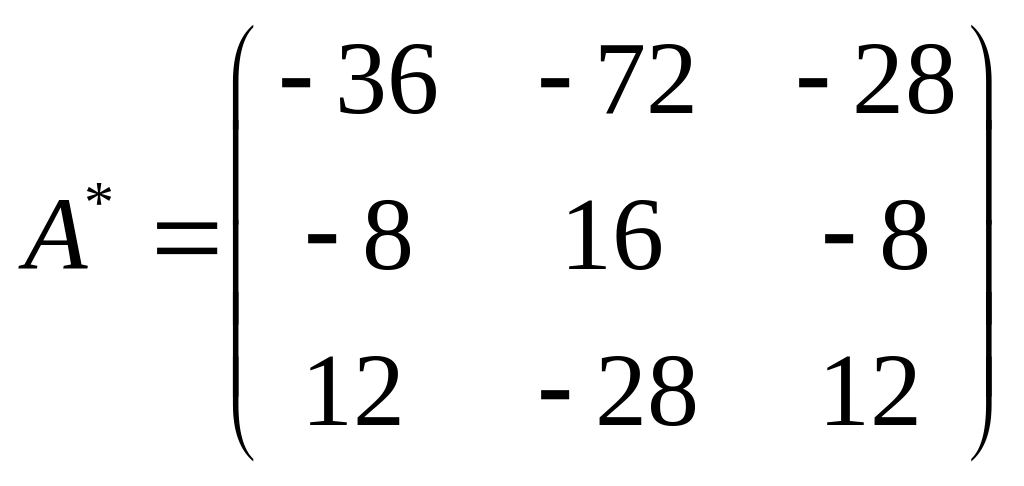
Обратную матрицу находим по формуле:
![]() =
=![]()
 =
=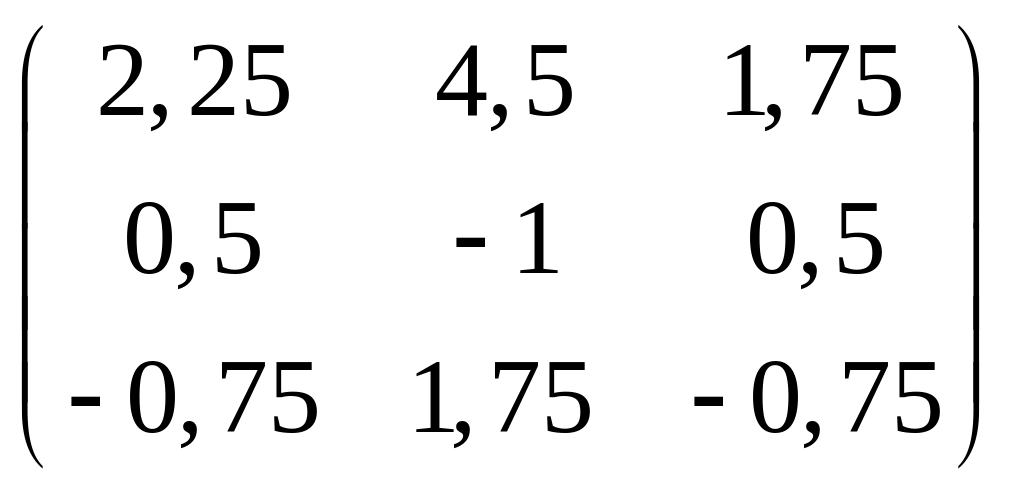
Проверка: AA-1 = E.
Практическая работа №2
Тема: Метод Гаусса. Формулы Крамера.
Цель работы: уметь, используя схему Гаусса, вычислять определители, находить ранг матрицы, исследовать и решать системы линейных уравнений;
уметь решать системы линейных уравнений по формулам Крамера.
Ход работы.
1) По пособию Подольского В.А., Суходского А.М., Мироненко Е.С. «Сборник задач по математике» М.: Высш. шк., 2008 г. повторить краткие теоретические сведения и разобрать задачи с решениями: гл.5 стр.81-84; 102-106.
Контрольные вопросы:
Что называется рангом матрицы?
Чему равен ранг треугольной матрицы?
Элементарные преобразования матриц.
Формулы Крамера.
для закрепления теоретического материала и получения прочных знаний решить примеры по образцу.
Задание 1.
Решить систему уравнений методом Гаусса:
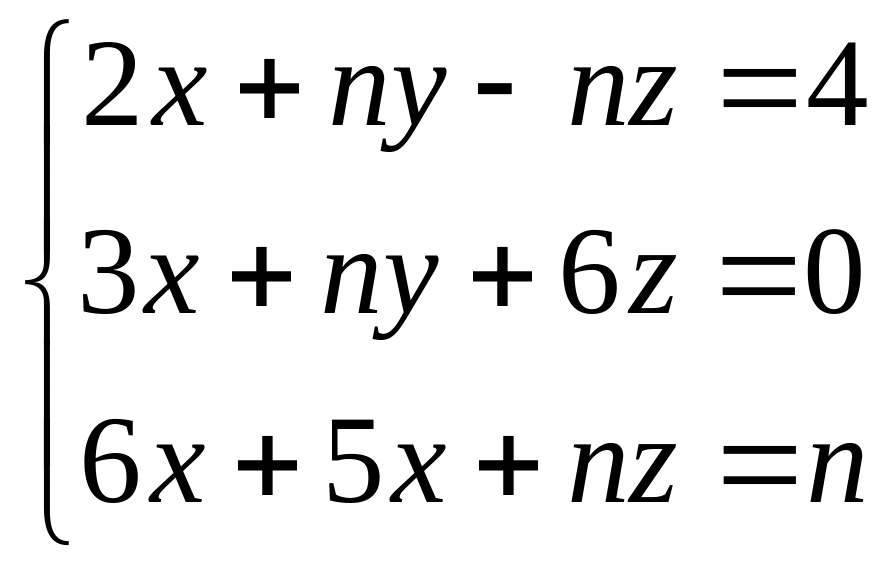
Образец выполнения задания: Решить систему уравнений по схеме Гаусса с точностью до 0,01: