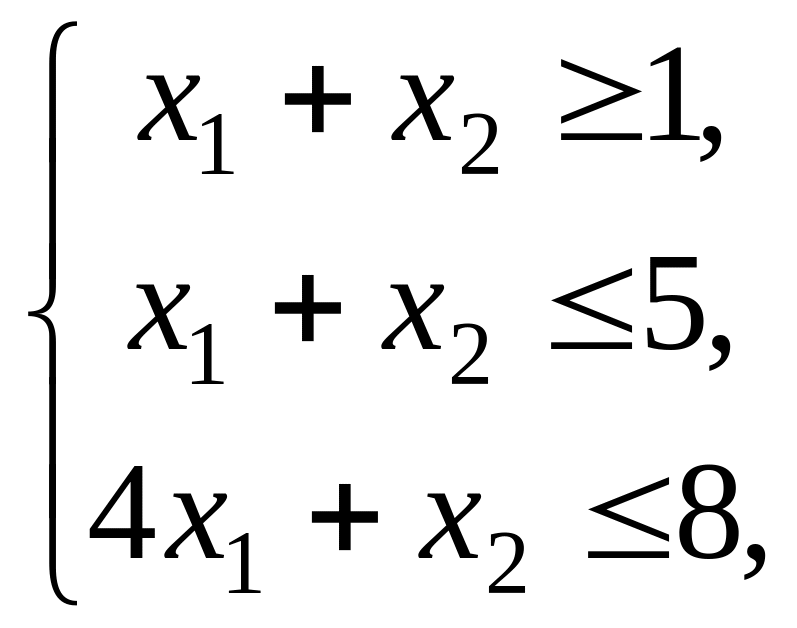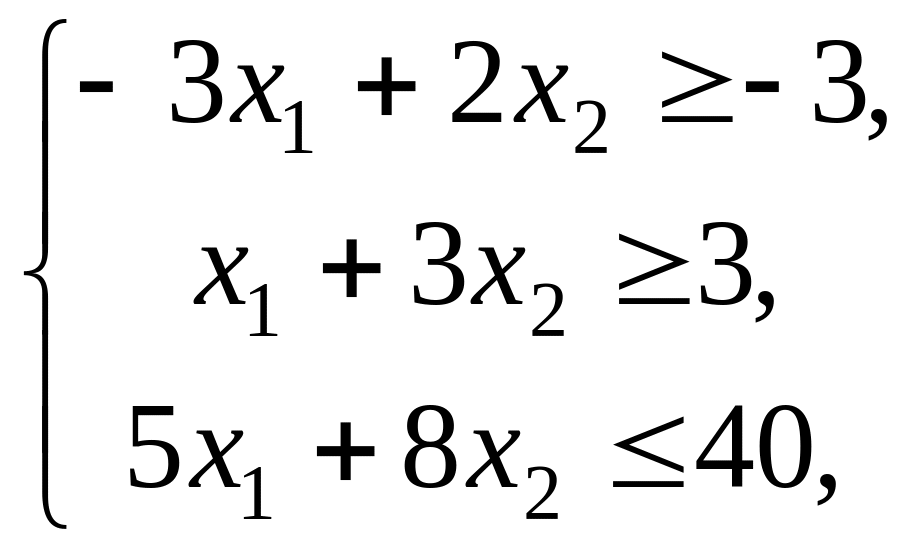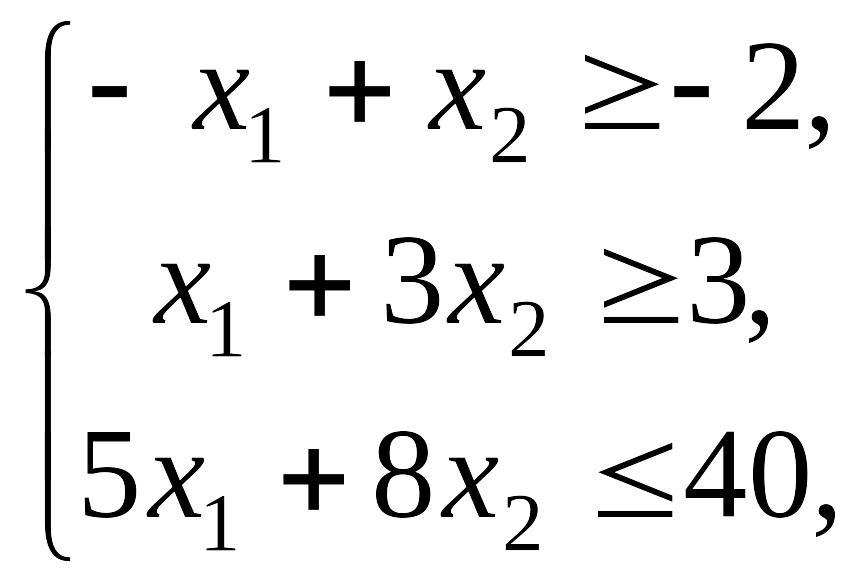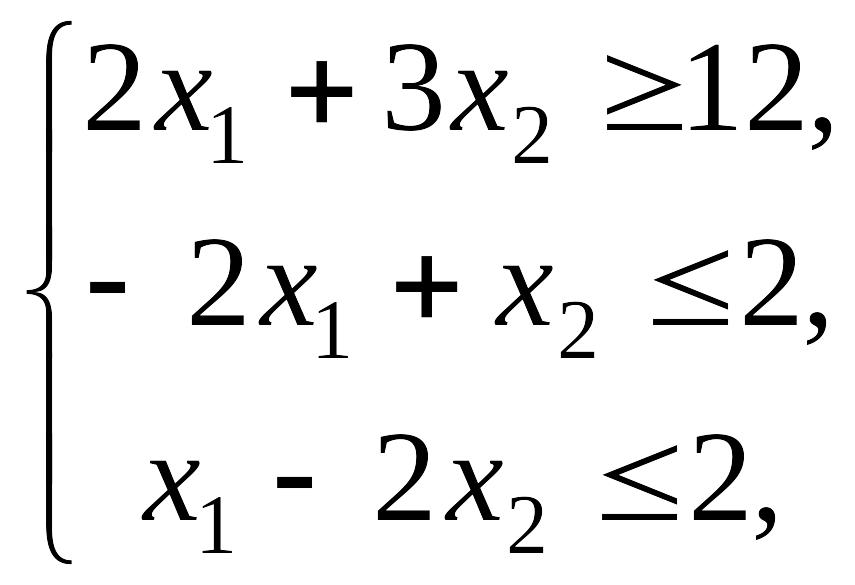5. Исключим теперь из таблицы вспомогательную функцию , искусственную переменную и решим полученную задачу симплекс методом.
|
|
|
|
|
|
|
|
|
1/4 |
1 |
– 1/4 |
0 |
0 |
3 |
– |
|
5/2 |
0 |
1/2 |
1 |
0 |
20 |
40 |
|
– 3/2 |
0 |
1/2* |
0 |
1 |
4 |
8 |
|
13/4 |
0 |
3/4 |
0 |
0 |
-9 |
|
|
– 1/2 |
1 |
0 |
0 |
1/2 |
5 |
– |
|
4* |
0 |
0 |
1 |
–1 |
16 |
4 |
|
– 3 |
0 |
1 |
0 |
2 |
8 |
– |
|
11/2 |
0 |
0 |
0 |
– 3/2 |
–15 |
|
|
0 |
1 |
0 |
1/8 |
3/8 |
7 |
|
|
1 |
0 |
0 |
1/4 |
– 1/4 |
4 |
|
|
0 |
0 |
1 |
3/4 |
11/4 |
20 |
|
|
0 |
0 |
0 |
–11/8 |
– 1/8 |
-37 |
|
Из последней таблицы мы получим оптимальное решение канонической задачи (25):
,
,
,
,
,
,
а следовательно функция принимает свое максимальное на множестве значение равное в точке с координатами ; .
6. Двойственная задача к искомой задаче будет иметь вид:
,
,
или в матричной форме:
,
,
с матрицами (24) и матрицей
.
7. Из последней симплекс таблицы мы найдем значения двойственных переменных:
,
,
Подставим эти числа в ограничения двойственной задачи и целевую функцию:
,
,
.
Так как выполнены все условия теоремы двойственности, то найденное решение:
,
,
,
будет оптимальным решением двойственной задачи.
Варианты заданий
1
|
2
|
3
|
4
|
5
|
6
|
7 ,
|
8 ,
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18 ,
|
19 ,
|
20
|
21
|
22
|
23 ,
|
24
|
25
|
26
|
27
|
28
|
29
|
30 ,
|
31 ,
|
32
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,