5. Метод кусочно-линейной аппроксимации при

расчете переходного процесса в нелинейном элементе.

В соответствии с пунктом 5 и данными карточки 1 задания исходная схема преобразовывается в схему рис. 4, в которой емкость C₃ не линейна.

Существует достаточно много методов расчета переходных процессов в нелинейных цепях. В данном задании предполагается выполнить расчет методом кусочно-линейной аппроксимации применительно к схемам с одним нелинейным элементом-индуктивностью или емкостью.

Нелинейный конденсатор характеризуется нелинейной кулон-вольтной характеристикой , где Q – заряд емкости; U_C – напряжение на емкости. Значение емкости определяется соотношением . Нелинейная катушка индуктивности характеризуется нелинейной вебер-амперной характеристикой , где ψ – потокосцепление, i_L – ток в катушке. Значение индуктивности определяется отношением .

Сущность метода кусочно линейной аппроксимации состоит в замене характеристики нелинейного элемента отрезками прямых и нахождении для каждого из них переходной функции искомого параметра. Для припасовывания решений, соответствующих отдельным линейным участком, на основании законов коммутации находят условия связи между постоянными интегрировании.

Рекомендуемый порядок расчета:

1. Исследуемую схему с помощью эквивалентных преобразований представить в виде последовательного соединения эквивалентного источника эдс и нелинейного элемента (рис. 15), где и - эквивалентные параметры двухполюсника относительно зажимов нелинейного элемента.

2. Построить по данным карточки характеристику нелинейного элемента (НЭ) и аппроксимировать ее двумя прямыми (рис. 16). Один из возможных вариантов аппроксимации состоит в том, что одна прямая проводится через начало координат касательно к характеристике, а вторая через точку принужденных значений касательно к характеристике в случае нелинейной индуктивности или через точку касательно к характеристике в случае нелинейной емкости (рис. 16).

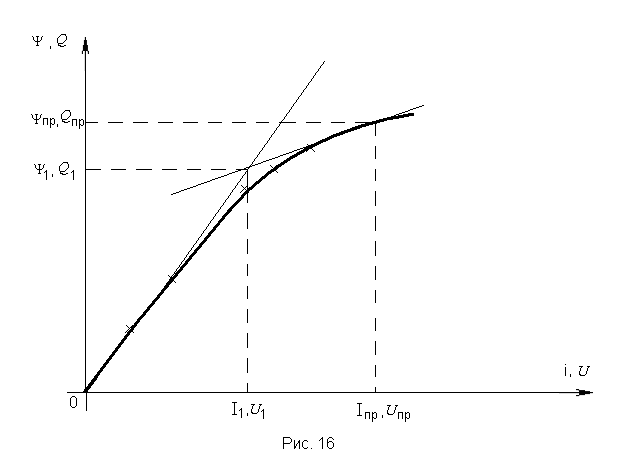
3. Для каждого линейного участка аппроксимированной характеристики найти значение

параметра НЭ, т.е. определить или .

Таким образом, для случая, когда нелинейным элементом является, например, емкость, схема рис.15 рассчитывается дважды. Один раз с линейной емкостью (рис.15 а), соответствующей первой прямой, и второй раз с линейной емкостью (рис.15 б), соответствующей второй прямой.

4. Произвести расчет переходного процесса для схем рис.15 а и рис.15 б любым способом

(например, операторным) и, записав аналитическое выражение искомой переходной функции тока (напряжение), припасовать решения в точке . Построить зависимость или от времени.

Занести в таблицу результатов расчета, изображенную на титульном листе задания, параметры эквивалентного генератора относительно зажимов нелинейного элемента и зависимость искомой переходной величины в функции времени.

5. Частотный метод (метод трапеции)

В задании предлагается в схеме, имеющей конфигурацию по пункту 4 (при этом оставить другой, по сравнению с пунктом 4, реактивный элемент), определить ток в индуктивности или напряжение на емкости при включении схемы на постоянную эдс.

Так как имеют место нулевые независимые начальные условия,

то , ,

где , - переходная проводимость, переходная функция по напряжению.

Применяя преобразование Фурье, учитывая нулевые начальные условия, можно показать:

, ,

где - вещественная часть частотных спектров проводимости и передаточной функции.

Для расчета интегралов используется метод трапеции. Зная или , по формулам (17) находим или .

Определение и

Исходные схемы показаны на рис.17, схемы для частотных спектров- на рис.18 (а - для ; б – для ).

Вид и не зависит от вида , поэтому удобно в схему вместо поставить единичную эдс, частотный спектр которой равен

Очевидно, что в рассматриваемых схемах для частотных спектров при нулевых начальных условиях:

, . (19)

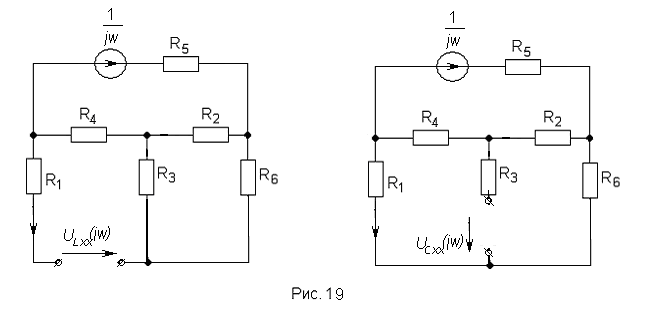
Из выражения (19) следует, что для нахождения и необходимо рассчитать для частотных спектров и определить соответственно или . Расчет схем для частотных спектров проводится любым методом расчета установившихся режимов. Показанные схемы на рис.18 удобно рассчитать методом эквивалентного генератора относительно зажимов или . Схемы для определения показаны на рис.19.

В результате расчета заданных схем (например, методом контурных токов) получим, что , , где . Это объясняется тем, что схемы по рис.19 состоят из чисто активных сопротивлений. Разумеется, величина будет различна для обеих схем.

Далее, определяя входное сопротивление относительно зажимов или , получим, что , т.е. является чисто активным. Зная и , находим:

, (20)

Подставляя полученные значения в выражения (19), имеем:

(21)

Для выделения вещественных частей и преобразуем выражение (21):

(22)

Из формулы (22) следует:

, . (23)

Построение и аппроксимация или

1.Строим зависимость или . Для этого задаемся рядом значений от 0 до , пока отношение ; станет 0,25. Характерный вид зависимостей , показан на рис.20. Эта кривая асимптотически приближается к оси при . Без большой потери точности допустимо ограничиться расчетом , на интервале , на рис.20 .

2.На указанном интервале заменяем полученную зависимость отрезками ломаной прямой “абвг”. Чем больше отрезков , тем выше точность. В задании ограничиться тремя отрезками.

3.Заменяем на каждом отрезке ординаты ломаной прямой суммой ординат трапеции. Так, на участке ”гв” ломаная прямая заменена трапецией с высотой , с характерными частотами и . На участке “вб”- в основном суммой двух трапеций (первой и второй) так, что в интервале частот сумма ординат . Здесь обозначает приближенное значение на втором участке. На третьем участке – “ба”ломаная прямая аппроксимируется суммой трех трапеций.

Составляется таблица, показанная на рис.20.

Расчет или

Представление или в виде суммы трапеций приводит к тому, что интегралы (18) переходят в сумму интегралов, каждый из которых дает -ю составляющую или от действий й трапеции. Искомые значения , будут равны:

,

, ,

где - переходная функция, значения которой табулированы и приведены в приложении.

Расчет или удобно вести в форме табл.3.Для расчета или задается ряд значений . Удобно взять значения приведенные в столбце 1. Под понимается : для схемы с ; для схемы с

Значения находятся из таблицы приложения. Столбцы 8,9,10,11 считаются соответственно или для , . Зная или (столбец 11), находим или по (17). Строим полученную кривую.

Заполнить таблицу результатов расчета, помещенную на титульном листе задания.

1	2	3	4	5	6	7	8	9	10	11
t (C)	τ1=ω01·t	τ2=ω02·t	τ3=ω03·t	η1·(τ1,x1)	η2·(τ2,x2)	η3·(τ3,x3)	g1**=η1·P01	g2**=η2·P02	g3**=η3·P03	gL(t)**=g1+g2+g3
0	0	0	0	0*	0*	0*	0	0	0	0
0.1τp				*	*	*
0.5τp					и т.д.
τp
1.5τp
2τp
3τp
4τp
5τp

Таблица 3

* - Находятся из приложения

** - Для расчета K_C(t) считаются соответственно K_C1, K_C2, K_C3, и K_C(t).