3.1.2 Физическая интерпретация формулы Даламбера

Предположим, что в начальный момент струна покоилась, тогда формула Даламбера будет иметь вид

.

Из полученной формулы следует, что первоначальное возмущение распадается на две волны, бегущие в разные стороны со скоростями . Причем первому слагаемому отвечает волна, бегущая вправо, а второму слагаемому – влево (рисунок 4).

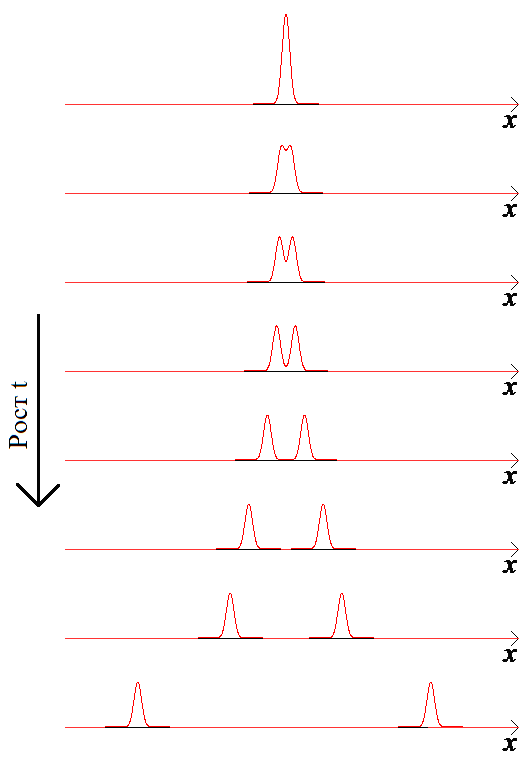
Рисунок 4

3.2 Смешанная задача для свободных колебаний струны с закрепленными концами

В данном случае имеем задачу

УЧП: ;

НУ: ;

;

ГУ: , .

Решим задачу методом Фурье (методом разделения переменных). Для этого будем искать ее решение в виде

.

Подставив это решение в УЧП, получим

.

Разделим полученное уравнение на .

. (6)

Выражение не зависит от переменной , а выражение не зависит от переменной . Тогда из того, что эти выражения тождественно равны, следует, что они не зависят ни от , ни от . Тогда их можно положить равными константе .

Из соотношения (6) получаем два обыкновенных дифференциальных уравнения:

, (7)

. (8)

Теперь рассмотрим граничные условия:

1) ;

2) .

Так как не может тождественно равняться 0 (в противном случае имеем: ‑ струна неподвижна), то тогда из граничных условий следует, что и .

Объединив два полученных условия с уравнением (8), получим так называемую задачу Штурма-Лиувилля

(9)

1. Рассмотрим случай . Тогда положив, будем иметь задачу

Для данного ОДУ характеристическое уравнение будет иметь вид

.

Так как его корни равны и , то тогда общим решением ОДУ является

.

Используем условия и :

1) ;

2) .

Таким образом, получили однородную систему линейных алгебраических уравнений

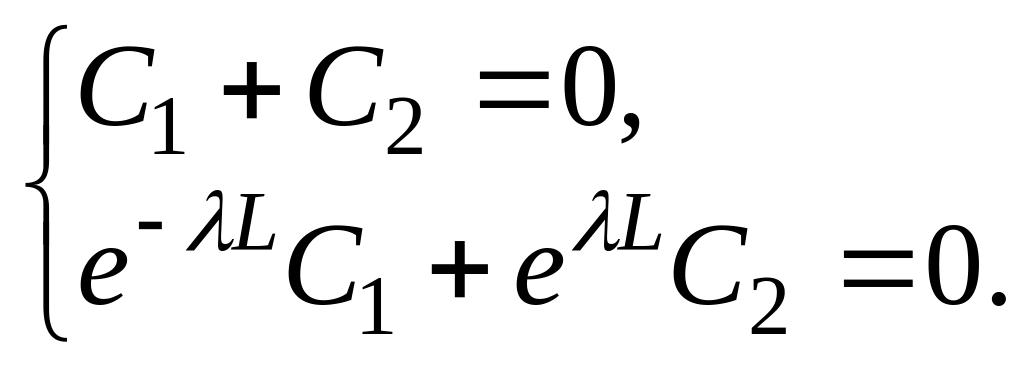
Определитель этой системы равен

,

так как и .

Так как , то однородная система имеет единственное нулевое решение и .

Тогда и ‑ струна неподвижна.

Отсюда следует, что случай не может соответствовать колеблющейся струне.

2. Рассмотрим случай . Тогда будем иметь задачу

Для данного ОДУ характеристическое уравнение будет иметь вид

.

Так как оно имеет корень второй кратности , то тогда общим решением ОДУ является

.

Используем условия и :

1) ;

2) .

Таким образом, получили систему уравнений

Так как , то система имеет единственное нулевое решение и .

Тогда и ‑ струна неподвижна.

Отсюда следует, что случай также не может соответствовать колеблющейся струне.

3. Рассмотрим случай . Тогда положив, будем иметь задачу

Для данного ОДУ характеристическое уравнение будет иметь вид

.

Так как его корни , то тогда общим решением ОДУ является

.

Используя условие , получим

.

Тогда

.

Используя условие , получим

.

Отсюда или .

Случай следует исключить, так как тогда и ‑ струна неподвижна.

Из имеем , где .

Тогда .

Из и следует, что .

Получаем, что данная задача Штурма-Лиувилля только при найденных значениях имеет ненулевые решения . Они для каждого значения единственны с точностью до постоянного множителя .

Числа называются собственными значениями задачи Штурма-Лиувилля, а функции ‑ собственными функциями задачи Штурма-Лиувилля.

Теперь рассмотрим ОДУ (7). С учетом найденного значения , будем иметь ОДУ

.

Для данного ОДУ характеристическое уравнение будет иметь вид

.

Так как его корни , то тогда общим решением ОДУ является

.

Так как полученное решение зависит от , то в дальнейшем будем использовать обозначения . Кроме того, произвольные постоянные для каждого значения могут быть различны, поэтому выберем для них обозначения и .

Тогда общее решение ОДУ (7) примет вид

.

Получили решения УЧП вида

.

Так как данное УЧП является линейным, то можно предположить, что также будет являться его решением и ряд

. (10)

Следует отметить, что это решение удовлетворяет ГУ исходной задачи.

Для нахождения коэффициентов и используем НУ.

Применив первое НУ, будем иметь

.

Получили разложение в ряд Фурье по синусам на отрезке функции . Тогда из теории рядов Фурье имеем

.

Применим второе НУ:

,

.

Получили разложение в ряд Фурье по синусам на отрезке функции . Тогда

, .

Таким образом, решение рассматриваемой задачи следует проводить по схеме: