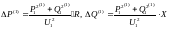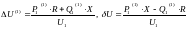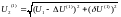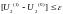12. Связь между напряжениями и мощностями элементов электрической сети (основное соотношение электрических расчётов).

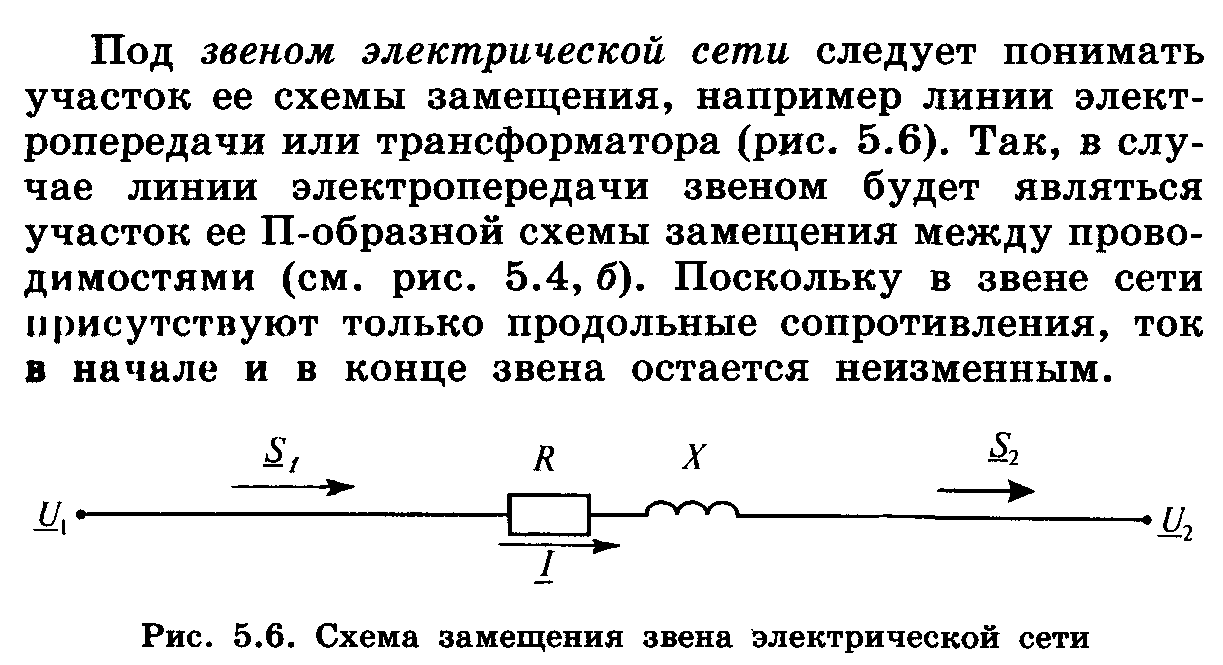
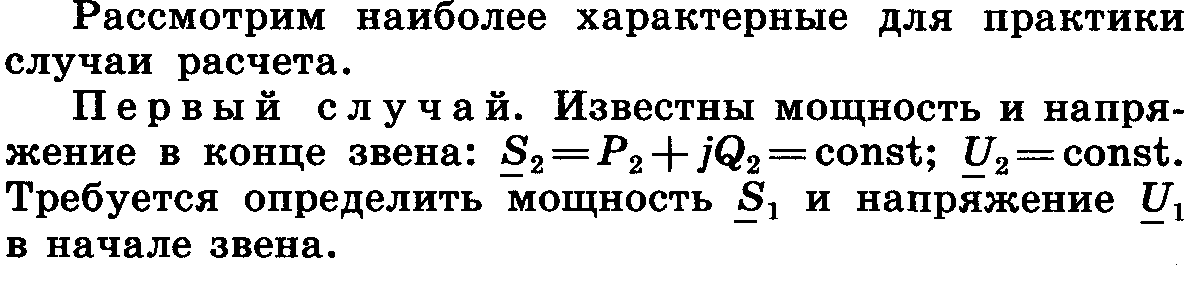
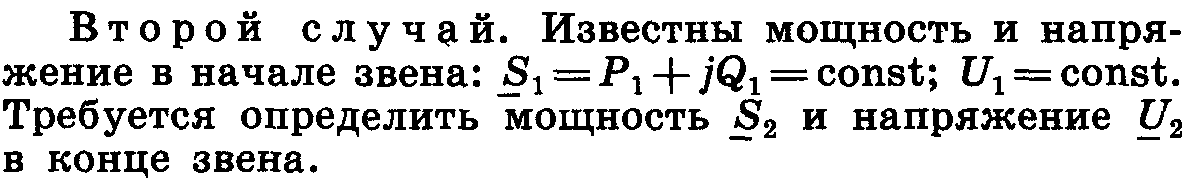
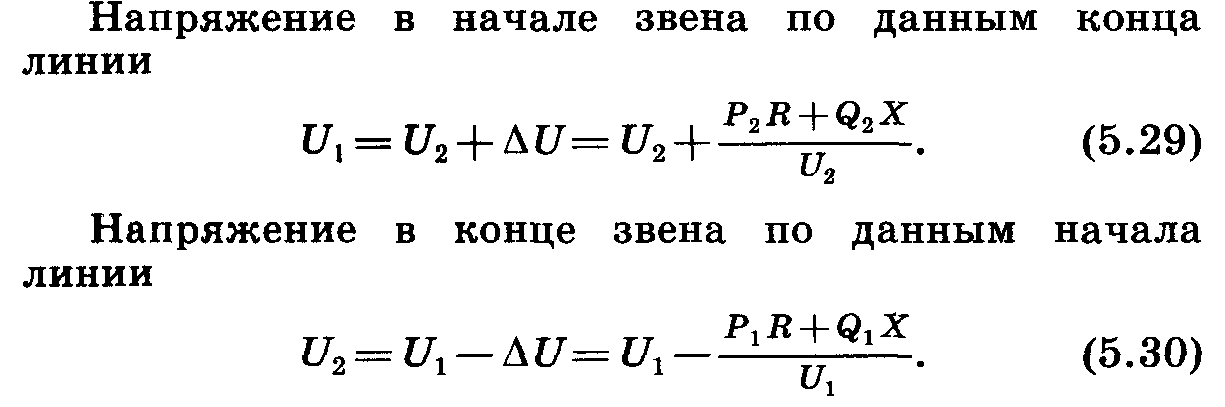
Существует также третий случай, когда известна мощность в конце и напряжение в начале. В таком случае применяют метод последовательных приближений.

13. Падение и потеря напряжения.

Падение напряжения – геометрическая (векторная) разность между комплексами напряжений начала и конца линий (отрезок АВ на рисунке).

Продольной составляющей падения напряжения называют проекцию падения напряжения на действительную ось (отрезок АС)

Поперечная составляющая падения напряжения - это проекция падения напряжения на мнимую ось (отрезок ВС).

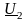
Часто используют понятие потеря напряжения – это алгебраическая разность между модулями напряжений начала и конца линии. Если поперечная составляющая мала, то можно приближенно считать, что потеря напряжения равна продольной составляющей падения напряжения (пренебрегая также отрезком ВС, который в таком случае также незначителен).

14. Определение напряжения и мощности в конце элемента сети по данным начала.

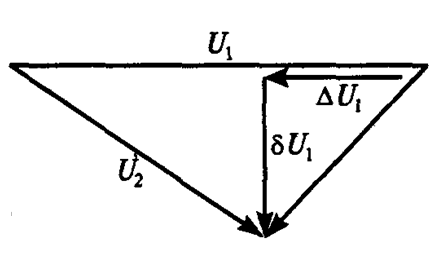
Векторная диаграмма напряжений для данного примера

15. Расчет режима линии электропередачи.

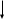
P₁^’-jQ₁^’

U₁

P₁-jQ₁

R

X

U₂

P₂-jQ₂

P_н-jQ_н

∆P_к2+j∆Q_В2

∆P_к1+j∆Q_В1

∆P_к1 – Есть функция от U₁

∆P_к2 – Есть функция от U₂

“+” перед ∆Q_В2 и ∆Q_В1 генерация

При расчёте ЛЭП возможны три случая:

1. Задана P_н-jQ_н, U₂ Найти P₁^’-jQ₁^’, U₁

2. Задана P₁^’-jQ₁^’, U₁ Найти P_н-jQ_н, U₂

3. Задана P_н-jQ_н, U₁ Найти P₁^’-jQ₁^’, U₂

Случай 1

P_н-jQ_н =const U₂=const

Найти

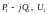
1. ∆P_к2=U²₂*G/2; ∆Q_В2= U²₂*B/2

2. P₂-jQ₂=( P_н-jQ_н)+( ∆P_к2+j∆Q_В2)= (P_н+∆P_к2)-j(Q_н-∆Q_В2)

3. 

4. 

5. 

6. 

7. 

8. 

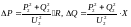
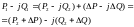
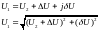
Случай 2

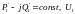=const

Найти P_н-jQ_н ,U₂

1. ∆P_к1=U²₁*G/2; ∆Q_В1= U²₁*B/2

2. P₁-jQ₁=( P₁^’-jQ₁^’)-( ∆P_к1+j∆Q_В1)= (P₁¹-∆P_к1)-j(Q₁^’+∆Q_В1)

3. 

4. 

5. 

6. 

7. 

8. 

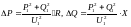
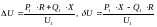
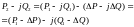
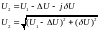
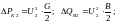
Случай 3

=const

Найти

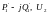
Этот случай наиболее распространен расчёт ведется в 2 этапа:

1 этап. От конца к началу. Во всех узлах 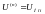(принимается одинаковое начальное значение приближения напряжения равное, например, номинальному)

1. ∆P_к2⁽¹⁾=U²₂⁽⁰⁾*G/2; ∆Q_В2⁽¹⁾= U²₂⁽⁰⁾*B/2

2. P₂⁽¹⁾-jQ₂⁽¹⁾=( P_н-jQ_н)+( ∆P_к2⁽¹⁾+j∆Q_В2⁽¹⁾)= (P_н+∆P_к2⁽¹⁾)-j(Q_н-∆Q_В2⁽¹⁾)

3. 

4. 

5. 

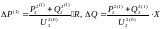
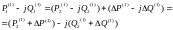
2 этап. У нас даны U₁=const, 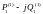-- рассчитали.

1. 

2. 

3. 

4. 

5. 

Нет (продолжение процедуры) Да (конец расчёта)

16. Учет трансформаторов при расчете режима электрической сети.

Одним из основных элементов любой электрической сети яв­ляются трансформаторы. Учитывая, что при расчете режима сети нагрузки потребителей задаются, как правило, со стороны обмоток низших напряжений трансформаторных подстанций. трансформаторы должны быть включены в схему замещения электрической сети.

Заметно, что даже такая простая сеть, состоящая всего из двух пиний и двух трансформаторов, в схеме замещения содержит зна­чительное количество параметров, и проводить по ней расчет режима достаточно сложно.

Для упрощения расчетов без применения ЭВМ используют более простые схемы замещения с расчетными нагрузками под-i станций (рис. 6.8, в).

Рассмотрим процесс вычисления расчетных нагрузок подстан­ций с разными типами трансформаторов. В случае двухобмоточного трансформатора (подстанция 2) приводим мощность нагруз­ки S_2h, заданную на стороне низшего напряжения, с учетом по­терь мощности в обмотках 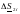к стороне высшего напряжения

Так как к данному расчету величины напряжений на стороне [высшего и низшего напряжений подстанций неизвестны расчет потерь мощности 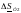ведем по номинальному напряжению сети

A-1-2

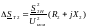(6.32)

Теперь с учётом холостого хода трансформатора 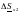и половины зарядной мощности

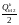
Линии 1-2, связанной с подстанцией 2, определяем расчётную нагрузку подстанции

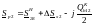(6.33)

Здесь расчет зарядной мощности также осуществляется по но­минальному напряжению линии

(6,34)

Таким образом, расчетная нагрузка подстанции включает саму мощность нагрузки подстанции, заданную на стороне низшего напряжения подстанции, потери мощности в обмотках трансформатора, потери холостого хода в нем и половину зарядной мощности линии, примыкающей к данной подстанции.

Рассмотрим последовательность вычисления расчетной на­грузки для подстанции / с трехобмоточным трансформатором.

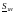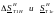Сначала по нагрузкам, заданным на стороне низшего и среднего S_lс напряжения подстанции, и по номинальному напря­жению сети рассчитываются потери мощности в соответствую­щих обмотках трансформатора и Д£_т1с- Затем вычисляют

мощности в начале этих обмоток

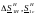
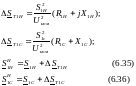
Из первого закона Кирхгофа применительно к точке О находят мощность в конце обмотки высшего напряжения

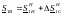(6,37)

Как и для других обмоток, определяют потери мощности и мощность в начале обмотки высшего напряжения:

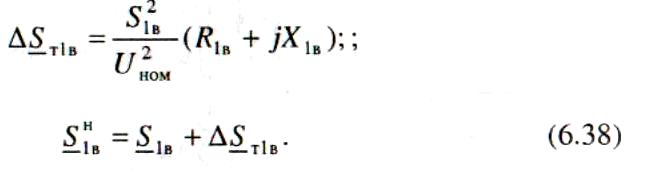
И, наконец, с учетом потерь холостого хода трансформатора и зарядных мощностей линий, связанных с подстанцией 1, вычис­ляют расчетную мощность подстанции