2.8 Задача 8. Расчет на прочность при совместном действии изгиба и кручения
Задача
8. Шкив с диаметром D1
и ветвями ремня, направленными вертикально,
вращается с угловой скоростью w
и передает мощность P (рисунок 15). Два
других шкива имеют одинаковый диаметр
D2
и ветви ремня, направленные горизонтально;
каждый из шкивов передает мощность P/2.
Требуется: а) определить моменты M1
и M2,
приложенные к шкивам; б) построить эпюру
крутящего момента T; в) определить
окружные усилия Ft1
и Ft2
на шкивах; г) определить давления на вал
F1
и F2,
принимая их равными трем окружным
усилиям; д) определить опорные реакции
от действия вертикальной силы F1
и построить эпюру изгибающего момента
в вертикальной плоскости Mвер;
е) определить опорные реакции от действия
горизонтальных сил F2
и построить эпюру изгибающего момента
в горизонтальной плоскости Mгор;
ж)построить эпюру суммарного изгибающего
момента Mизг;
к) найти опасное сечение и определить
по третьей теории прочности значение
максимального расчетного момента; и)
определить из расчета на прочность
диаметр вала при [
]
= 200 МПа.
Данные взять из таблицы 8.
Таблица 8
Вари-ант |
P, кВт |
w, рад/с |
a, м |
b, м |
c, м |
D1, м |
D2, м |
1 |
10 |
10 |
1.1 |
1.1 |
1.1 |
1.1 |
1.1 |
2 |
15 |
7.5 |
1.2 |
1.2 |
1.2 |
1.2 |
1.2 |
3 |
20 |
8 |
1.3 |
1.3 |
1.3 |
1.3 |
1.3 |
4 |
25 |
16 |
1.4 |
1.4 |
1.4 |
1.4 |
1.4 |
5 |
30 |
30 |
1.5 |
1.5 |
1.5 |
1.5 |
1.5 |
6 |
36 |
18 |
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
7 |
40 |
25 |
0.6 |
0.6 |
0.6 |
0.6 |
0.6 |
8 |
44 |
40 |
0.7 |
0.7 |
0.7 |
0.7 |
0.7 |
9 |
50 |
50 |
0.8 |
0.8 |
0.8 |
0.8 |
0.8 |
10 |
60 |
50 |
1.0 |
1.0 |
1.0 |
1.0 |
1.0 |
Указания. Задача относится к теме «Совместное действие изгиба и кручения». По условиям задачи требуется определить из расчета на прочность диаметр вала, для чего следует воспользоваться условием прочности при совместном действии изгиба и кручения, которое в случае круглого поперечного сечения по форме совпадает с условием прочности при изгибе. Входящий в это условие расчетный момент определяется с учетом изгибающего и крутящего моментов.
Пример
8.
Решить задачу 6 при следующих числовых
данных: P
= 80 кВт,
= 80 кВт, a
= b
= c
= d
= 1 м, [
]
= 100 МПа. Схема показана на рисунке 16 а.
Решение. Определяем моменты на шкивах
кН·м,
кН·м.
Строим эпюру крутящего момента, приведенную на рисунке 16 б.
Определяем окружные усилия на шкивах
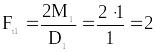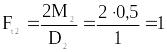кН,
кН.
Находим силы давления шкивов на вал
кН,
кН.
Опорные реакции в вертикальной плоскости (рисунок 16 в) определяем, исходя из уравнений равновесия
,
.
Получаем
кН,
кН.
Эпюра Mвер приведена на рисунке 16 г.
Опорные реакции в вертикальной плоскости (рисунок 16 д) определяем, исходя из уравнений равновесия
,
.
Получаем
кН,
.
Эпюра Mгор приведена на рисунке16 е.
Эпюру суммарного изгибающего момента строим (рисунок 16 ж), определяя его по формуле
.
В рассматриваемом случае очевидно, что опасным сечением является сечение A; максимальный расчетный момент здесь
кН·м.
Из условия прочности
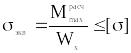
найдем осевой момент сопротивления
м3.
Так как для круглого сечения
,
то
м = 71,5 мм.
Округляя, окончательно имеем d = 72 мм.