Г. Типовые динамические звенья

К типовым относятся динамические звенья, описываемые дифференциальными уравнениями не выше второго порядка.

Позиционные звенья. К этому типу относятся динамические звенья, в которых выходная величина y(t) и ее производные зависят только от изменения входной величины x(t).

Б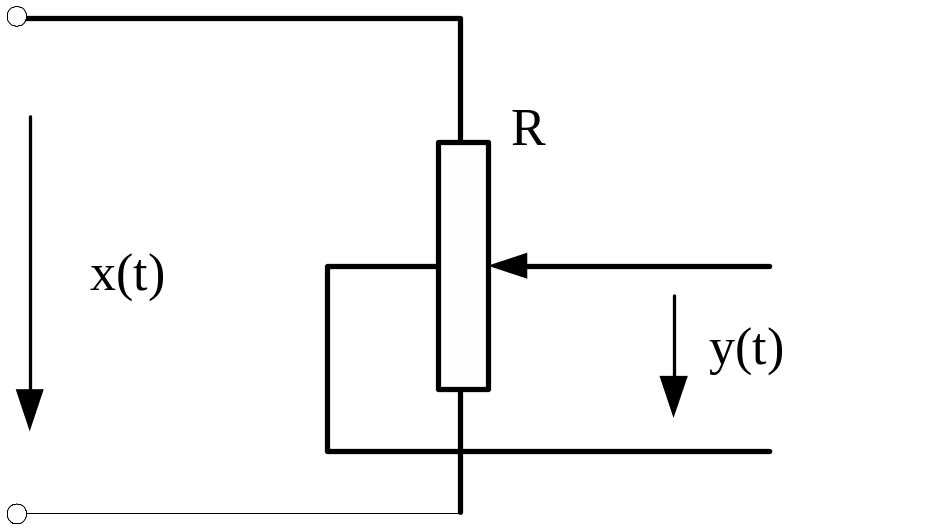 езынерционное звено является простейшим позиционным звеном, для него y(t)=kx(t). Примером такого звена является выходное напряжение, снимаемое с потенциометра. Передаточная функция

Частотная передаточная функция

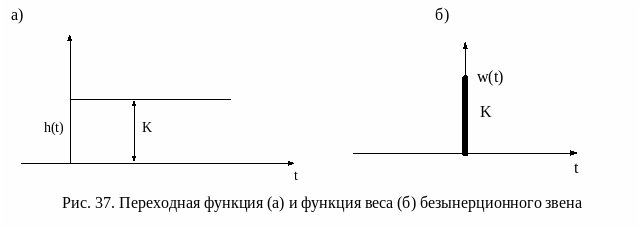
Апериодическое звено 1^го порядка. Дифференциальное уравнение для такой цепи может быть записано в алгебраизированной форме (Ts+1)y(t)=k(x(t). Передаточная функция записывается в виде W(p) = . В этих выражениях Т представляет постоянную апериодического звена, k – коэффициент передачи.

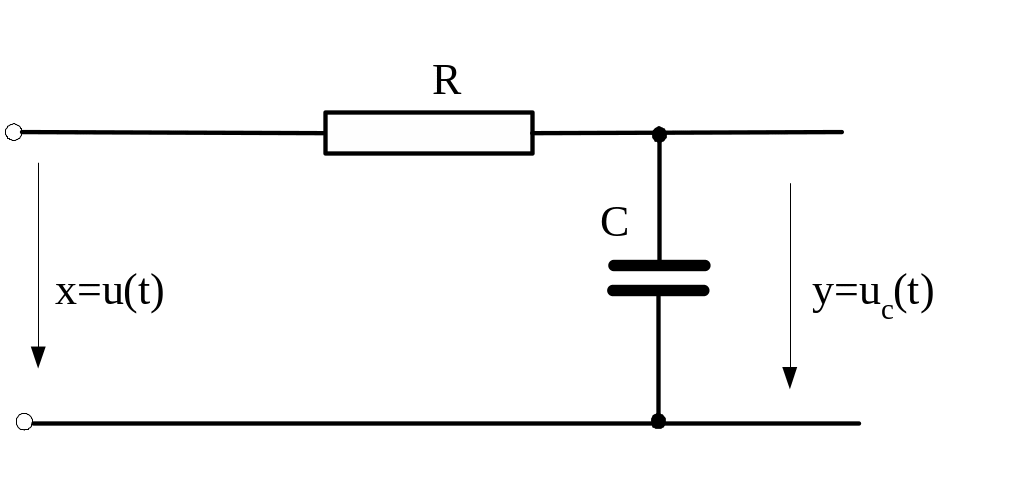
Простейшим примером такого звена является RC-цепь, если в качестве входной величины рассматривать входное напряжение u(t), а в качестве выходной – напряжение на емкости u_c(t). По второму закону Кирхгофа

u(t)=iR+u_c; параметрическое уравнение емкости i=C , заменив ток получаем

u(t)=CR +u_c

или в алгебраизированной форме: x(t) = (Ts+1)y(t), где Т=CR.

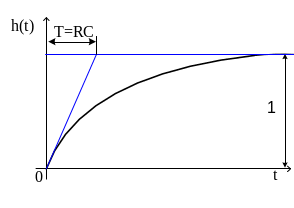
Ниже приведены характеристика апериодического звена 1-го порядка.

h(t)= ;

Рис. 39. Переходная функция и функция веса для апериодического звена 1-го порядка

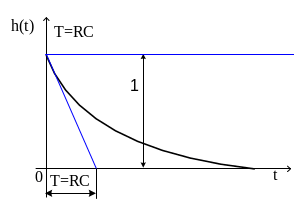
Рис. 40. Амплитудно-фазовая и логарифмическая амплитудно-частотная характеристики апериодического звена 1-го порядка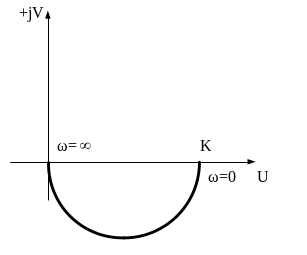

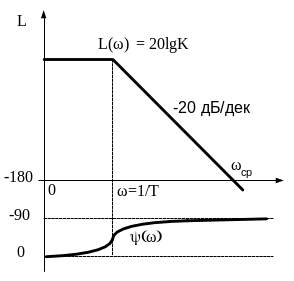
Передаточная и частотная передаточная функции апериодического звена 1-го порядка -,

Колебательное звено 2^го порядка. Примером такого звена может служить RLC-цепь при определенных соотношениях параметров. Уравнение такой цепи

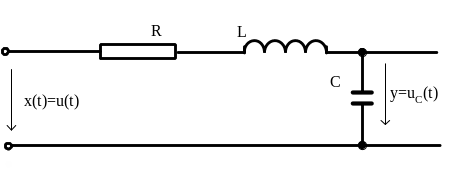
Передаточная функция этого звена ,

где ; ; ; .

Самостоятельная работа. Сформулировать условие, при котором последовательная RLC-цепь может представлять колебательное звено 2-го порядка.

Амплитудно-фазовая и логарифмическая амплитудно-частотная характеристики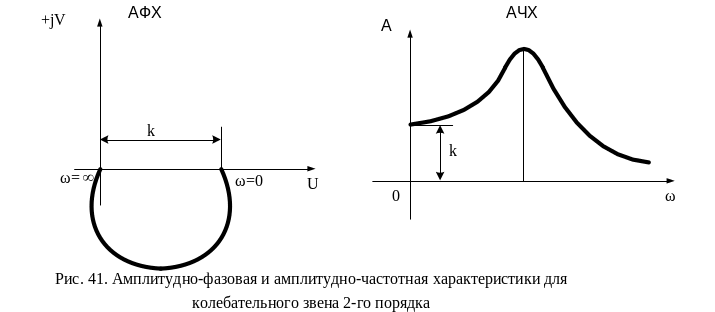

1. Устойчивость систем автоматического управления а. Общие понятия об устойчивости

При разработке и анализе устройств автоматического управления и регулирования важным фактором является способность системы сохранять свою работоспособность при различных возмущающих воздействиях. Если система под воздействием внешних возмущающих воздействий или при изменении с течением времени параметров каких либо элементов перестает нормально функционировать, то говорят о потере устойчивости системы, такая система не может быть применена в практических целях. Поэтому одна из первых задач, которую решают при создании автоматических устройств, это определение ее устойчивости.

Устойчивость – способность системы возвращаться в исходный режим или близкий к нему при выходе из него из него вследствие воздействия на неё.

Система устойчива, если её функция веса w(t) меньше любого, наперед заданного числа С

Рис.43. Функции веса для неустойчивой (а) и устойчивой (б) автоматических систем

Рассмотрим условия, при которых автоматическая система управления будет устойчивой. Пусть в алгебраизированной форме дифференциальное уравнение системы будет иметь вид зависимости выходной величины y(t) от задающего воздействия z(t)

, ,

Характеристическое уравнение, описывающее поведение системы в переходном процессе для такой системы будет

(*)

Учитывая, что все переменные в рассматриваемых уравнениях рассматриваются как отклонения от установившегося режима, то условием устойчивости будет

Решение характеристического уравнения может быть записано в виде

.

В общем случае корни характеристического уравнения могут быть либо вещественными, либо комплексно-сопряженными. Обозначим p_k=a_k+jb_k, где a_k и b_k –вещественная и мнимая часть корня p_k.

Для устойчивости САУ необходимо и достаточно, чтобы все вещественные части корней характеристического уравнения (*) были отрицательными.

Примеры расположения корней характеристического уравнения для разных случаев устойчивости приведены на рис. 44.

Рассмотренный метод определения устойчивости обладает тем недостатком, что определение корней характеристического уравнения (*) в случае высокого порядка этого уравнения не всегда представляется возможным. В связи с этими были разработаны критерии, позволяющие определить устойчивость системы без нахождения корней характеристического уравнения.

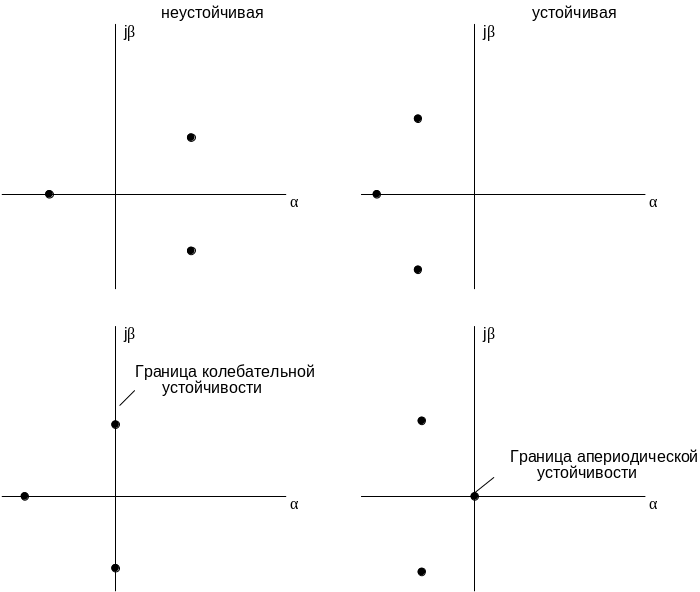
Рис. 44. Примеры оценки устойчивости по расположению корней характеристического уравнения