2.5. Методи інтерполяції
Досить часто необхідно побудувати прогноз для значень показників якого-небудь ряду усередині періоду спостережень (на ретроспективному інтервалі). Для відносно невеликої кількості точок часового ряду (до 10) як таку тенденцію, що не має властивості строгої монотонності, може бути підібрана функція у вигляді полінома відповідного ступеня. Коефіцієнти для цих поліномів знаходяться за допомогою методу інтерполяції. Дані поліноми (їх називають інтерполяційними) можуть бути представлені в різних формах (у формі Ньютона, у формі Лагранжа і т. д.). Особливість інтерполяційного полінома полягає в тому, що значення часового ряду (так звані вузлові точки) точно лежать на поліноміальній кривій.
Задачу екстраполяції можна вирішувати за допомогою цього методу, не віддаляючись особливо від границь ретроспективного інтервалу, тобто для одержання короткострокових прогнозів. Проте, незважаючи на ці недоліки, метод прогнозування на основі інтерполяційного полінома може бути використаний як перше наближення наявної залежності в інших, більш складних, методах і задачах.
Розглянемо сутність інтерполяції. Нехай на відрізку [а;b] задані (п + 1) опорних вузлових точок
а < х0 < х1 < ... < хп < b...
Нехай, крім того, задані п + 1 дійсних чисел уj (j = 0, ..., n), де уj - значення деякої функції f(x) у вузлових точках.
Завдання інтерполяції полягає в тому, щоб знайти такий багаточлен Jп(х) ступеня не більше п, в якому Jn(xj) = yj, j = 0,..., п.
Інтерполяція застосовується головним чином тоді, коли щодо функції f відомі тільки дискретні значення функції у = f(x). Щоб обчислити значення
цієї функції в інших внутрішніх точках відрізка [а; b] (інтерполяція) чи за межами відрізка вузлових точок (екстраполяція), її наближають багаточленом Jn(х), причому необхідне виконання умов
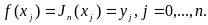(2.1)
Багаточлен, що задовольняє співвідношенням, даним в умовах (2.1), існує тільки один. Його можна представити в різних формах.
Розглянемо інтерполяційний багаточлен Лагранжа. Його можна представити такою формулою:
(2.2)
Очевидно, що множники Lj(x) задовольняють рівностям Lj(xj) = 1, Lj(xk) = 0 при k ≠ j. Отже, Jn(xj) = yj.
Приклад 2.1. Відомі такі дані про функцію (табл. 2.2).
Побудувати інтерполяційний багаточлен Лагранжа третього ступеня.
Таблиця 2.2
Вихідні значення функції у вузлах
j |
0 |
1 |
2 |
3 |
xi |
4 |
6 |
8 |
10 |
yi |
1 |
3 |
8 |
20 |
Таким чином, одержали поліном третього ступеня, який можна використовувати для прогнозування. Підставляючи в модель значення х, можна одержати значення у = J(x).
Особисті завдання.
Описати особливості методів простої екстраполяції (припущення, обмеження, загальній вигляд, найпростіші прийоми).
Описати особливості «наївних» екстраполяційних моделей.
Описати особливості екстраполяційних моделей на основі середньої. Обгрунтувати можливість застосування цього методу до даних таблиці контрольного завдання. Знайти довірчий інтервал, що враховує тільки ту невизначеність, що зв'язана з оцінкою середньої величини, а також довірчий інтервал, що враховує загальну дисперсія, зв'язану як з коливанням вибіркової середньої, так і з варіюванням індивідуальних значень навколо середньої.
Застосувати підхід, що формує прогнозну оцінку від фактично досягнутого рівня за допомогою середнього абсолютного приросту, до даних таблиці контрольного завдання (обгрунтувати, зробити висновки).
Застосувати метод двох крайніх точок до даних таблиці контрольного завдання (обгрунтувати, зробити висновки).
Застосувати метод середніх групових точок до даних таблиці контрольного завдання (обгрунтувати, зробити висновки).
Застосувати метод екстраполяції на основі темпу зростання до даних таблиці контрольного завдання (обгрунтувати, зробити висновки).
Застосувати метод інтерполяції (побудувати інтерполяційний багаточлен Лагранжа третього ступеня) до даних таблиці контрольного завдання (обгрунтувати, зробити висновки).
Контрольні завдання для студентів:
1. В таблиці 1 приведені дані про витрати споживачів на купівлю одягу. Використовуючи описані вище методи прогнозування, складіть прогноз витрат на купівлю одягу на кожний перший квартал наступного року (до 2005 р. включно).
Таблиця 1 - Споживацькі витрати на купівлю одягу, 2001 -2004 р. (грн)
Рік |
Квартал 1 |
Квартал 2 |
Квартал 3 |
Квартал 4 |
2001 |
3034 |
3284 |
3486 |
4831 |
2002 |
3077 |
3327 |
3458 |
4768 |
2003 |
3068 |
3358 |
3507 |
4657 |
2004 |
3043 |
3274 |
3452 |
4699 |
2. В таблиці 2 наводяться дані про щоденний обсяг продажів у супермаркеті «Антал» за останні чотири тижні.
Таблиця 2 - Обсяг продажу у супермаркеті «Антал»
Період (Тиждень/День) |
Обсяг продажів, тис грн. |
|
||||
1 тиждень тиждень |
2 тиждень |
3 тиждень |
4 тиждень тиждень |
|
||
Понеділок |
26 |
27 |
24 |
26 |
||
Вівторок |
З0 |
24 |
29 |
25 |
||
Середа |
27 |
24 |
30 |
27 |
||
Четвер |
24 |
29 |
26 |
27 |
||
П'ятниця |
30 |
34 |
32 |
30 |
||
Субота |
44 |
40 |
40 |
36 |
||
Неділя |
40 |
39 |
37 |
34 |
||
Використовуючи описані вище методи прогнозування, складіть прогноз обсягу продажів у супермаркеті «Антал» на кожний наступний понеділок (до 5-го тижня включно).
3. У таблиці 3 наведені обсяги реалізації хлібобулочних виробів за 4 роки.
Таблиця 3 - Обсяг реалізації хлібобулочних виробів, тис.т
Місяць
|
Рік |
|
|||
2001 |
2002 |
2003 |
2004 |
||
1 |
2 |
3 |
4 |
5 |
|
1 |
5,3 |
5,4 |
5,5 |
6,4 |
|
2 |
5,4 |
5,6 |
5,7 |
6,7 |
|
3 |
6,2 |
6,0 |
5,9 |
6,9 |
|
4 |
6,4 |
6,6 |
6,7 |
7,3 |
|
5 |
7,0 |
7,2 |
7,5 |
7,7 |
|
6 |
7,5 |
7,7 |
8,0 |
8,2 |
|
7 |
8,0 |
8,1 |
8,5 |
8,7 |
|
8 |
8,5 |
8,6 |
8,8 |
9,1 |
|
9 |
8,9 |
9,0 |
9,2 |
9,5 |
|
10 |
8,3 |
8,5 |
9,0 |
9,1 |
|
11 |
8,0 |
8,3 |
8,6 |
8,4 |
|
12 |
7,5 |
7,9 |
8,3 |
8,0 |
|
Використовуючи описані вище методи прогнозування, складіть прогноз обсягів реалізації хлібобулочних виробів на січень кожного наступного року (до 2005-го включно).
4. В таблиці 4 приведені дані про витрати споживачів на купівлю продуктів першої необхідності. Використовуючи описані вище методи прогнозування, складіть прогноз витрат на купівлю продуктів на кожний перший квартал наступного року (до 2013 р. включно).
Таблиця 4 - Споживацькі витрати на купівлю продуктів, 2009 -2012 р. (грн)
Рік |
Квартал 1 |
Квартал 2 |
Квартал 3 |
Квартал 4 |
2009 |
3024 |
3254 |
3466 |
3831 |
2010 |
3167 |
3317 |
3418 |
3668 |
2011 |
3268 |
3354 |
3502 |
3655 |
2012 |
3243 |
3374 |
3450 |
3691 |
5. В таблиці 5 наводяться дані про щоденний обсяг продажів у ТРЦ «Фабрика» за останні чотири тижні.
Таблиця 5 - Обсяг продажу у ТРЦ «Фабрика
Період (Тиждень/День) |
Обсяг продажів, тис грн. |
|
||||
1 тиждень тиждень |
2 тиждень |
3 тиждень |
4 тиждень тиждень |
|
||
Понеділок |
35 |
37 |
34 |
37 |
||
Вівторок |
40 |
34 |
39 |
34 |
||
Середа |
37 |
34 |
40 |
37 |
||
Четвер |
35 |
39 |
36 |
38 |
||
П'ятниця |
40 |
44 |
42 |
40 |
||
Субота |
54 |
50 |
50 |
46 |
||
Неділя |
50 |
49 |
47 |
45 |
||
Використовуючи описані вище методи прогнозування, складіть прогноз обсягу продажів у ТРЦ «Фабрика» на кожний наступний понеділок (до 5-го тижня включно).
6. У таблиці 3 наведені обсяги реалізації хлібобулочних виробів Херсонським хлібозаводом №1 за 4 роки.
Таблиця 6 - Обсяг реалізації хлібобулочних виробів, тис.т
Місяць
|
Рік |
|
|||
2009 |
2010 |
2011 |
2012 |
||
1 |
2 |
3 |
4 |
5 |
|
1 |
4,2 |
4,2 |
4,6 |
5,4 |
|
2 |
4,5 |
4,6 |
4,8 |
5,7 |
|
3 |
5,2 |
5,0 |
4,9 |
5,9 |
|
4 |
5,4 |
5,6 |
5,7 |
6,3 |
|
5 |
5.9 |
6,2 |
6,5 |
6,7 |
|
6 |
5,5 |
6,7 |
7,0 |
7,2 |
|
7 |
7,0 |
7,1 |
7,5 |
7,7 |
|
8 |
7,5 |
7,5 |
7,8 |
8,1 |
|
9 |
7,9 |
8,1 |
8,2 |
8,5 |
|
10 |
7,3 |
7,6 |
8,0 |
8,1 |
|
11 |
7,0 |
7,3 |
8,6 |
7,6 |
|
12 |
6,6 |
7,1 |
7,3 |
7,1 |
|
Використовуючи описані вище методи прогнозування, складіть прогноз обсягів реалізації хлібобулочних виробів Херсонським хлібозаводом №1 на січень кожного наступного року (до 2013-го включно).
7.В таблиці 7 приведені дані про витрати споживачів на купівлю м’ясних продуктів. Використовуючи описані вище методи прогнозування, складіть прогноз витрат на купівлю продуктів на кожний перший квартал наступного року (до 2013 р. включно).
Таблиця 7 - Споживацькі витрати на купівлю м’ясних продуктів, 2009 -2012 р. (грн)
Рік |
Квартал 1 |
Квартал 2 |
Квартал 3 |
Квартал 4 |
2009 |
2045 |
3251 |
2462 |
2822 |
2010 |
2163 |
2318 |
2418 |
2668 |
2011 |
2267 |
2353 |
2502 |
2655 |
2012 |
2242 |
2273 |
2451 |
2692 |
8. В таблиці 8 наводяться дані про щоденний обсяг продажів у ТЦ «АВТ» за останні чотири тижні.
Таблиця 8 - Обсяг продажу у ТЦ «АТВ»
Період (Тиждень/День) |
Обсяг продажів, тис грн. |
|
||||
1 тиждень тиждень |
2 тиждень |
3 тиждень |
4 тиждень тиждень |
|
||
Понеділок |
16 |
27 |
25 |
16 |
||
Вівторок |
21 |
25 |
29 |
15 |
||
Середа |
27 |
24 |
21 |
17 |
||
Четвер |
26 |
28 |
16 |
18 |
||
П'ятниця |
30 |
34 |
22 |
20 |
||
Субота |
35 |
30 |
30 |
26 |
||
Неділя |
30 |
29 |
27 |
26 |
||
Використовуючи описані вище методи прогнозування, складіть прогноз обсягу продажів у ТЦ «АТВ» на кожний наступний понеділок (до 5-го тижня включно).
9. У таблиці 9 наведені обсяги реалізації хлібобулочних виробів Херсонським хлібозаводом №2 за 4 роки.
Таблиця 6 - - Обсяг реалізації хлібобулочних виробів, тис.т
Місяць
|
Рік |
|
|||
2009 |
2010 |
2011 |
2012 |
||
1 |
2 |
3 |
4 |
5 |
|
1 |
5,1 |
5,5 |
5,5 |
6,5 |
|
2 |
5,5 |
5,6 |
5,6 |
6,8 |
|
3 |
6,3 |
6,1 |
5,8 |
6,9 |
|
4 |
6,4 |
6,6 |
6,7 |
7,2 |
|
5 |
7,1 |
7,3 |
7,4 |
7,7 |
|
6 |
7,4 |
7,6 |
8,0 |
8,2 |
|
7 |
8,1 |
8,1 |
8,5 |
8,6 |
|
8 |
8,5 |
8,5 |
8,8 |
9,1 |
|
9 |
8,8 |
9,1 |
9,1 |
9,5 |
|
10 |
8,4 |
8,5 |
9,0 |
9,2 |
|
11 |
8,0 |
8,4 |
8,5 |
8,4 |
|
12 |
7,6 |
8,0 |
8,4 |
8,1 |
|
Використовуючи описані вище методи прогнозування, складіть прогноз обсягів реалізації хлібобулочних виробів Херсонським хлібозаводом №2 на січень кожного наступного року (до 2013-го включно)