2.2. Метод двох крайніх точок

У ряді випадків при відсутності достатньої кількості даних (напри­клад, кількість точок ряду менше 5) для простого прогнозу можна ви­користовувати метод прогнозування по прямій, проведеній через дві крайні точки. Недоліком цьо­го методу є припущення про лінійний характер тенденції зміни показ­ника в часі, що не завжди так, і низька якість оцінок параметрів моделі.

Розглянемо сутність методу прогнозування на основі прямої, про­веденої через дві крайні точки. З упорядкованої вибірки беруть дві крайні точки (х₁, у₁) і (х_n, у_п) і через них проводять пряму вигляду у = а₀ + а_гх. Оцінки параметрів обчислюються за формулами:

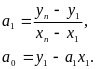(2.3)

Отримані в такий спосіб оцінки є незміщеними, але вони не будуть переконливими і тим більше ефективними.

Схема методу пояснюється на рис. 2.1.

Рис. 2.1. Метод двох крайніх точок

Приклад 2.2. Відома динаміка прибутку підприємства за період 1990 — 1998 pp. (тис. грн) (табл. 2.3).

Таблиця 2.3

Динаміка прибутку підприємства

Роки	1990	1991	1992	1993	1994	1995	1996	1997	1998
xj	0	1	2	3	4	5	6	7	8
yj	44,8	50,5	48,6	40,2	16,6	10,2	14,6	22,0	24,8

Знайдемо оцінки параметрів моделі:

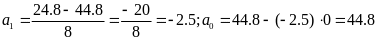
Таким чином, модель має вигляд .

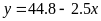2.3. Метод середніх групових точок

Цей метод є узагальненням попереднього. Метод полягає в тому, що дану сукупність розбивають на дві чи три приблизно рівні частини, а потім знаходять координати середніх точок для крайніх груп.

Нехай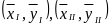 — координати середніх точок для крайніх груп. Тоді оцінки лінійної моделі a₀ , а₁ обчислюються за формулами, аналогічними формулі (2.3):

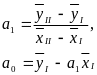(2.4)

Оцінки, отримані цим методом, є незміщеними і переконливими, але неефективними.

Приклад 2.3. Використовуючи вихідні дані приклада 2.2, знайдемо оцінки параметрів моделі а₀ і а₁ , розбивши попередньо вибірку на дві частини.

І група - дані з 1990 по 1993 pp.

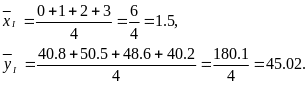
II група - дані з 1994 по 1998 pp.

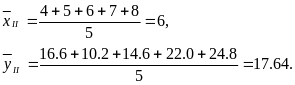
Використовуючи формули (2.4), знаходимо параметри моделі

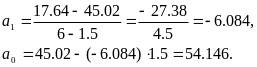
Таким чином, модель має вигляд y = 54,146 - 6,084x;.

Порівнюючи параметри для двох лінійних моделей, побудованих різ­ними методами, можна переконатися в істотному розходженні оцінок параметрів. Отримана друга модель більш точна і краща. Вона може бути використана для простого прогнозу.

2.4. Прогнозування на основі темпів зростання

У ряді випадків для одержання відносно простого прогнозу за рядами, що мають явно виражений нелінійний монотонний характер зростання чи спаду, використовується метод екстраполяції на основі темпу зростання.

Ланцюгові темпи зростання розрахову­ються за формулою 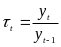. Якщо ланцюгові темпи зростання утворять строго монотонно зростаючу послідовність, тобто кожне наступне значення буде більше попереднього, то як модель кривої зростання варто вибирати нелінійну монотонну функцію (експонентну чи ступеневу залежність, функцію Гомперца чи логістичну криву). Якщо ж ланцюгові темпи зростання не утворять монотонної послідовності, тобто наступні значення для однієї частини ряду будуть більше, а для іншої - менше поперед­ніх, то як модель тренду можна брати поліноміальну, чи гармонійну, функцію. Якщо ланцюгові темпи зростання менше 1, це свідчить про зменшення поточного значення ряду в порівнянні з попереднім. Якщо ж ланцюгові темпи зростання більше 1,- про збільшення поточного значення ряду в порівнянні з попереднім.

Ланцюговий темп приросту визначається на основі абсолютних приростів і обчислюється за такою формулою: 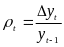, де абсолютні прирости .

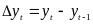При нескладному перетворенні даної формули одержуємо вираз, що зв’язує темп приросту і темп зростання, тобто

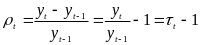
Темпи приросту можуть бути і позитивними, і негативними. Для економічного аналізу темпи приросту зручно розраховувати у відсотках. Так, наприклад, якщо ланцюговий темп приросту склав 5%, це означає, що поточне значення ряду y_t зменшилося в порівнянні з колишнім рівнем y_t-1 на 5%. І, навпаки, позитивні ланцюгові темпи приросту означають збільшення поточного значення в порівнянні з попереднім.

Найкращий результат цей метод дає у випадку рядів, що мають експонентний характер, де ланцюгові темпи зростання і приросту показників постійні. Якщо знати аналітичне вираження функції, то можна розрахувати миттєві (безупинні) темпи приросту за такою формулою:

.

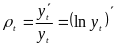Значення миттєвих темпів приростів будуть відрізнятися від їх дискретних значень, це пов'язано з величиною Δt, чим вона менше, тим менше розходження.

Розглянемо приклад використання прогнозу ряду на основі темпу зростання.

Дано деякий експонентний ряд, що заданий табличними значеннями (табл. 2.4) і у вигляді аналітичної функції y_t = 2e^0.5t. Необхідно визначити абсолютні ланцюгові прирости, ланцюгові темпи зростан­ня, ланцюгові темпи приростів і розрахувати середній темп зростання.

Таблиця 2.4 Табличні значення функції y_t = 2e^0.5t

t	yt	Δyt	τt	ρt
1	3,2924	-	-	-
2	5,42	2,1276	1,6462	0,6462
3	8,9224	3,5024	1,6462	0,6462
4	14,6882	5,7658	1,6462	0,6462
5	24,1798	9,4916	1,6462	0,6462
6	39,8050	15,6202	1,6462	0,6462
7	65,5273	25,7223	1,6462	0,6462
8	107,8716	42,3443	1,6462	0,6462
9	177,5790	69,7074	1,6462	0,6462
10	292,332	114,753	1,6462	0,6462

Розрахуємо ланцюгові абсолютні прирости за формулою Δy_t = y_t -y_t-1 . Знаючи аналітичну формулу, можна знайти вираз для абсолютних приростів, тобто Δy_t = 2e^0.5t – 2e^0.5(t-1) = 2e^0.5(t-1)(e^0.5-1) .

Аналіз динаміки абсолютних приростів показує нелінійну тенденцію збільшення показника у у часі.

Розрахуємо ланцюгові темпи зростання за формулою .

Знаючи аналітичну формулу, можна знайти вираження для темпів зростання, тобто .

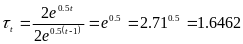Ланцюгові темпи зростання є величиною постійною для експонентної функції.

Розрахуємо ланцюгові темпи приросту за формулою . Підставляючи дані, одержимо такий вираз:

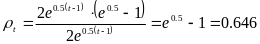
Аналогічно темпи приросту:

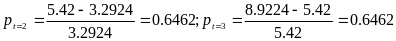і т. д.

Якщо відомо аналітичне представлення функції, то можна розрахувати миттєві темпи приросту: 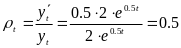. Як видно, спостерігається значне відхилення миттєвих темпів приростів від їх дискретних значень.

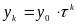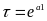Очевидно, що для експонентного ряду можна одержати формулу для прогнозу поточного рівня у_k у залежності від відомого значення темпу зростання т і початкового рівня ряду y₀. Так, , де - темп зростання експонентного ряду, вираженого формулою .

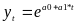Випадки, коли фактичний ряд показників представлений експонентною залежністю, досить рідкі, тобто розрахункові значення темпів зростання для реальних рядів можуть відрізнятися більшим чи меншим чином. Наприклад, якщо представлені значення ряду, в основі якого лежить експонентна функція, заміряні з деякою похибкою, то фактичні темпи зростання не будуть строго рівні між собою, але очевидно, що зазначені значення будуть зосереджені поблизу деякого рівня - теоретичного темпу зростання ряду. Тому у більш загальному випадку роблять вирівнювання вихідного ряду за експонентним законом, ґрунтуючись на деякому початковому значенні і середньому темпі приросту.