Лабораторна робота 1 прості методи прогнозування

Мета заняття: Отримати відомості про прості методи прогнозування і навички роботи з цими методами на основі елементів часового ряду. Навчитися основним прийомам розрахунків.

План

1. Методи простої екстраполяції.

2. Метод двох крайніх точок.

3. Метод середніх групових точок.

4. Прогнозування на основі темпів зростання.

5. Методи інтерполяції.

1. Методи простої екстраполяції

Методи простої екстраполяції засновані на при­пущенні

• про практично незмінний характер процесу, що протікає,

• про відсутність істотних змін у стані зовнішнього і внутрішнього середови­ща об'єкта прогнозування.

Це накладає певні обме­ження на можливості використання цих методів: для одержання оперативних і короткострокових про­гнозів в умовах неповної інформації.

Операцію екстраполяції в загальному вигляді можна представити як визначення значення функції:

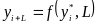
де yi+L — значення рівня, що екстраполюється;

L — період попередження;

уi* — рівень, прийнятий за базу екстраполяції.

Існують різні найпростіші прийоми екстраполяції, серед яких

1. метод побудови «наївної моделі»;

2. метод екстраполяції на основі середньої;

3. метод екстраполяції на основі середнього темпу зростання;

4. екстраполяція на основі лінійного тренда, побудованого по двох крайніх точках чи двох середніх групових точках;

5. екстрапо­ляція на основі інтерполяційних багаточленів;

1.«Наївні» екстраполяційні моделі використовують у ряді випадків у прогностичних дослідженнях, коли будується прогноз у припу­щенні абсолютної незмінюваності значень попередніх рівнів у май­бутньому. Цю модель для ряду y_t можна записати в такому вигляді:

y_t = y_t-1 ,(t = 2, 3, ..., п).

Якщо розглядається сталість приростів, яку по­значимо u_t = y_t- y_t_₁, то модель буде така: u_t = u_t-1 ,(t = 3, 4, ..., п).

2. Екстраполяція на основі середньої використовується для одержання прогнозу в припущенні незмінюваності в майбутньому середніх значень попередніх рівнів. Середній рівень ряду не повинен мати тенденції до зміни або ця зміна повинна бути незначною. У цьому випадку можна прийняти, що прогнозований рівень дорівнює середньому значенню рівнів у минулому, тобто

.

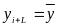Довірчі границі для середньої при невеликому числі спостережень і припущенні про нормальний закон розподілу визначаються в такий спосіб:

,

де t_α — табличне значення t-статистики Стьюдента з n- 1 ступенями свободи й рівнем імовірності р, — середня квадратична по­милка середньої. Це значення визначається за такою формулою:

,

де s — середнє квадратичне відхилення для вибірки (незміщена оцінка).

Значення її визначається за формулою:

.

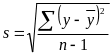Довірчий ін­тервал, отриманий як формула враховує ту невизначеність, що зв'язана з оцінкою середньої величини. Застосування довірчого інтер­валу дозволяє перейти від точкового прогнозу до інтервального і тому збільшує точність отриманої прогностичної оцінки за припущення про те, що прогнозований показник дорівнює середній, тобто при такому підході не враховується те, що окремі значення досліджуваного показника варіювали навколо серед­ньої в минулому і, безсумнівно, будуть варіювати й у майбутньому. У зв'язку з цим довірчий інтервал для прогностичної оцінки повинен враховувати і цей фактор. Таким чином, загальна дисперсія, зв'язана як з коливаністю вибіркової середньої, так і з варіюванням індивідуальних значень навколо середньої, складе . Отже, довірчі інтервали для прогностичної оцінки дорівнюють:

Недоліком даного методу прогнозування є те, що довірчий інтервал не повинен бути зв'язаний з періодом попередження - в економіці вкрай рідко спостерігаються статистичні сукупності даних, що мають стійкий характер.

3. Підхід, що формує прогнозну оцінку від фактично досягнутого рівня за допомогою середнього абсолютного приросту. Відповідно до нього прогноз на к кроків уперед на момент часу t = N + k виходить за формулою:

де САП - середній абсолютний приріст.

Цей спосіб привертає увагу багатьох працівників статистичних орга­нів завдяки своїй простоті і легкості реалізації. Однак, крім зазначених достоїнств, він має кілька істотних недоліків.

По-перше, усі фактичні спостереження є результатом закономірності і випадковості, отже, «відштовхуватися» від останнього спостереження неправомірно.

По-друге, немає можливості оцінити правомірність використання середнього приросту в кожному конкретному випадку.

По-третє, даний підхід не дозволяє сформувати інтервал, усередину якого попадає прогнозована величина, і визначити ступінь впевненості в цьому.

У зв'язку з цим даний підхід застосовується лише як орієнтир майбутнього розвитку чи у випадку, якщо неможливо використовувати описувані нижче статистичні методи (наприклад, при дуже малому обсязі спостережень).